非参数密度估计：核密度估计器详解

"文档介绍了核密度估计器的概念，特别是其中的核函数，包括均匀、高斯和epi-等，并强调了核密度估计器在非参数密度估计中的应用，以解决直方图存在的问题。" 在统计学和机器学习领域，核密度估计（Kernel Density Estimation, KDE）是一种常用的技术，用于估计数据分布的密度函数。它是非参数方法的一种，不像参数方法那样假设数据遵循特定的固定结构，而是利用所有数据点来构建估计。这种灵活性使得核密度估计在处理未知或复杂分布时特别有用。 直方图是估计数据分布的最直观方法，但存在一些缺点。首先，直方图依赖于人为设定的bin宽度，不同的bin大小会显著影响最终的分布形状。其次，直方图的边界选择也会影响结果，导致不连续和阶梯状的分布估计。为了解决这些问题，核密度估计应运而生。 核密度估计的基本思想是在每个数据点处放置一个核函数（kernel function），然后将所有核函数的加权和进行积分，以得到整个数据集的连续密度估计。核函数的选择至关重要，常见的核函数有均匀核、高斯核（也称为高斯窗口）和epi-核等。均匀核适用于简单的分布，而高斯核因其平滑性和良好的数学特性而广泛应用，它能产生平滑的密度估计曲线，减少了对bin宽度和边界选择的敏感性。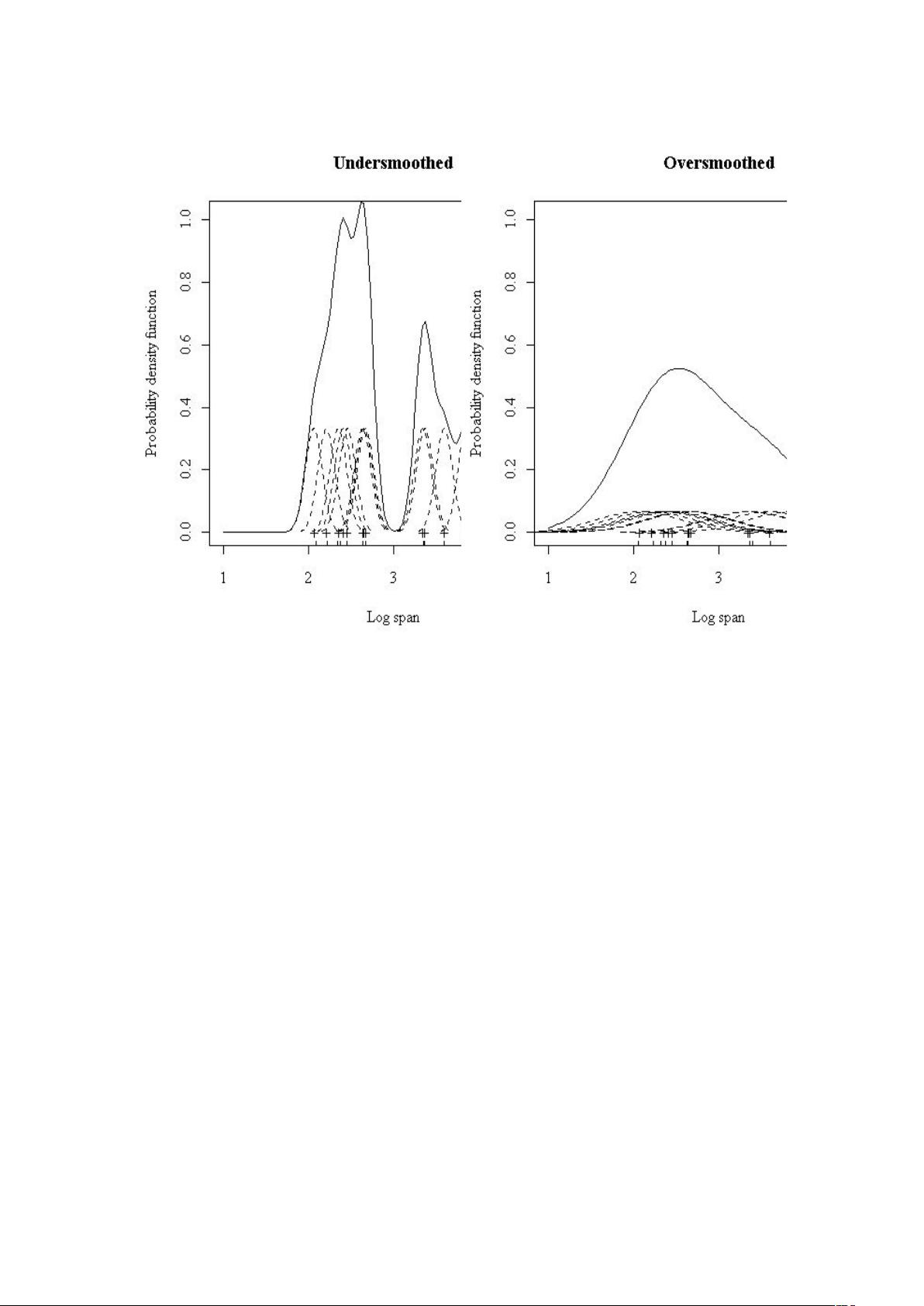 高斯核通常表示为一个标准正态分布，其形状由带宽（bandwidth）参数控制，带宽决定了核函数在数据点周围的影响范围。合适的带宽值可以确保估计的密度既不过于平滑，丢失细节，也不过于粗糙，引入噪声。带宽的选择是一个关键步骤，可以通过多种方法确定，如Silverman's rule of thumb、Scott's normal reference rule等经验规则，或者采用更复杂的数据驱动方法，如交叉验证。 除了高斯核，还有其他核函数可供选择，例如Epanechnikov核，它在中心区域具有较大的权重，而在远离中心的地方快速减小，这有助于减少边缘效应。此外，还可以使用三角核、指数核等，每种核函数都有其特定的适用场景和优缺点。 核密度估计提供了一种强大的工具来估计数据的连续概率密度，克服了直方图的局限性，尤其适合于处理小样本或分布形状复杂的数据。在实际应用中，通过选择合适的核函数和带宽，我们可以获得更加准确和直观的分布描述，这对于数据探索、模型选择和预测分析都有着重要的作用。