二维热传导有限元的波前法MATLAB实现与解析

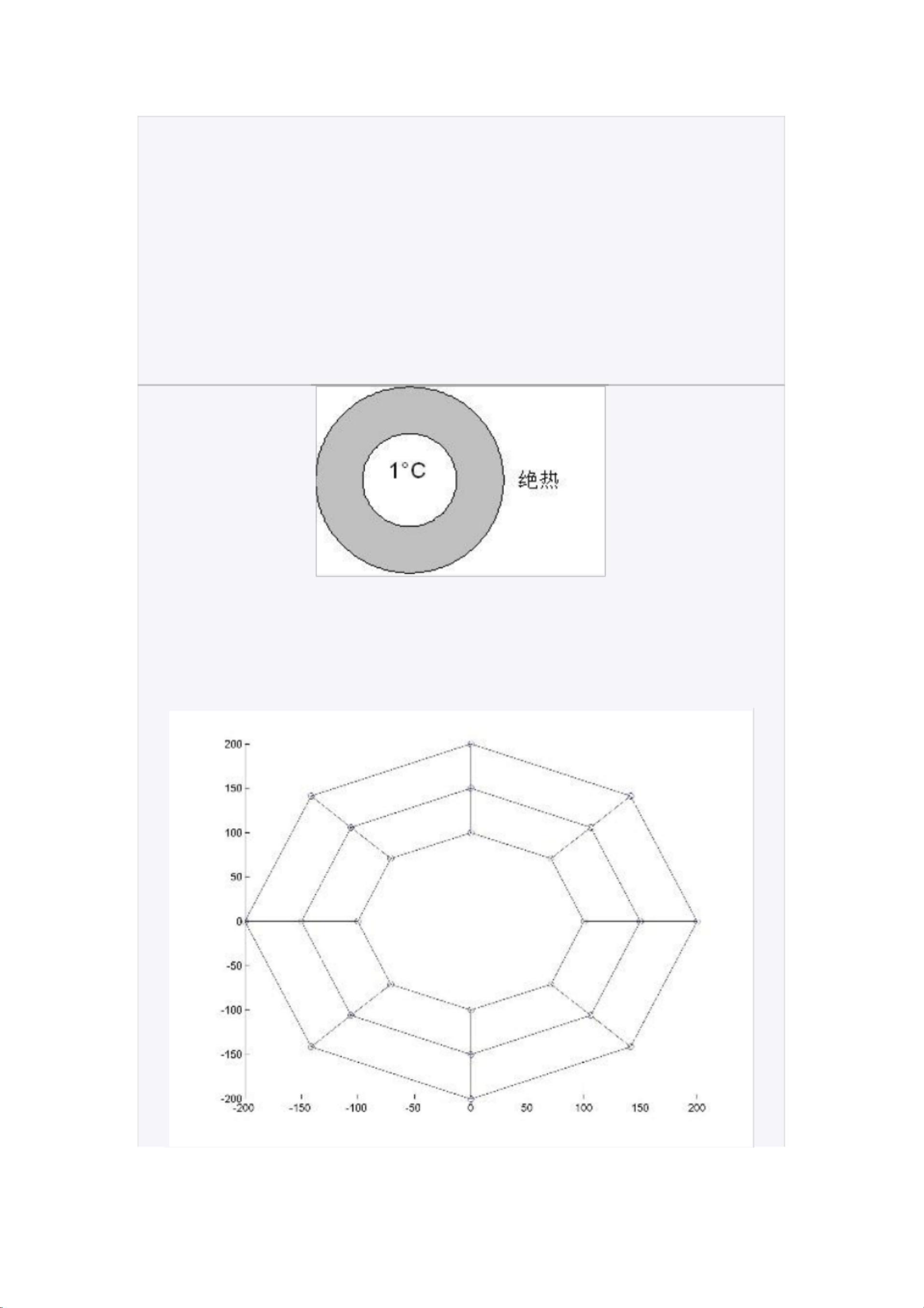
该资源是一份关于波前法及其在MATLAB中实现的PDF文档，主要探讨了二维热传导问题的有限元分析，包括波前法的基本概念、算法以及MATLAB程序实现。文档中提到了波前法的历史，以及作者在理解和实现波前法过程中遇到的挑战。 波前法是一种求解大型线性方程组的有效方法，特别适用于有限元分析中的数值计算。它由B.M.Irons于1970年提出，随着时间的发展，这种方法已经发展出了多种变体。文档中引用了Pascal JOLY的著作来阐述波前法的基本原理，但未提供具体的程序代码或详细讨论。作者强调，尽管有算法指导，但实现波前法的程序仍然具有相当的难度。 在实现波前法之前，作者首先构建了一个用于解决二维热传导问题的MATLAB有限元程序。二维热传导问题可以由以下微分方程描述： \[ \frac{\partial}{\partial x}(K_x \frac{\partial T}{\partial x}) + \frac{\partial}{\partial y}(K_y \frac{\partial T}{\partial y}) = -q \] 其中，\( T \) 表示温度，\( K_x \) 和 \( K_y \) 分别是x和y方向的热传导系数，而 \( q \) 是热源。为了将此微分方程转换为有限元方程，需要进行一系列数学处理，包括离散化、边界条件的应用以及线性系统的构建。 文档中提到，作者在深入研究并教授有限元方法后，才真正理解了如何从二阶偏微分方程导出有限元表达式。这通常涉及Galerkin方法、变分原理以及选择合适的基函数来构建弱形式。在MATLAB中，可以利用其强大的矩阵运算功能来实现这些步骤。 波前法在效率上与高斯消去法进行了比较，它通过逐步推进的方式解决方程，减少了计算中的存储需求和计算量，特别是在大规模问题中表现优越。然而，理解和实现波前法需要深刻理解数值线性代数和有限元理论。 这份文档旨在为对波前法感兴趣的人提供一个基础，帮助他们理解波前法的基本思想，以及如何在MATLAB环境中实现二维热传导问题的有限元分析。对于希望深入研究有限元方法和高效求解线性方程组的读者，这是一个有价值的参考资料。