动态规划实战：斐波那契与SPU/LMP算法详解

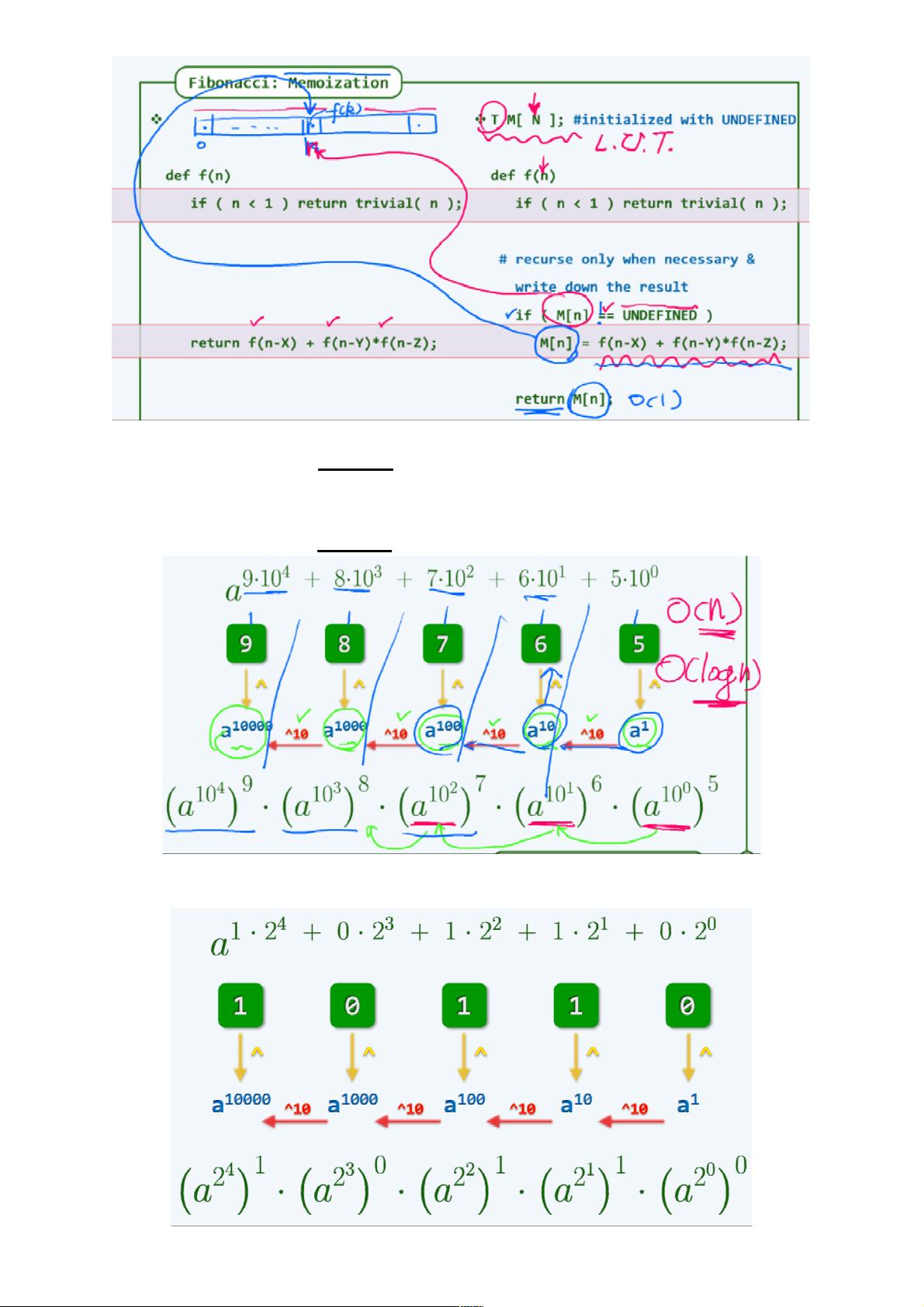
动态规划是计算机科学中一种强大的算法设计技术，用于解决具有重叠子问题和最优子结构的问题。在这个主题中，我们探讨了几个关键的动态规划概念和应用。 首先，我们从斐波那契数列(Fibonacci)开始，这是递归和记忆化搜索（Memoization）的典型例子。递归方法通过函数自身调用来计算数列的值，但当问题规模增大时，它的时间复杂度呈指数级增长，如在计算fib(45)和更大值时效率显著下降。记忆化搜索通过预先存储已计算的结果避免重复计算，显著提高了效率，特别是对于 fib(64)和fib(100)这类大值的求解。 接下来是求幂运算（Power），这是一种基础的动态规划应用。通常，我们可以用二进制表示法来优化计算，将幂次分解为二进制位数，从而将时间复杂度降低到O(r)，其中r是幂次的位数。然而，这个理想化的O(logn)复杂度在实际操作中可能并不现实，因为计算机硬件的限制意味着即使在理想情况下，四则运算也并非瞬间完成。 SPU（Shortest Path Upward）是一种在图论中的动态规划方法，用于找到从起点到顶点的最短路径，适用于上滤矩阵。LMP（Longest Manhattan Path）则涉及在网格中找到最长的曼哈顿距离路径，这种问题也可以通过动态规划策略解决，通常与LCS（Longest Common Substring，最长公共子串）类似，后者可以通过动态规划的两种形式（DeAC和DiAC）来求解。 0/1背包问题（0-1 Knapsack）是经典的动态规划问题之一，涉及在给定容量限制下选择物品以最大化价值。最后，传递闭包（Transitive Closure）关注的是确定一个关系是否具有传递性，并提供相应的算法定义和实现。 全对最短路径（All-Pair Shortest Path，APSP）是动态规划在图论中的另一个高级应用，它寻找图中任意两个节点之间的最短路径。这些算法展示了动态规划如何在各种问题中找到最优解决方案，同时强调了时间和空间复杂度优化的重要性。 总结来说，第3周-3B-动态规划内容涵盖了递归、记忆化、图论中的路径问题、背包问题以及关系理论，展示了动态规划在解决一系列问题中的核心价值和策略。理解并掌握这些概念和技巧对于提升算法设计能力至关重要。