平面几何证明技巧：点共线与线共点的证明方法

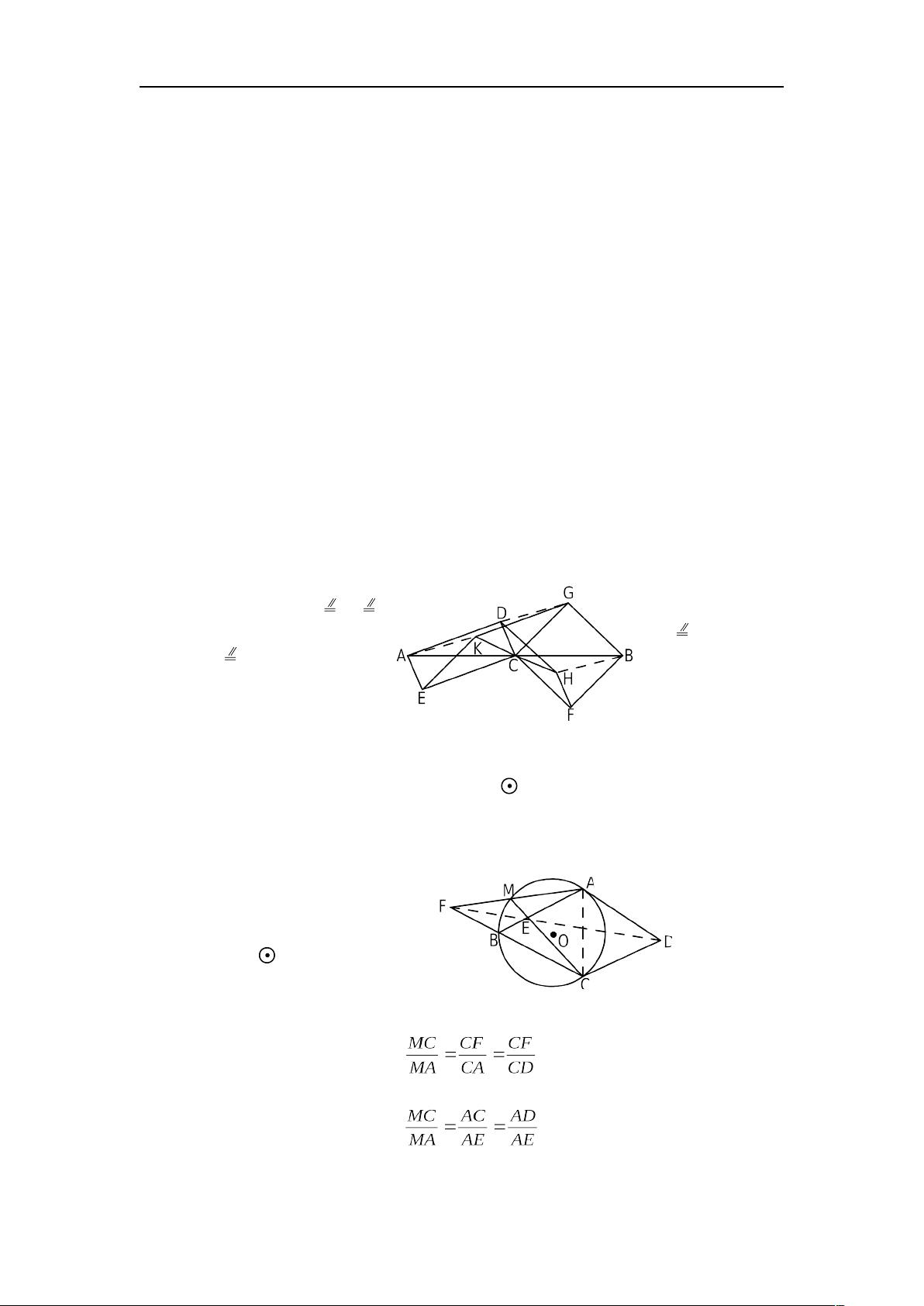
"本资源主要涉及点共线和线共点的证明方法，以及在几何问题中的应用。通过具体的例子，介绍了如何利用邻补角关系、平行四边形性质、相似三角形等几何原理来证明点共线和线共点。同时，提到了梅涅劳斯定理和塞瓦定理在解决此类问题中的应用。" 在平面几何中，点共线和线共点是基础且重要的概念。点共线意味着三个或多个点处于同一直线上，而线共点则是指多条直线经过同一个点。理解这些概念有助于我们解决复杂的几何问题。 首先，证明点共线常见的方法有以下几种： 1. **邻补角关系**：如果三个点所形成的两个角是邻补角，那么这三个点共线。 2. **连线必过第三点**：证明两点的连线也经过第三个点，即三点构成的三角形的面积为零。 3. **平行线性质**：若三个点构成的三角形的两边平行，那么第三边也与之平行，因此三点共线。 例如，在例1中，通过构造平行四边形AECD和BFCG，证明了H，C，K三点共线。利用平行四边形的性质，即对边平行，可以推出AK和DG、AK和HB都平行，进而证明四边形AHBK是平行四边形，其对角线AB和KH互相平分，由于C是AB的中点，所以KH必过点C，从而得出K，C，H三点共线。 在例2中，利用菱形的性质和相似三角形原理，证明了D，E，F三点共线。关键在于找出三角形之间的相似关系，通过角度对应相等，得出比例关系，最后利用平行线性质证明∠ADF=∠DFB，从而证明三点共线。 例3中，涉及圆的性质和切线的特性。通过构造B，C，M，P四点共圆，可以得出∠PMC=∠ABC，进一步推导出C，D，Q，M四点也共圆。利用圆周角定理和圆的幂定理，证明了P，E，F三点共线。 在解决这类问题时，**梅涅劳斯定理**和**塞瓦定理**是非常有用的工具。梅涅劳斯定理指出，在三角形ABC中，如果直线d分别与边AB、BC、CA相交于点D、E、F，那么有AD/DB × BE/EC × CF/FA = 1。塞瓦定理则描述了关于三角形外接圆的切线和交点的特殊关系。不过在上述例子中，它们并未直接应用，但了解这些定理对于更复杂问题的解决是有帮助的。 理解和掌握点共线和线共点的证明方法，能帮助我们更好地解决平面几何问题，同时也为深入学习几何学的其他高级定理打下坚实的基础。通过实例分析和练习，我们可以提高自己的几何思维能力和逻辑推理能力。