搜索策略概览：从盲目到启发式

"本章主要探讨搜索策略在解决IT问题中的应用，特别是针对存在代价的图搜索和启发式搜索。内容涵盖了盲目搜索、启发式搜索、与/或树搜索以及博弈树的启发式搜索，强调了搜索在不良结构或非结构化问题中的重要性，并按照是否使用启发式信息及问题表示方式进行分类。" 在IT领域，搜索策略是解决问题的关键工具，尤其适用于那些结构复杂或者信息不完全的问题。本章的焦点在于如何在各种搜索策略中选择合适的路径以达到最优解。 1. **搜索概念**：搜索是基于现有知识和经验，通过不断探索可能的解决方案，以最小代价找到问题答案的过程。这适用于不良结构或非结构化问题，以及复杂度较高的问题，即使理论上存在算法，也可能因问题规模而变得难以处理。 2. **盲目搜索**，如**广度优先搜索 (BFS)** 和**深度优先搜索 (DFS)**，它们不依赖于问题的具体信息，而是遵循预设的控制策略。BFS通常用于找到最短路径，而DFS则适用于内存限制或寻找特定路径的情况。 3. **代价一致搜索**考虑了边上的代价，确保在代价树中找到最低成本的路径。这种搜索策略通常结合BFS进行优化，例如Dijkstra算法或Bellman-Ford算法。 4. **启发式搜索**，包括**贪心算法**、**A算法**和**A*算法**，引入了问题相关的启发信息来指导搜索。贪心算法每次选择当前看起来最优的步骤，A算法结合了实际代价和预计代价，A*算法通过加入启发式函数进一步优化了A算法，提供了一种接近最优解的高效搜索方法。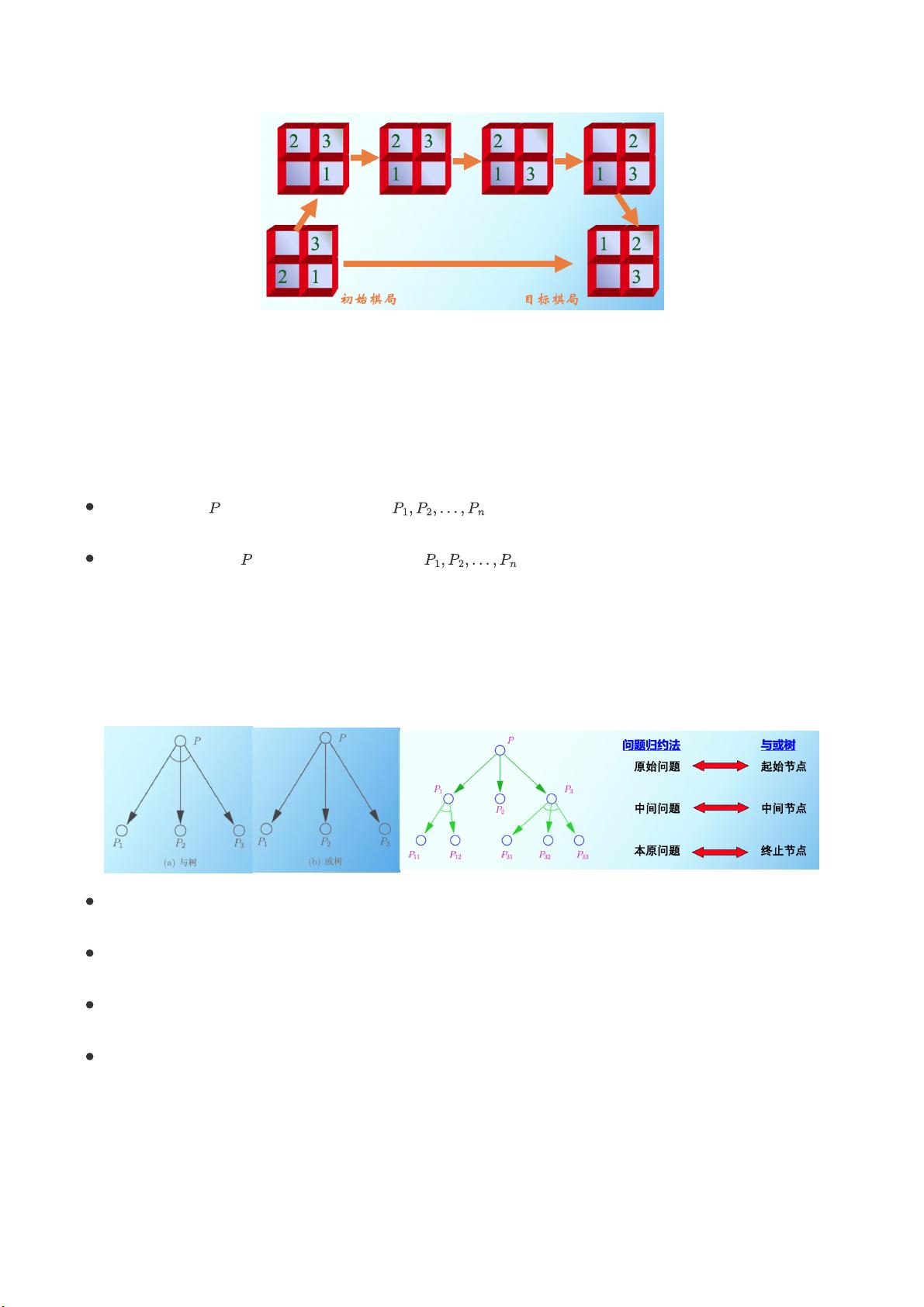 5. **与/或树搜索**是问题归约法的一种形式，适用于问题可以分解为子问题的情况。与/或树的搜索策略包括广度优先和深度优先，同时结合启发式搜索能有效减少搜索空间。 6. **博弈树的启发式搜索**在游戏AI中特别重要，如极大极小过程，用于评估对手可能的动作并进行剪枝，以减少搜索的复杂性。 7. **剪枝**是搜索策略中的一个重要概念，它通过消除明显无效的分支来优化搜索效率，防止无用的工作，例如Alpha-Beta剪枝在棋类游戏中广泛使用。 8. **问题的形式化**包括初始状态、后继函数、操作函数、路径耗散函数、目标测试函数以及问题的解，这些都是定义问题并实施搜索策略的基础。 9. **状态空间**是问题所有可能状态的集合，通过状态和操作之间的关系来描述问题。状态空间图以节点表示状态，边表示操作，有助于可视化和理解问题的结构。 搜索策略是IT问题解决中的核心工具，不同的搜索方法适应不同的问题特性，正确选择和应用这些策略能大大提高问题解决的效率和质量。在面对复杂问题时，理解并熟练运用这些搜索策略是至关重要的。