MATLAB中状态空间与传递函数转换实践

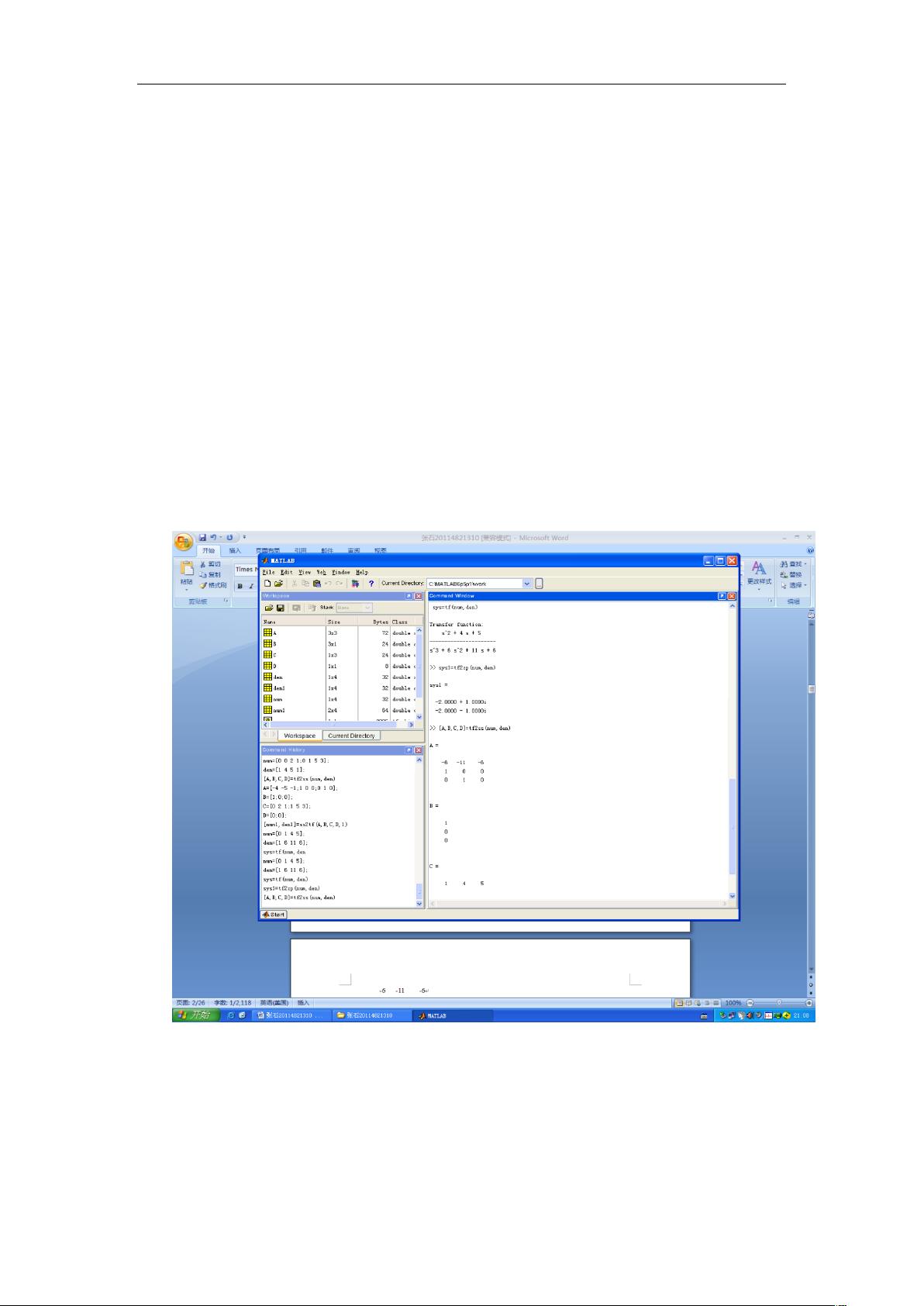
"本实验主要探讨了如何在MATLAB环境下将多变量系统的传递函数转换为状态空间表达式，以及反之的过程。实验旨在让学生熟悉状态空间模型的建立，掌握状态空间表达式与传递函数之间的相互转换，并熟练运用MATLAB的相关函数。 实验的核心在于理解和应用状态空间模型和传递函数的基本概念。状态空间表达式是一种描述系统动态行为的数学模型，通常表示为：x'(t) = Ax(t) + Bu(t)，y(t) = Cx(t) + Du(t)，其中x(t)是系统状态向量，u(t)是输入向量，y(t)是输出向量，A、B、C和D分别是系统矩阵。传递函数则是一种在复频域内描述系统响应的表达方式，G(s) = C(sI - A)^(-1)B + D，其中s是复频率，num(s)和den(s)分别代表传递函数的分子和分母多项式。 MATLAB提供了两个关键函数来处理这两种模型：`ss`函数用于创建状态空间模型，其语法为`sys = ss(A,B,C,D)`；而`tf`函数用于创建传递函数，其语法为`G = tf(num,den)`。此外，`tf2ss`函数可以将传递函数转换为状态空间模型，`ss2tf`函数则相反，将状态空间模型转换为传递函数。对于多输入系统，`ss2tf`函数需要指定输入编号iu。 实验步骤中，给出了一个传递函数G(s) = [2/s^3, 5/s^2, 3/s; 1/s^3, 4/s^2, 5/s, 1]，并利用`tf2ss`函数求得了对应的A、B、C、D矩阵，然后通过`ss2tf`函数验证了转换的正确性。计算结果显示，A矩阵为[-4 -5 -1; 1 0 0; 0 1 0]，B矩阵为[1; 0; 0]，C矩阵为[0 2 1; 1 5 3]，D矩阵为[0; 0]。 这个实验不仅加深了学生对多变量系统模型的理解，还强化了他们在MATLAB环境中的实际操作技能，为后续的控制系统设计和分析奠定了基础。通过这样的实践，学生能够更加灵活地运用不同模型来描述和处理复杂的系统问题。