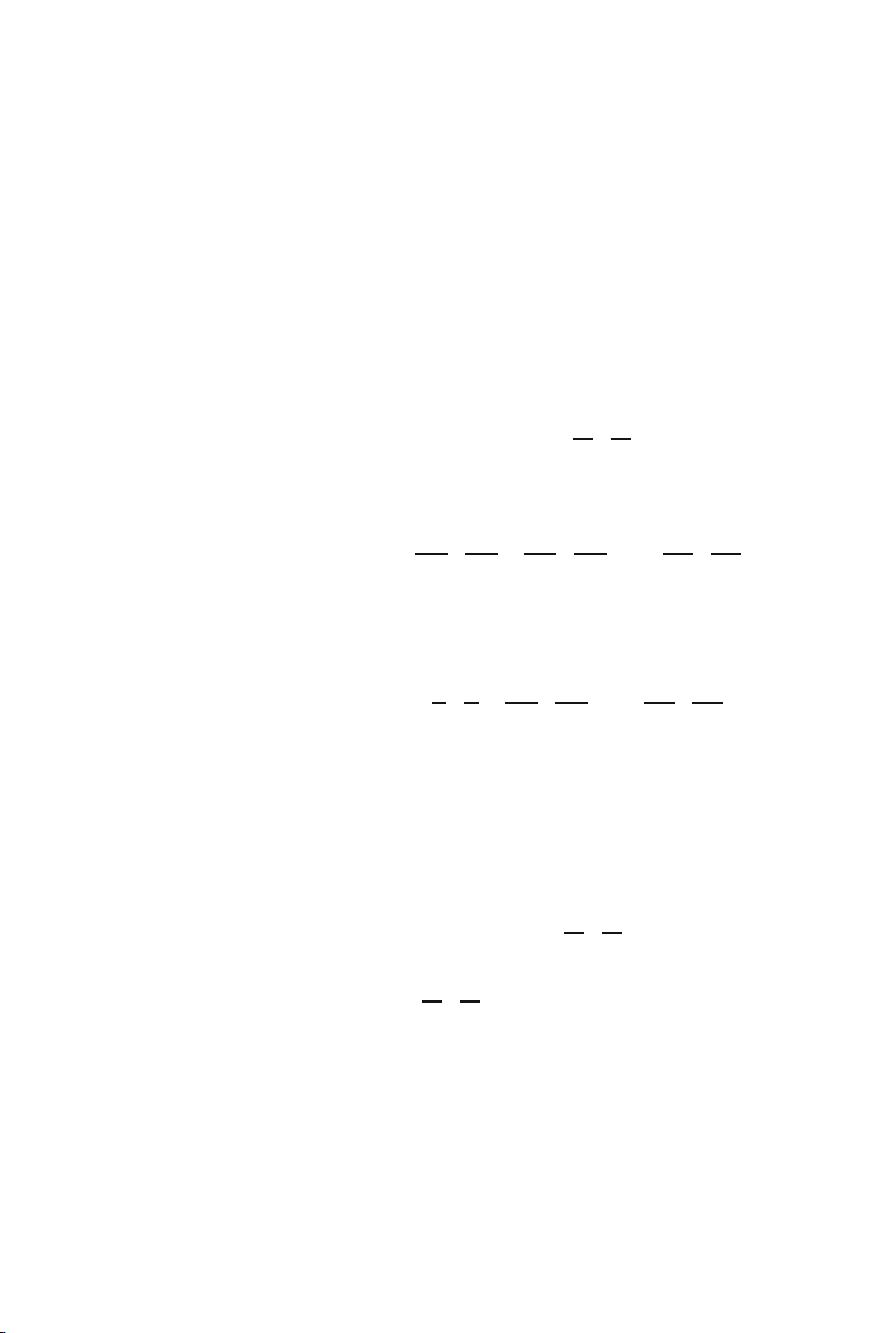李振宁等人2012年多项式优化近似方法综述

需积分: 0 125 浏览量更新于2024-07-17 收藏 734KB PDF 举报

《近似方法在多项式优化中的应用》是SpringerBriefs in Optimization系列的一部分，由赵静宁、何思迈和张书忠共同编著。该书专注于算法和理论技术的展示，以及在广泛优化领域的案例研究和实际应用。系列编辑包括帕诺斯·帕达洛斯（Panos M. Pardalos）、扬·迪特尔·平特（Janos D. Pinter）、斯蒂芬·罗宾逊（Stephen M. Robinson）和塔玛斯·特尔凯伊（Tamás Terlaky），以及My T. Thai，这些专家共同推动了优化理论和实践的发展。本书特别关注优化在应用数学、工程、医学、经济和其他应用科学中的不断增长的应用。它提供了一种深入理解多项式优化模型、算法和其在现实世界问题中的实用性的途径。作者们来自上海大学数学系的赵静宁、明尼苏达大学工业与系统工程系的张书忠以及香港城市大学管理科学系的何思迈，他们共同探讨了这一复杂领域的最新进展和技术。本书涵盖了以下几个核心主题： 1. **多项式优化模型**：阐述了如何构建和理解多项式优化问题，这些问题是基于多项式的目标函数和约束条件，广泛应用于各种优化场景中。 2. **算法设计与分析**：讨论了针对多项式优化问题的近似算法，如内点法、梯度方法、核化方法等，以及它们的收敛性和效率分析。 3. **理论基础**：介绍了多项式优化的理论框架，包括实数算术几何、李代数和动力系统理论，这些都是理解和解决此类问题的关键工具。 4. **实例与应用**：通过实际案例研究展示了多项式优化在诸如控制理论、机器学习、经济学和数据科学等领域的应用，强调了其在解决复杂决策问题中的价值。 5. **数值实验与评估**：书中可能包含了对不同算法在特定问题上的比较，以及通过实验验证理论结果的重要性。《近似方法在多项式优化中的应用》的出版号、国际标准书号(ISBN)和电子版ISBN以及DOI都提供了方便读者获取的详细信息，表明了这是一本具有深度和实用性的学术著作，旨在为优化领域的专业人士和学生提供一个全面的参考资源。

1.1 History 7

(SDP) relaxations of the given polynomial optimization problem in such a way

that the corresponding optimal values are monotone and converge to the optimal

value of the original problem. Thus it can in principle solve any instance of (PO) to

any given accuracy. For univariate polynomial optimization, Nesterov [88] showed

that the SOS method in combination with the SDP solution has a polynomial-time

complexity. This is also true for unconstrained multivariate quadratic polynomial

and bivariate quartic polynomial when the nonnegativity is equivalent to the SOS.

In general, however, the SDP problems required to be solved by the SOS method

may grow very large, and are not practical when the program dimension goes high.

At any rate, thanks to the recently developed efﬁcient SDP solvers (e.g., SeDuMi of

Sturm [109], SDPT3 of Toh et al. [112]), the SOS method appears to be attractive.

Henrion and Lasserre [49] developed a specialized tool known as GloptiPoly (the

latest version, GloptiPoly 3, can be found in Henrion et al. [50]) for ﬁnding a global

optimal solution of the polynomial optimization problems arising from the SOS

method, based on Matlab and SeDuMi. For an overview on the recent theoretical

developments, we refer to the excellent survey by Laurent [69].

Along a different line, the intractability of general polynomial optimization also

motivates the search for suboptimal, or more formally, approximate solutions. In the

case that the objective polynomial is quadratic, a well-known example is the SDP

relaxation and randomization approach for the max-cut problem due to Goemans

and Williamson [39], where essentially a 0.878-approximation ratio of the model

max

x∈{1,−1}

x is shown with F

F being the Laplacian of a given graph. Note that

the approach in [39] has been generalized subsequently by many authors, including

Nesterov [87], Ye [115, 116], Nemirovski et al. [86], Zhang [117], Charikar and

Wirth [23], Alon and Naor [5], Zhang and Huang [118], Luo et al. [74], and He et al.

[48]. In particular, when the matrix F

F is only known to be positive semideﬁnite,

Nesterov [87] derived a 0.636-approximation bound for max

x∈{1,−1}

x.For

general diagonal-free matrix F

F, Charikar and Wirth [23] derived an Ω(1/ lnn)-

approximation bound, while its inapproximate results are also discussed by Arora

et al. [7]. For the matrix ∞ → 1-norm problem max

x∈{1,−1}

y∈{1,−1}

y,Alon

and Naor [5] derived a 0.56-approximation bound. Remark that all these approx-

imation bounds remain hitherto the best available ones. In continuous polynomial

optimization, Nemirovski et al. [86] proposed an Ω(1/lnm)-approximation bound

for maximizing a quadratic form over the intersection of m co-centered ellipsoids.

Their models are further studied and generalized by Luo et al. [74] and He et al. [48].

Among all the successful approximation stories mentioned above, the objective

polynomials are all quadratic. However, there are only a few approximation results

in the literature when the degree of the objective polynomial is greater than two.

Perhaps the very ﬁrst one is due to De Klerk et al. [63] in deriving a PTAS of

optimizing a ﬁxed degree homogenous polynomial over a simplex, and it turns out

to be a PTAS of optimizing a ﬁxed degree even form (homogeneous polynomial

with only even exponents) over the Euclidean sphere. Later, Barvinok [14] showed

that optimizing a certain class of polynomials over the Euclidean sphere also

8 1 Introduction

admits a randomized PTAS. Note that the results in [14, 63] apply only when

the objective polynomial has some special structure. A quite general result is

due to Khot and Naor [59], where they showed how to estimate the optimal

value of the problem max

x∈{1,−1}

∑

1≤i, j,k≤n

ijk

with (F

ijk

) being square-

free, i.e., F

ijk

= 0 whenever two of the indices are equal. Speciﬁcally, they

presented a polynomial-time randomized procedure to get an estimated value that

is no less than Ω(



lnn

) times the optimal value. Two recent papers (Luo and

Zhang [76] and Ling et al. [72]) discussed polynomial optimization problems with

the degree of objective polynomial being four, and start a whole new research

on approximation algorithms for high degree polynomial optimization, which are

essentially the main subject in this brief. Luo and Zhang [76] considered quartic

optimization, and showed that optimizing a homogenous quartic form over the

intersection of some co-centered ellipsoids can be relaxed to its (quadratic) SDP

relaxation problem, which is itself also NP-hard. However, this gives a handle on

the design of approximation algorithms with provable worst-case approximation

ratios. Ling et al. [72] considered a special quartic optimization model. Basically,

the problem is to minimize a biquadratic function over two spherical constraints.

In [72], approximate solutions as well as exact solutions using the SOS method are

considered. The approximation bounds in [72] are indeed comparable to the bound

in [76], although they are dealing with two different models. Very recently, Zhang

et al. [120] and Ling al. [73] further studied biquadratic function optimization over

quadratic constraints. The relations with its bilinear SDP relaxation are discussed,

based on which they derived some data-dependent approximation bounds. Zhang

et al. [121] also studied homogeneous cubic polynomial optimization over spherical

constraints, and derived some approximation bound.

However, for (PO) with an arbitrary degree polynomial objective, the approx-

imation results remained nonexistent until recently. He et al. [46] proposed a ﬁrst

polynomial-time approximation algorithm for optimizing any ﬁxed degree homo-

geneous polynomial with quadratic constraints. This has set off a ﬂurry of research

activities. In a subsequent paper, He et al. [45] generalized the approximation meth-

ods and proposed ﬁrst polynomial-time approximation algorithm for optimizing any

ﬁxed degree inhomogeneous polynomial function over a general convex set. Note

that this is the only approximation result for optimizing any degree inhomogeneous

polynomial function. So [106] improved some of the approximation bounds in [45],

for the case of optimizing any ﬁxed degree homogeneous polynomial with spherical

constraints. Along a different line, He et al. [47] studied any degree polynomial

integer programming and mixed integer programming. In particular, they proposed

polynomial-time approximationalgorithms for polynomial optimization with binary

constraints and polynomial optimization with spherical and binary constraints. The

results of He, Li, and Zhang were summarized in the recent Ph.D. thesis of Li [70],

which forms a basis for this brief.

1.2 Contributions 9

1.2 Contributions

This brief presents a systematic study on approximation methods for optimizing any

ﬁxed degree polynomial function over some important and widely used constraint

sets, e.g., the Euclidean ball, the Euclidean sphere, hypercube, binary hypercube,

intersection of co-centered ellipsoids, a general convex compact set, and even

a mixture of them. The objective polynomial function ranges from multilinear

tensor function, homogeneous polynomial, and generic inhomogeneous polynomial

function. With combination of the constraint sets, the models constitute most of

the subclasses of (PO) in real applications. The detailed description of the models

studied is listed in Sect. 1.3.3, or speciﬁcally Table 1.1. All these problems are

NP-hard in general, and the focus is on the design and analysis of polynomial-

time approximation algorithms with provable worst-case performance ratios.

The application of these polynomial optimization models will be discussed.

Speciﬁcally, our contributions are highlighted as follows:

1. We propose approximation algorithms for optimization of any ﬁxed degree

homogeneous polynomial over the Euclidean ball, which is the ﬁrst such result

for approximation algorithms of polynomial optimization problems with an

arbitrary degree. The approximation ratios depend only on the dimensions of

the problems concerned. Compared with any existing results for high degree

polynomial optimization, our approximation ratios improve the previous ones,

when specialized to their particular degrees.

2. We establish key linkages between multilinear functions and homogeneous

polynomials, and thus establish the same approximation ratios for homogeneous

polynomial optimization with their multilinear form relaxation problems.

3. We propose a general scheme to handle inhomogeneous polynomial optimization

through the method of homogenization, and thus establish the same approxi-

mation ratios (in the sense of relative approximation ratio) for inhomogeneous

polynomial optimization with their homogeneous polynomial relaxation prob-

lems. It is the ﬁrst approximation bound of approximation algorithms for general

inhomogeneous polynomial optimization with a high degree.

4. We propose several decomposition routines for polynomial optimization over

different types of constraint sets, and derive approximation bounds for multi-

linear function optimization with their lower degree relaxation problems, based

on which we derive approximation algorithms for polynomial optimization over

various constraint sets.

5. With the availability of our proposed approximation methods, we illustrate some

potential modeling opportunities with the new optimization models.

The whole brief is organized as follows. In the remainder of this chapter

(Sects. 1.3 and 1.4), we introduce the notations and various polynomial optimiza-

tion models studied in this brief, followed by some necessary preparations, e.g.,

deﬁnitions of approximation algorithms and approximation ratios, various tensor

operations, etc. The main part of the brief is the dealing with approximation

10 1 Introduction

methods for the polynomial optimization models concerned, which will be the

contents of Chaps. 2 and 3. In particular, in Chap. 2, we elaborate on polynomial

optimization over the Euclidean ball: we propose various techniques step by step in

handling different types of objective polynomial functions, and discuss how these

steps leads to the ﬁnal approximation algorithm for optimizing any ﬁxed degree

inhomogeneous polynomial function over the Euclidean ball. Chapter3 deals with

various technical extensions of the approximation methods proposed in Chap. 2,

armed with which we propose approximation algorithms for solving many other

important polynomial optimization models. Sample applications of the polynomial

optimization models and their approximation algorithms will be the topic for

Chap. 4. Finally, in Chap. 5 we conclude this brief by tabulating the approximation

ratios developed in the brief so as to provide an overview of the approximation

results and the context; other methods related to approximation algorithms of

polynomial optimization models are also commented on, including a discussion of

the recent developments and possible future research topics.

1.3 Notations and Models

Throughout this brief, we exclusively use the boldface letters to denote vectors,

matrices, and tensors in general (e.g., the decision variable x

x, the data matrix Q

Q,and

the tensor form F

F), while the usual non-bold letters are reserved for scalars (e.g., x

being the ﬁrst component of the vector x

x, Q

being one entry of the matrix Q

Q).

1.3.1 Objective Functions

The objective functions of the optimization models studied in this brief are all

multivariate polynomial functions. The following multilinear tensor function (or

multilinear form) plays a major role in the discussion:

Function T F(x

,...,x

) :=

∑

1≤i

≤n

,1≤i

≤n

,...,1≤i

≤n

···i

···x

where x

∈ R

for k = 1,2,...,d; and the letter “T” signiﬁes the notion of tensor.

In the shorthand notation we denote F

F =(F

···i

) ∈R

×n

×···×n

to be a d-th order

tensor, and F to be its corresponding multilinear form. In other words, the notions

of multilinear form and tensor are exchangeable. The meaning of multilinearity is

that if one ﬁxes (x

,...,x

) in the function F, then it is a linear function in x

and so on.

Closely related with the tensor form F

F is a general d-th degree homogeneous

polynomialfunction f (x

x),wherex

x ∈R

. We call the tensor F

F =(F

···i

) supersym-

metric (see [64]), if any of its components F

···i

is invariant under all permutations

1.3 Notations and Models 11

of {i

,...,i

}. As any homogeneous quadratic function uniquely determines a

symmetric matrix, a given d-th degree homogeneous polynomial function f (x

x) also

uniquely determines a supersymmetric tensor form. In particular, if we denote a d-th

degree homogeneous polynomial function

Function H f(x) :=

∑

1≤i

≤i

≤···≤i

≤n



···i

···x

then its corresponding supersymmetric tensor can be written as F

F =(F

···i

) ∈R

with F

···i

≡ F



···i

/|Π(i

,...,i

)|,where|Π(i

,...,i

)| is the number of

distinctive permutations of the indices {i

,...,i

}. This supersymmetric tensor

representation is indeed unique. Let F be its corresponding multilinear form deﬁned

by the supersymmetric tensor F

F,thenwehavef (x

x)=F(x

x,x

x,...,x



 

). The letter “H”

here is used to emphasize that the polynomial function in question is homogeneous.

We shall also consider in this brief the following mixed form:

Function M f(x

,...,x

) := F(x

,...,x

  

,...,x

  

,...,x

  

where d

+ d

+ ···+ d

= d, x

∈R

for k = 1,2,...,s, d-th order tensor form F

F ∈

×n

×···×n

; and the letter “M” signiﬁes the notion of mixed polynomial form.

We may without loss of generality assume that F

F has partial symmetric property,

namely for any ﬁxed (x

,...,x

), F(·

·,·

·,...,·



 

,...,x

  

,...,x

  

) is a

supersymmetric d

th order tensor form, and so on.

Beyond the homogeneous polynomial functions (multilinear form, homogeneous

form, and mixed forms) described above, we also study in this brief the generic

multivariate inhomogeneous polynomial function. An n-dimensional d-th degree

polynomial function can be explicitly written as a summation of homogenous forms

in decreasing degrees as follows:

Function P p(x

x) :=

∑

k=1

x)+ f

∑

k=1

x,x

x,...,x



 

)+ f

where x

x ∈ R

, f

∈R,and f

x)=F

x,x

x,...,x



 

) is a homogenous form of degree k

for k = 1,2,...,d; and letter “P” signiﬁes the notion of polynomial. One natural way

to deal with inhomogeneous polynomial function is through homogenization;that

is, we introduce a new variable, to be denoted by x

in this brief, which is actually

set to be 1, to yield a homogeneous form

p(x

x)=

∑

k=1

x)+ f

∑

k=1

x)x

d−k

+ f

= f (

x),

剩余128页未读，继续阅读

rorowell

粉丝: 0
资源: 4

李振宁等人2012年多项式优化近似方法综述

Approximation with polynomial kernels and svm classifiers

Saddlepoint Approximation Methods in Financial Engineering

Calculator Function Approximation

integral_approximation = 0 for i in range(n): x_i = a + i * h integral_approximation += func(x_i) * h integral_approximation是什么

Use your program from Problem 7.8 and the forearm data to get a bootstrap confidence interval for the mean. Compare this to the theoretical one. Chapter 7:Monte Carlo Methods for Inferential Statistics

matlab PCE

Chi-squared approximation may be incorrect

sequential convex programming

Implement a Matlab function which completes the following task: Give the minimax approximation of a given function f on (a a closed interval; (b)a set of finitely many points.

Robbins-Monro setting

最新资源