CPM：光流与立体声匹配的精细从粗到细 PatchMatch 方法

149 浏览量更新于2024-08-29 收藏 1.05MB PDF 举报

"本文介绍了一种名为CPM（从粗到细PatchMatch）的匹配方法，该方法结合了有效的随机搜索策略和从粗到细的方案，以解决计算机视觉中的密集对应问题，特别针对光流和立体声匹配。受到最近邻域（NNF）算法的启发，CPM在保持效率的同时，通过引入传播步骤来限制随机搜索半径，从而减少了结果的噪声，提高了对应关系的平滑性。此外，CPM还能够捕捉到具有大运动的微小结构，这是传统从粗到细方法的挑战。与其他NNF技术相比，CPM在处理密集对应关系时表现更优，并且在MPI-Sintel和KITTI数据集上的光流结果优于最新方法，且运行速度更快。" 在深入探讨CPM方法之前，有必要先理解“粗匹配”和“精细匹配”的概念。粗匹配是首先快速寻找大致的对应关系，而精细匹配则是对这些初步结果进行优化，以获得更加精确的对应。在传统的从粗到细方法中，可能会丢失微小结构或在处理大运动时遇到困难。 CPM方法的核心在于其改进的随机搜索策略和全局正则化。随机搜索策略允许快速探索大量可能的对应，而传播步骤则确保了在不同层次间的对应关系的一致性，这在NNF技术中通常是缺失的。通过限制相邻层之间的搜索半径，CPM能够自然地产生平滑的对应关系，减少了不准确和噪声。这种方法特别适合处理密集的对应任务，因为它能够捕捉到即使在大运动背景下也保持一致的微小特征。为了进一步增强性能，CPM采用了边缘保留插值方法EpicFlow进行插值。EpicFlow是一种先进的光流估计技术，它能够保留图像边缘信息，使得流动估计更加准确。结合CPM，这种方法在实际应用中展现出优越的性能，特别是在MPI-Sintel和KITTI等标准数据集上，其不仅在精度上超越了当前的光流方法，而且在执行速度上也有显著优势。 "粗匹配的精细匹配"这篇文章提出了一种创新的匹配策略，通过结合随机搜索、从粗到细的层次结构和全局正则化，解决了密集对应中的关键挑战。这种方法对于光流和立体匹配等领域具有重要的实用价值，并且在实际应用中已经显示出优于现有技术的性能。

1051-8215 (c) 2016 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.

This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI 10.1109/TCSVT.2017.2720175, IEEE

Transactions on Circuits and Systems for Video Technology

Level 3

Level 2

Level 1

Level 0

Coarse to ﬁne

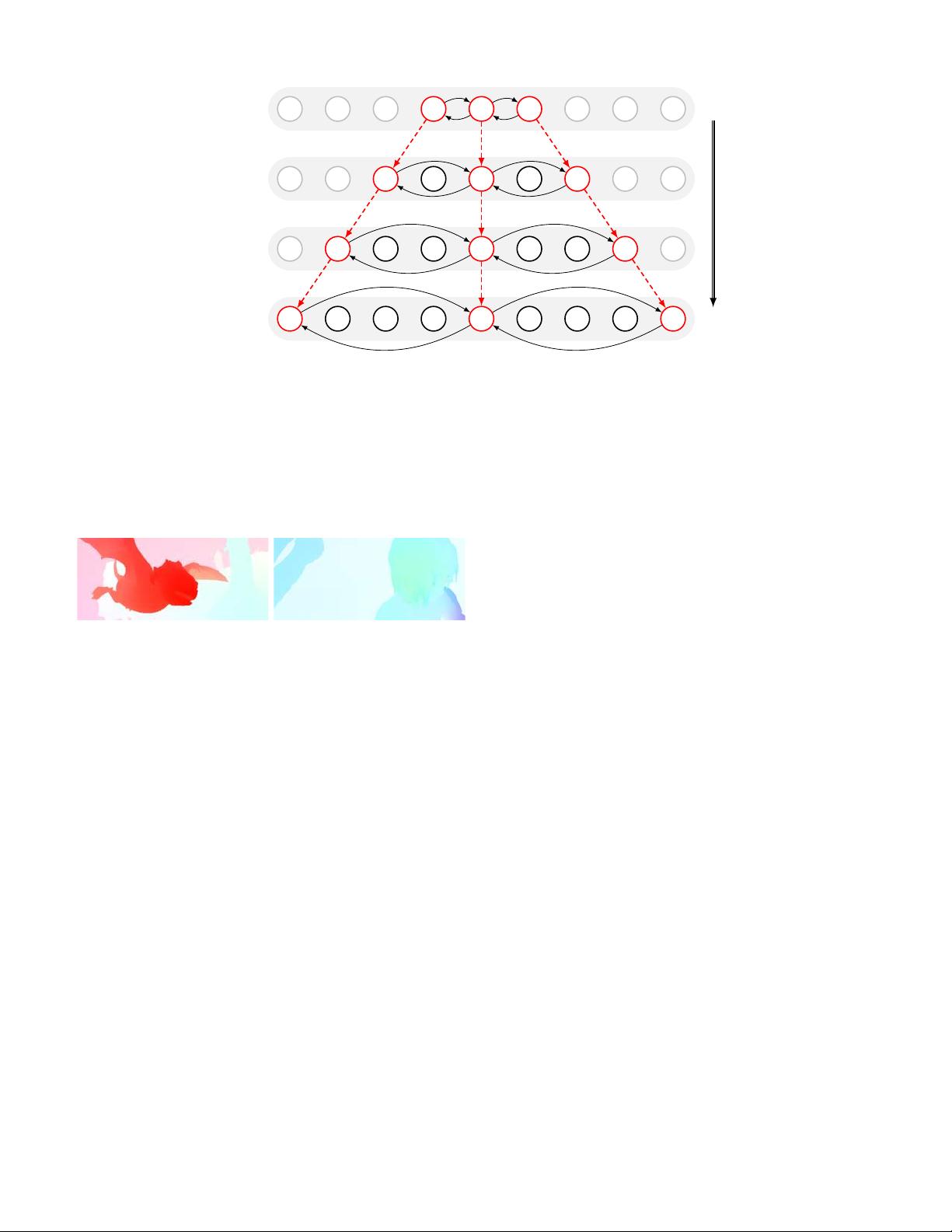
Fig. 3. Overview of the proposed CPM algorithm. After the construction of the pyramid, we choose seed points on each level (simple grid). The red circles

represent the seeds, and the neighbor propagation is performed between adjacent seeds (black arrows) to propagate good matches to adjacent seeds. For the

coarse-to-ﬁne scheme, the seeds on lower levels are initialized by higher-level seeds (red arrows).

Fig. 4. Example of PatchMatch on grid structure. Each column shows, from

top to bottom, the mean of two consecutive images, the ground truth and

the matching results of CPM with d = 11. Note that even with a large grid

spacing, the result captures most of the motion details.

(top-down) scheme. An overview of CPM matching is given in

Figure 3. We ﬁrst discuss PatchMatch in Section III-A and then

detail the matching procedure for one level of the pyramid in

Section III-B. Finally, we describe the hierarchical structures

of our approach, as well as the propagation between the levels,

in Section III-C.

A. PatchMatch

The objective of NNF algorithms is to ﬁnd the most

similar patch of all the patches in one image against another

under some patch distance metric. Connelly et al. proposed

a randomized algorithm, called PatchMatch [5], to efﬁciently

compute the approximate NNF.

PatchMatch has three main components. First, every pixel in

the image is initialized with either random matching offsets or

some prior information. Next, an iterative reﬁnement process is

applied over every pixel in an interleaved zig-zag and reverse

zig-zag manner, in which good matches are propagated to

adjacent pixels, followed by random search near the current

best matching offset.

neighborhood propagation and random search are the core

ideas of PatchMatch. Propagation is performed under the

assumption that the patch offsets are likely to be the same. For

example, if there is a good match near a pixel, the matching

of this pixel will be updated by the matching of the neighbor

if the patch distance (according to some patch distance metric)

of the neighbor is smaller. After propagation, a sequence of

randomly selected candidate offsets will be tested to improve

the current matching. The propagation and random search are

performed iteratively until convergence occurs or some ﬁxed

iteration numbers are achieved. We refer readers to [5] for

more detailed information.

PatchMatch has shown clear advantages in scene corre-

spondence [8] and structural image editing [5]. However, the

computed NNF is often very noisy because of the lack of

global regularization. We introduce a coarse-to-ﬁne structure

within the PatchMatch framework, which can reduce the noise

signiﬁcantly (see Figure 1(d)).

B. PatchMatch on Grid Structure

Considering the nature of the smoothness of optical ﬂow

compared with that of the NNF, we deﬁne our goal of matching

as ﬁnding the best match of some seeds rather than every

pixel of the image for efﬁciency. Formally, given two images

, I

⊂ R

and a collection of seeds S = {s

} at position

{p(s

)}, our goal is to determine the ﬂow of each seed

f(s

) = M(p(s

)) − p(s

) ∈ R

, where M(p(s

)) is

the corresponding matching position in I

for seed s

in I

In our method, the seeds are the cross points of the regular

image grid with a spacing of d pixels. Then, there is only one

seed in every d × d non-overlapping block (see Figure 4). We

will show that this fast approximation results in a signiﬁcant

speed-up with controllable accuracy.

Adopting the regular image grid, we obtain a default neigh-

bor system according to the spatial adjacency of the seeds on

the image grid. As in PatchMatch, neighborhood propagation

剩余11页未读，继续阅读

weixin_38638647

粉丝: 7
资源: 993

CPM：光流与立体声匹配的精细从粗到细 PatchMatch 方法

基于多尺度特征的遥感图像密集匹配方法

封装好的Harris算子提取特征点、匹配、提粗匹配类，添加到个人工程即可调用使用（基于opencv2）.-

Harris算子提取特征点、匹配、提粗匹配程序，（基于opencv）.-

卫星红外图像和视觉图像的粗到精细配准方法

行业分类-设备装置-工程图纸图框精细匹配方法及系统.zip

MPmain.rar_MPmain_匹配追踪_匹配追踪 时频_匹配追踪 频_时频原子分解

图像匹配算法研究图像匹配算法研究.pdf

让传感器匹配转换器还是让转换器匹配传感器

服务匹配机

SSJTextViewWithCanShrink匹配删除

最新资源

MPmain.rar_MPmain_匹配追踪_匹配追踪时频_匹配追踪频_时频原子分解