MATLAB中反向运动学与动力学干扰因素分析

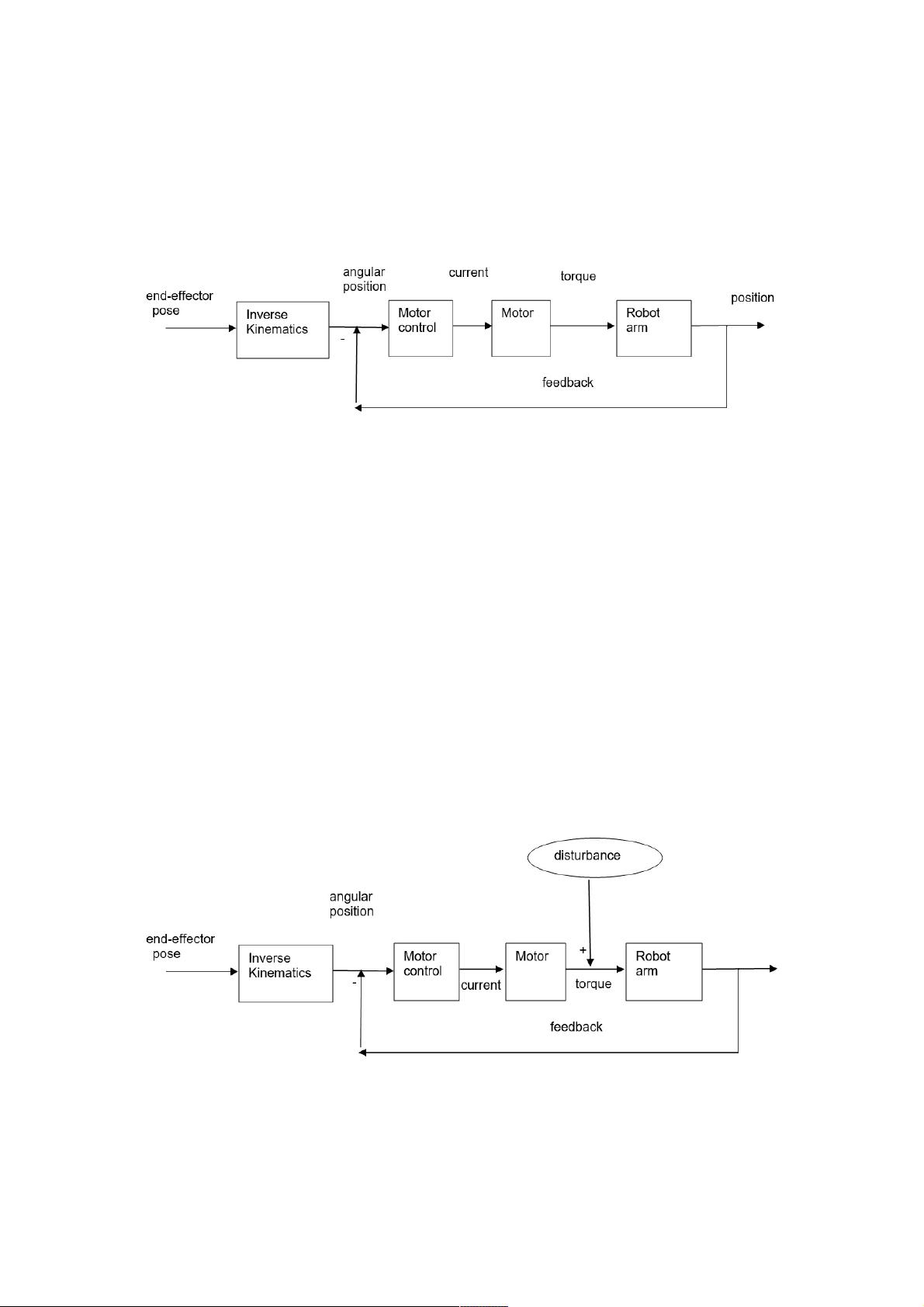
MATLAB中的机械臂算法——动力学 在MATLAB这一强大的数值计算环境中，机械臂的动力学分析是实现精确控制的关键部分。机械臂的动力学主要包括正向运动学和反向运动学两个方面。 正向运动学研究的是当知道所有关节的角度时，如何计算末端执行器（end-effector）的位置和姿态。这在设计路径规划或模拟机械臂运动时非常有用。然而，对于实际操作中的控制，反向运动学更为关键。它指的是已知末端执行器的位置和方向时，如何逆向计算出每个关节应有的角度。这在控制环路中至关重要，因为控制器需要根据目标位置来调整关节角度，从而驱动机械臂执行任务。 在反向运动学控制逻辑中，一旦得到末端执行器的pose，控制器首先计算出所需关节角度，并通过电机产生相应的力矩（torque）。同时，为了减小控制误差并应对干扰因素，系统采用反馈机制，通过实时监测执行器的实际状态与期望状态的差异，进行实时调整。 干扰因素是实际机械臂控制中不可避免的问题，包括地球引力、惯性、摩擦力、科里奥利力和离心力等。连杆间的耦合导致了反作用力和反向惯量的存在。此外，人为设定的需求如速度控制、碰撞保护等也被视为干扰。为了使机械臂“完美”运行，需要在控制环路中加入前馈控制，也就是提前计算和补偿这些干扰，用数学模型如： \[ u = M(q)qdd + C(q,qd)qd + G(q) \] 这里的\( u \)代表所需力矩，\( M(q) \)代表加速度惯量及连杆间惯量的矩阵，\( C(q,qd) \)处理科里奥利力和离心力的影响，\( G(q) \)则表示地球引力。这个方程是反向动力学的核心，它从关节角度\( q \)、速度\( qd \)和加速度\( qdd \)出发，预测每个关节所需的力矩，以实现预定的运动轨迹和性能。 正向动力学与反向动力学互为补充，前者用于理解机械臂的运动行为，后者则用于指导控制策略。在MATLAB中，通过编程和数值计算，工程师可以精确地设计和优化机械臂的运动控制，使其在复杂环境中稳定、高效地执行任务。通过深入理解和应用这些动力学原理，可以显著提升机械臂在工业自动化、机器人技术等领域中的性能和可靠性。