"最短路径问题:BFS算法详解及应用"
需积分: 0 111 浏览量
更新于2024-01-11
收藏 2.44MB PDF 举报
最短路径问题是图论中的经典问题之一,通过找到图中两个顶点之间的最短路径,可以帮助我们在很多实际应用中做出最优决策。在这个问题中,我们需要确定从一个给定的源点到其他每个顶点的最短路径。
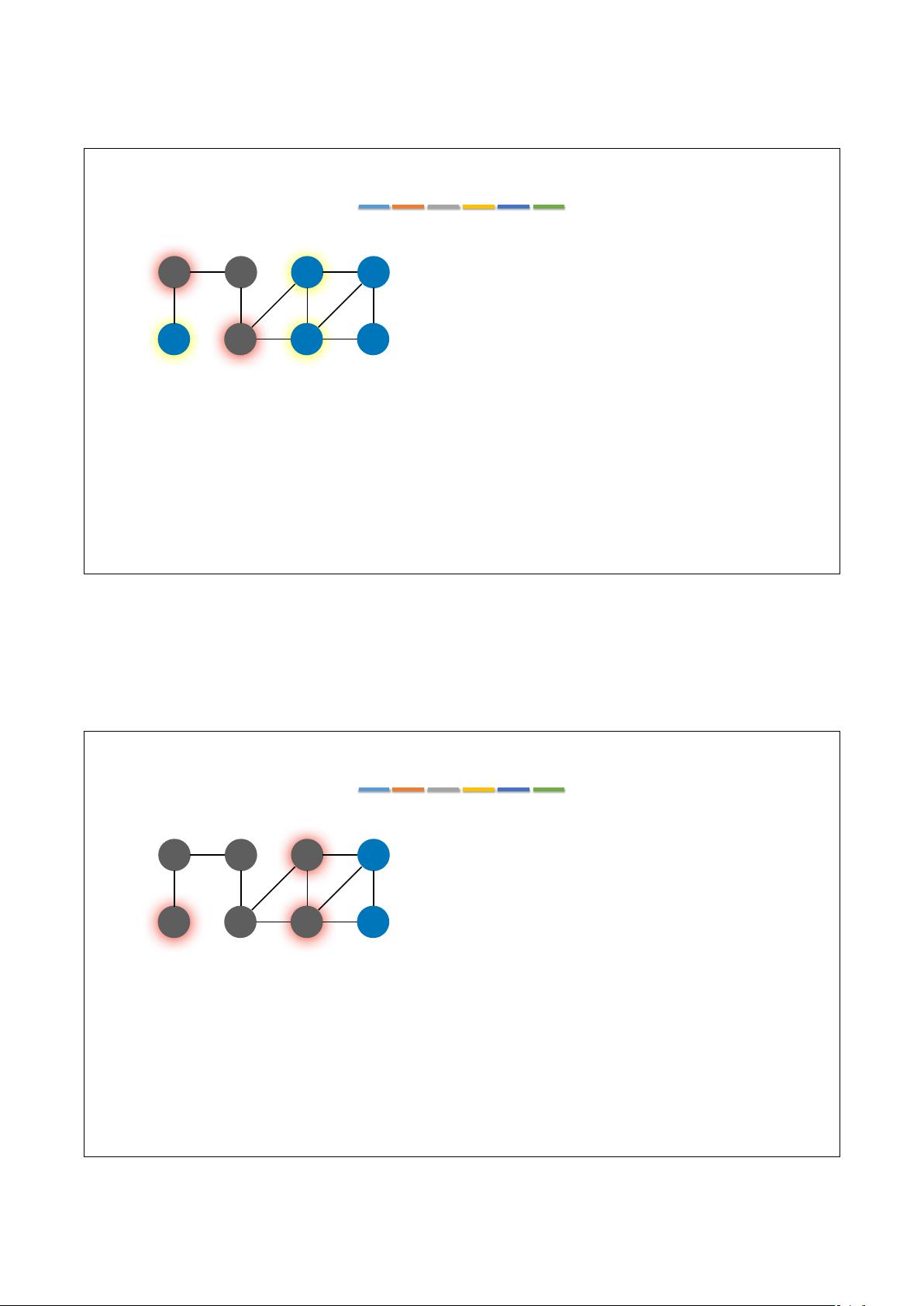
BFS(广度优先搜索)算法是解决最短路径问题的一种常用方法。该算法从源节点开始,先访问所有与源节点直接相邻的顶点,再逐层访问其他与当前已访问节点相邻的节点,直到找到目标节点或者所有节点均被访问完成。在BFS算法中,使用一个队列来存储待访问的节点,通过出队、入队的操作进行节点的遍历。
对于带权图的单源最短路径问题,我们可以将其视为一种特殊的带权图,其中所有边的权重都为1。在这种情况下,我们可以直接使用BFS算法来解决。具体步骤如下:
1. 创建一个队列,将源节点入队,同时初始化源节点到其他节点的距离为无穷大。
2. 将源节点的距离设为0。
3. 从队列中取出一个节点,并遍历其相邻节点。
4. 如果相邻节点的距离尚未被更新(即为无穷大),将其距离设置为当前节点的距离加1,并将其入队。
5. 重复步骤3和4,直到队列为空。
6. 最后,我们可以得到源节点到其他每个节点的最短路径。
在具体应用中,比如物流集散中心需要将货物运送到各个城市,我们可以使用BFS算法来确定距离最近的城市,从而优化物流运输成本。此外,不同城市之间也需要相互往来,我们可以利用每对顶点间的最短路径,找到相互之间的最短距离,从而提高交通效率。
对于无权图的单源最短路径问题,我们同样可以使用BFS算法来解决。由于无权图中所有边的权重都相同,即为1,因此BFS算法依然适用于该问题。我们只需要将带权图中的所有边的权值设为1即可。
综上所述,最短路径问题是图论中的重要问题之一,通过使用BFS算法,我们可以高效地找到图中两个顶点之间的最短路径。无论是带权图还是无权图,BFS算法都可以有效应用于解决单源最短路径问题,帮助我们在实际应用中做出最优决策。
2022-08-03 上传
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情