非线性方程数值解法：从二分法到迭代解

"非线性方程的数值解" 在数学和工程领域，非线性方程的求解是一项重要的任务，因为它们广泛存在于各种实际问题中。非线性方程是指那些不能表示为变量的线性组合的方程，即函数f(x)不是线性的。非线性方程的一般形式为f(x) = 0，其中f(x)是一个关于变量x的非线性函数。 非线性方程的根，即满足f(x) = 0的x值，也被称为函数f(x)的零点。如果f(x)可以分解为f(x) = (x - x*)^m * g(x)，其中m是正整数，x*是f(x)的m重零点。当m=1时，x*被称为单根。对于m重根，有一个重要的判据：如果f(x)存在m阶导数，并且在x*处满足f^(m)(x*) ≠ 0，那么x*是f(x)的m重根。 在处理非线性方程时，我们通常会遇到两类方程：代数方程和超越方程。代数方程是多项式函数构成的方程，而超越方程则包括三角函数、指数函数、对数函数等。一次和二次代数方程可以通过解析方法求解，但三次及以上次数的代数方程和超越方程往往没有封闭形式的解，因此需要采用数值方法求解。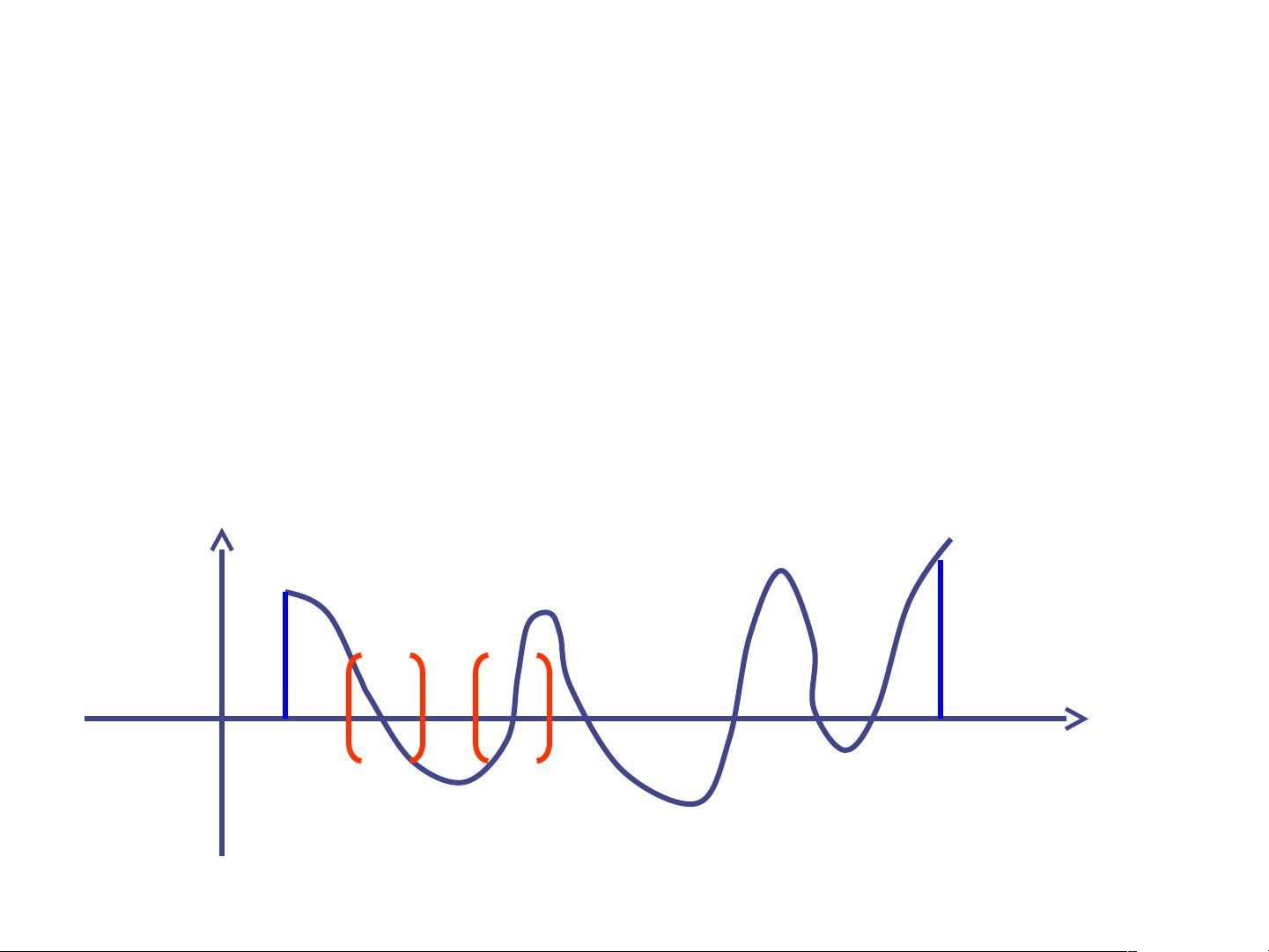 数值解法通常包括三个步骤：首先，我们需要确定方程是否有根以及根的数量；其次，我们要找到根所在的区间，这通常是通过寻找函数值符号改变的区间来实现的；最后，使用迭代方法逐步精确化根的近似值，直至达到预设的精度要求。 二分法是一种简单的数值解法，适用于在已知函数f(x)在闭区间[a, b]上连续，并且f(a) * f(b) < 0的情况。这意味着f(x)在(a, b)内必然有一个零点。二分法的基本思想是不断将包含零点的区间对半分割，然后检查每个子区间的端点函数值的符号，以确定零点所在的新区间。这个过程重复进行，直到达到所需的精度。 在应用二分法时，关键在于选择合适的初始区间和确定何时停止迭代。为了确保算法的收敛，需要设定一个最小的区间长度或者一个最大迭代次数。此外，还需要处理可能存在的多重根或函数在某点不可微的情况，这可能会影响二分法的效率和准确性。 除了二分法，还有其他数值解法，如牛顿-拉弗森法、 secant 法、Halley法等，它们利用函数及其导数的信息来构造迭代公式，通常比二分法收敛更快，但可能需要更多的计算量。这些方法在处理非线性方程时提供了多样化的选择，可以根据具体问题的特性和计算资源来选择合适的方法。