稀疏表示提升面部识别鲁棒性：对抗变化与遮挡

5星 · 超过95%的资源需积分: 11 22 浏览量更新于2024-08-01 收藏 3.02MB PDF 举报

在最新的研究中，"Robust Face Recognition via Sparse Representation"（鲁棒人脸识别通过稀疏表示）由John Wright、Allen Y. Yang、Arvind Ganesh、S. Shankar Sastry和Yi Ma等专家提出，他们针对人脸识别领域提出了一个革命性的方法。该论文关注的是如何在复杂的环境下自动识别人脸，包括面部表情变化、光照条件变化、遮挡以及伪装等问题。他们将人脸识别问题重新定义为多线性回归模型分类，并强调了稀疏信号表示理论在解决这一问题中的关键作用。论文的核心观点是利用L1最小化技术来计算稀疏表示，从而设计出一种通用的图像对象识别算法。这种新框架对人脸识别中的两个关键问题提供了新的见解：特征提取和遮挡鲁棒性。作者指出，与传统方法不同，如果能够有效利用稀疏性，特征选择的重要性就会减弱。真正关键的是特征数量是否足够大，以及稀疏表示是否被准确地计算出来。在特征提取方面，稀疏表示的优势在于，即使在特征选择不那么严格的情况下，通过寻找数据中最少的非零元素，依然能捕捉到关键信息。这使得系统能够更好地适应各种输入，提高识别的稳定性和准确性。同时，对于遮挡问题，稀疏表示能够提供一种内在的抗干扰能力，因为较少的非零元素意味着对缺失或部分信息的容忍度更高。此外，论文可能还探讨了如何优化稀疏编码过程，例如使用高效的算法如ISTA（Iterative Shrinkage-Thresholding Algorithm）或FISTA（Fast Iterative Shrinkage-Thresholding Algorithm），以确保在实际应用中达到高效且精确的识别效果。通过实验验证，这种基于稀疏表示的算法在训练样本相对较少的情况下也能展现出优秀的识别性能，证明了其在实际人脸识别系统的潜力和价值。 "Robust Face Recognition via Sparse Representation"不仅提升了人脸识别的准确度，还革新了我们对特征提取和鲁棒性处理的理解，为处理复杂环境下的人脸识别任务开辟了新的研究方向。在未来的研究和实际应用中，这种稀疏表示的方法有望进一步推动人脸检测、识别技术的发展，尤其是在资源有限或者实时性要求高的场景下。

As the entries of the vector xx

encode the identity of the

test sample yy, it is tempting to attempt to obtain it by

solving the linear system of equations yy ¼ Axx. Notice,

though, that using the entire training set to solve for xx

represents a significant departure from one sample or one

class at a time methods such as NN and NS. We will later

argue that one can obtain a more discriminative classifier

from such a global representation. We will demonstrate its

superiority over these local methods (NN or NS) both for

identifying objects represented in the training set and for

rejecting outlying samples that do not arise from any of the

classes present in the training set. These advantages can

come without an increase in the order of growth of the

computation: As we will see, the complexity remains linear

in the size of training set.

Obviously, if m>n, the system of equations yy ¼ Axx is

overdetermined, and the correct xx

can usually be found as

its unique solution. We will see in Section 3, however, that

in robust face recognition, the system yy ¼ Axx is typically

underdetermined, and so, its solu tion is not unique.

Conventionally, this difficulty is resolved by choosing the

minimum ‘

-norm solution:

ð‘

Þ :

¼ arg min kxxk

subject to Axx ¼ yy: ð4Þ

While this optimization problem can be easily solved (via

the pseudoinverse of A), the solution

is not especially

informative for recognizing the test sample yy. As shown in

Example 1, ^xx

is generally dense, with large nonzero entries

corresponding to training samples from many different

classes. To resolve this difficulty, we instead exploit the

following simple observation: A valid test sample yy can be

sufficiently represented using only the training samples

from the same class. This representation is naturally sparse if

the number of object classes k is reasonably large. For

instance, if k ¼ 20, only 5 percent of the entries of the

desired xx

should be nonzero. The more sparse the

recovered xx

is, the easier will it be to accurately determine

the identity of the test sample yy.

This motivates us to seek the sparsest solution to yy ¼ Axx,

solving the following optimization problem:

ð‘

Þ :

¼ arg min kxxk

subject to Axx ¼ yy; ð5Þ

where kk

denotes the ‘

-norm, which counts the number

of nonzero entries in a vector. In fact, if the columns of A are

in general position, then whenever yy ¼ Axx for some xx with

less than m=2 nonzeros, xx is the unique sparsest solution:

¼ xx [33]. However, the problem of finding the sparsest

solution of an underdetermined system of linear equations is

NP-hard and difficult even to approximate [13]: that is, in the

general case, no known procedure for finding the sparsest

solution is significantly more efficient than exhausting all

subsets of the entries for xx.

2.2 Sparse Solution via ‘

-Minimization

Recent development in the emerging theory of sparse

representation and compressed sensing [9], [10], [11] reveals

that if the solution xx

sought is sparse enough, the solution of

the ‘

-minimization problem (5) is equal to the solution to

the following ‘

-minimization problem:

ð‘

Þ :

¼ arg min kxxk

subject to Axx ¼ yy: ð6Þ

This problem can be solved in polynomial time by standard

linear programming methods [34]. Even more efficient

methods are available when the solution is known to be

very sparse. For example, homotopy algorithms recover

solutions with t nonzeros in Oðt

þ nÞ time, linear in the size

of the training set [35].

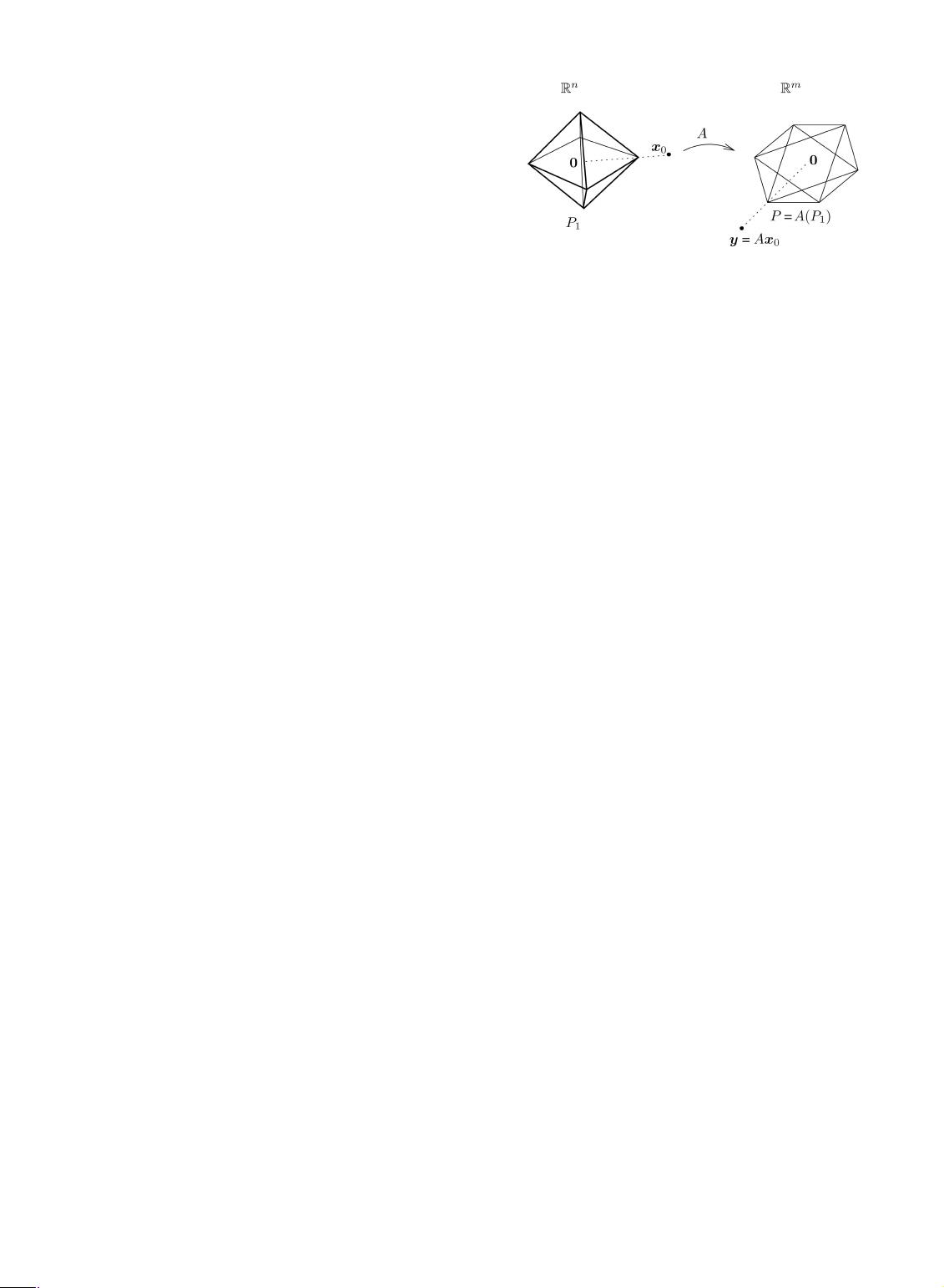
2.2.1 Geometric Interpretation

Fig. 2 gives a geometric interpretation (essentially due to

[36]) of why minimizing the ‘

-norm correctly recovers

sufficiently sparse solutions. Let P



denote the ‘

-ball (or

crosspolytope) of radius :



fxx : kxxk

 gIR

: ð7Þ

In Fig. 2, the unit ‘

-ball P

is mapped to the polytope

P¼

AðP

ÞIR

, consisting of all yy that satisfy yy ¼ Axx for

some xx whose ‘

-norm is  1.

The geometric relationship between P



and the polytope

AðP



Þ is invariant to scaling. That is, if we scale P



, its

image under multiplication by A is also scaled by the same

amount. Geometrically, finding the minimum ‘

-norm

solution

to (6) is equivalent to expanding the ‘

-ball P



until the polytope AðP



Þ first touches yy. The value of  at

which this occurs is exactly k

Now, suppose that yy ¼ Axx

for some sparse xx

. We wish

to know when solving (6) correctly recovers xx

.This

question is easily resolved from the geometry of that in

Fig. 2: Since

is found by expanding both P



and AðP



until a point of AðP



Þ touches yy, the ‘

-minimizer

must

generate a point A

on the boundary of P .

Thus,

¼ xx

if and only if the point Aðxx

=kxx

Þ lies on

the boundary of the polytope P. For the example shown in

Fig. 2, it is easy to see that the ‘

-minimization recovers all

with only one nonzero entry. This equivalence holds

because all of the vertices of P

map to points on the

boundary of P.

In general, if A maps all t-dimensional facets of P

facets of P , the polytope P is referred to as (centrally)

t-neighborly [36]. From the above, we see that the

‘

-minimization (6) correctly recovers all xx

with  t þ 1

nonzeros if and only if P is t-neighborly, in which case, it is

WRIGHT ET AL.: ROBUST FACE RECOGNITION VIA SPARSE REPRESENTATION 213

Fig. 2. Geometry of sparse representation via ‘

-minimization. The

‘

-minimization determines which facet (of the lowest dimension) of the

polytope AðP



Þ, the point yy=kyyk

lies in. The test sample vector yy is

represented as a linear combination of just the vertices of that facet, with

coefficients xx

6. Furthermore, even in the overdetermined case, such a linear equation

maynotbeperfectlysatisfiedinthepresenceofdatanoise(see

Section 2.2.2).

7. This intuition holds only when the size of the database is fixed. For

example, if we are allowed to append additional irrelevant columns to A,

we can make the solution xx

have a smaller fraction of nonzeros, but this

does not make xx

more informative for recognition.

剩余17页未读，继续阅读

wdmjx

粉丝: 1
资源: 3

稀疏表示提升面部识别鲁棒性：对抗变化与遮挡

Robust face recognition via sparse representation

PAMI-Robust FaceRecognition via Sparse Representation

Low-rank constrained collaborative representation for robust face recognition

robust face recognition algorithm

Iterative Re-constrained Group Sparse Face Recognition

Sparse Alignment for Robust Tensor Learning

stacked convolutional sparse denoising autoencoder

CPPC++_低成本实现Wooting键盘的Rapid trigger功能不必为几个按键购买整个键盘人人都能做Wouo.zip

CPPC++_可能是世界上最快的协同程序库.zip

ConsulHelper，.Net微服务基础框架，已支持.NetCore，具备服务发现、健康检查、服务分级、分布式配置.zip

最新资源