ICESat-2 ATL06: Land Ice Height Processing Algorithm Theoretical Basis

版权申诉

138 浏览量更新于2024-07-07 1 收藏 4.6MB PDF 举报

"ICESAT-2_ATL06_ATBD_r004.pdf" 是一个关于ICESat-2（冰、云和陆地高度卫星-2）任务的算法理论基础文档，专注于陆地冰沿轨道高度产品（ATL06）。此文档由NASA的戈达德太空飞行中心的专家团队编写，详细阐述了陆地冰高程处理算法的理论基础，以及由此任务生成的产品。 ICESat-2是美国国家航空航天局（NASA）的一个项目，旨在通过其先进的地形激光测高仪系统（ATLAS）精确测量全球冰层、云层和陆地的海拔变化。ATLAS不仅包含了科学算法软件（ASAS）和调度与数据管理系统（SDMS），还支持在ICESat-2空间飞船上进行的数据处理。ASAS能够生成从0级到4级的标准数据产品，同时提供产品质量评估和元数据信息。这篇文档的核心内容是陆地冰高程产品（ATL06）的算法理论。它涵盖了产品提供的各个参数的描述，以及在衍生这些产品时使用的辅助地球物理参数。文档的目的是为了使科学家和研究人员理解ICESat-2如何处理和解析来自ATLAS的数据，以得出准确的冰层高度信息。高度产品ATL06提供了沿卫星轨道的陆地冰层的详细高程数据，这些数据对于监测冰川消融、极地冰盖的变化以及全球海平面上升的研究至关重要。文档的摘要部分强调，这份资料详细解释了陆地冰高程处理算法的原理，以及每个产品附带的参数和辅助参数的使用，这些参数用于计算最终的高程结果。此外，该文档可能还涵盖了数据质量控制方法、误差分析、数据处理流程，以及如何将ATLAS的脉冲激光测距数据转换为高精度的地表高度信息。对于从事冰川学、气候学、地球物理学等领域研究的科学家，这个文档是理解ICESat-2数据的关键参考资料，也是进行数据分析和建模的重要工具。 ICESat-2_ATL06_ATBD_r004.pdf是ICESat-2项目中陆地冰高程测量技术的详尽指南，它揭示了复杂的卫星数据处理背后的科学原理，为冰层研究提供了坚实的基础。

ICESat-2 Algorithm Theoretical Basis Document for Land Ice Height (ATL06)

Release 004

2.2 Physical Basis of Measurements

2.2.1 Height retrieval over approximately planar surfaces

Light from the ATLAS lasers reaches the earth’s surface as flat disks of down-traveling photons,

approximately 50 cm in vertical extent, and spread over about 17 m horizontally. On land ice,

photons are scattered once, or many times, by snow and ice grains, into every direction,

including towards the satellite; a tiny fraction return to the ATLAS telescope’s focal plane, and a

few of these are counted by the detector electronics and recorded as Photon Events (PEs). Over

the vast majority of the earth’s land ice, the surface is smooth, with small (single-degree)

variations in surface slopes at scales less than a few hundred meters. This allows us to

approximate the surface profiles measured by ATLAS with short linear segments. We aggregate

PEs received by ATLAS into 50% overlapping along-track segments of a fixed length (40 m),

whose centers are 20 m apart. We then fit these PEs with sloping line segments; for each

segment, we estimate both the along-track slope and the height at the center of the segment.

When both beams in a pair provide height measurements, we also calculate the across-track

slope for the pair. Any height variation not captured by this fitting process will be treated as

surface roughness.

The time variation in surface height is determined by fitting a simple spatial function to the

heights from multiple repeat measurements, and using this function to correct the measurements

100

for the height variations caused by spatial sampling of sloped and curving surfaces. This

101

function is fit to the subset of the repeat measurements that we assess to be of the highest quality,

102

but corrected height estimates are provided for all available repeats, and data-quality metrics are

103

provided to allow users to decide which heights to use.

104

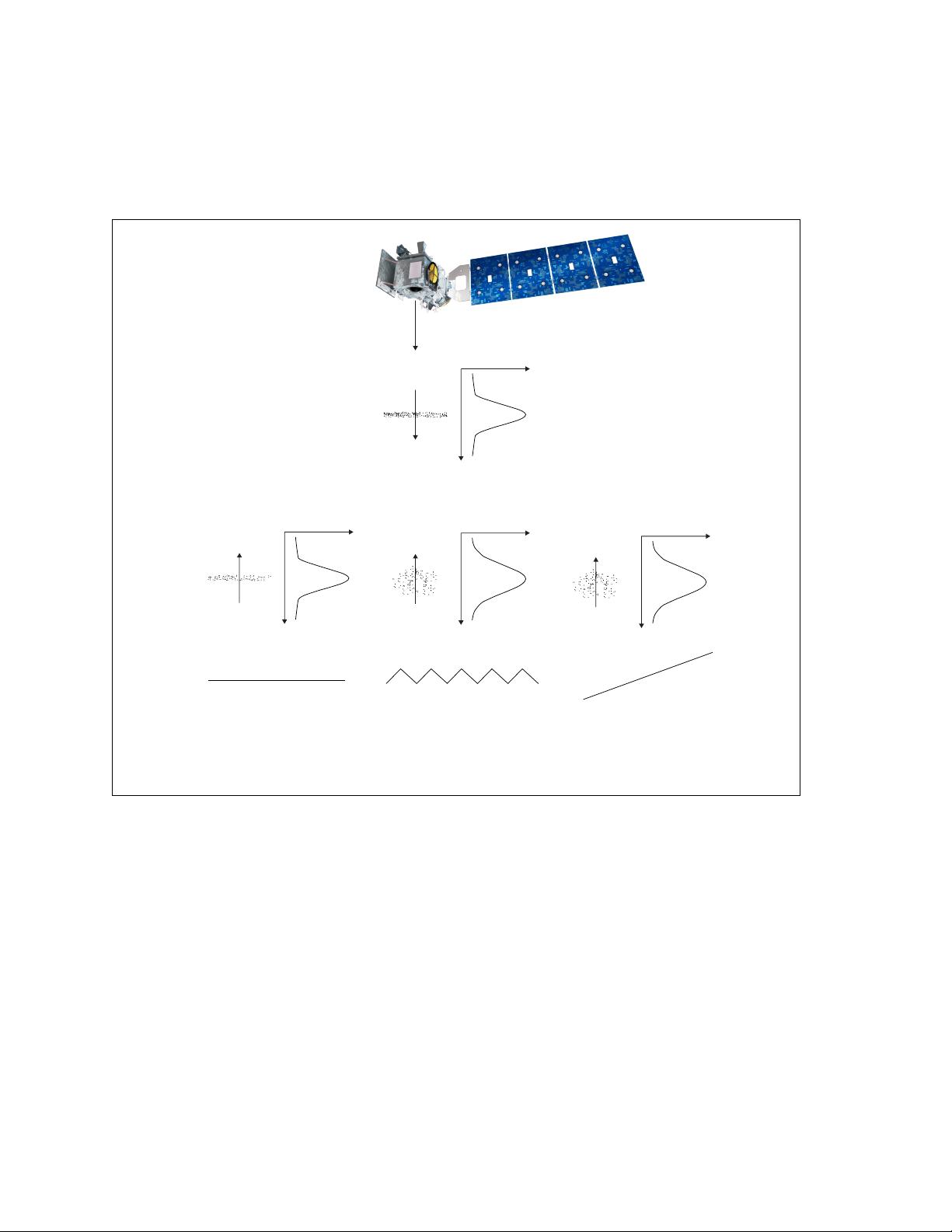
2.2.2 Effects of surface slope and roughness

105

Figure 2-2 shows how slope and roughness contribute to the shape of the return pulse. For many

106

areas of glaciers, the ground may be treated as a rough planar surface, and the laser pulse as

107

having a Gaussian distribution in space, with intensity falling to 1/e

of its peak value over a

108

distance W/2. The laser pulses also have an approximate Gaussian distribution in time, with

109

standard deviation

. If the incident beam is not parallel to the surface normal, photons from the

110

edge of the footprint farthest from the satellite will be delayed relative to photons from the edge

111

nearest the satellite. At the same time, a rough surface will yield early photons and late photons,

112

further spreading the returned photons. If the angle between the beam and the surface normal is

113

j, and the surface height within the footprint has a Gaussian distribution with RMS deviation R

114

relative to the plane of the surface, then the measured temporal distribution of the returned

115

photons will be Gaussian as well (Yi & Bentley, 1999), with a temporal standard deviation equal

116

to the quadratic sum of the spreads due to the transmitted pulse, the surface slope, and the

117

roughness:

118

!"#$

&'()

(/$

For ATLAS,

*+,-

is expected to be around 4.25 m (one quarter of W), and s

around 0.68 ns,

119

corresponding to a FWHM (Full Width at Half Maximum) of 1.6 ns, so spreading due to sloping

120

ICESat-2 Algorithm Theoretical Basis Document for Land Ice Height (ATL06)

Release 004

Sunlight scattered from bright (i.e. snow-covered) surfaces will produce detected PEs at rates up

136

to around 12 MHz. For comparison, a return with as few as three PEs distributed over one half

137

meter of range produces a brief return rate of 900 MHz. Signal returns are also distinct from the

138

background because they are spatially contiguous, so that PEs will be clustered in time in a

139

consistent way from one shot to the next.

140

2.3 Potential Errors

141

Errors in ATLAS land-ice products can come from a variety of sources:

142

1) Sampling error: ATLAS height estimates are based on a random sampling of the surface

143

height distribution;

144

2) Background noise: Random-noise PEs are mixed with the signal PEs, so sampled PEs

145

will include random outliers;

146

3) Complex topography: The along-track linear fit and across-track polynomial fit do not

147

always resolve complex surface topography.

148

4) Misidentified PEs: The ATL03 product will not always identify the correct PEs as signal

149

PEs;

150

5) First-photon bias: This is an error inherent to photon-counting detectors that results in a

151

high bias in the mean detected PE height that depends on signal strength;

152

6) Atmospheric forward scattering: Photons traveling downward through a cloudy

153

atmosphere may be scattered through small angles but still be reflected by the surface

154

within the ATLAS field of view; these will be delayed, producing an apparently lower

155

surface;

156

7) Subsurface scattering: Photons may be scattered many times within ice or snow before

157

returning to the detector; these will be delayed, producing a surface estimate with a low

158

bias.

159

These errors are each treated in a different way during the ATL06 processing:

160

1) and 2) are treated as random errors, and their effects are quantified in the error estimates

161

associated with the products.

162

3) and 4) will produce relatively large errors, and will need to be addressed with consistency

163

checks on the data during the generation of higher-level products.

164

5) will be corrected routinely during ATL06 processing (see Section 3.0).

165

6) and 7) require information about cloud structure and ice-surface conditions that will not be

166

available at the time of processing of ATL06. Correcting for these errors remains an active

167

avenue for research.

168

2.4 Land-ice Level-3 products: ATL06: Land-Ice Height

169

The ATL06 product provides surface height estimates organized by reference -pair track (RPT),

170

in a format designed to facilitate comparison between different repeat measurements on the same

171

RPT. It also combines information from the two beams in each PT to give across-track slope

172

estimates. A variety of parameters are provided that indicate the quality of the surface-height

173

estimates and the signal and noise levels associated with the measurement. Note that in cycles 1

174

ICESat-2 Algorithm Theoretical Basis Document for Land Ice Height (ATL06)

Release 004

and 2 of the mission, ICESat-2 did not point at the RPTS, and ICESat2’s pairs are offset by up to

175

2 km from the RPT locations. The first cycle that was collected over the RPTS was the third.

176

We define ATL06 heights based on fits of a linear model to ATL03 height data from short

177

(40 m) segments of the ground track, centered on reference points spaced at 20-m intervals

178

along-track. We refer to height estimates for these short segments as “segment heights”, and

179

segment’s horizontal location is that of the reference point, displaced in a direction perpendicular

180

to the RGT to match the GT offset. The choice of 40 m for the segment length provides data

181

from slightly more than two independent (non-overlapping) ATL03 heights (based on 17-m

182

footprints) for the along-track slope estimate, so that this component of the slope can be

183

eliminated as a cause of vertical scatter in the PE height distribution. The spacing between

184

reference points is 20 m, so that each segment overlaps its neighbors by 50%. Defining

185

overlapping segments in this way increases the chances that a segment will overlap a locally

186

smooth area within a crevasse field, potentially improving elevation-rate recovery in these areas.

187

We use the same along-track sampling for both beams in each beam pair, and, for each cycle, use

188

the same reference point each time we calculate a segment height. This allows for direct

189

comparison between segment heights from the same RPT, without the need to interpolate in the

190

along-track direction. The ATL03 PE used for each segment can be determined by associating

191

the /gtxx/land_ice_segments/segment_id parameter in ATL06 with the

192

/gtxx/geolocation/segment_id parameter in ATL03: segment m in ATL06 includes PEs from

193

ATL03 segments m-1 and m (here xx represents the ATLAS beam, with gt1l and gt1r providing

194

the left and right beams for pair 1).

195

A minimal representation of the data is given in datasets in the ATL06 product in the

196

/gtxx/land_ice_segments groups. In these groups, we give the latitude, longitude, height, slope,

197

vertical error estimate, and a quality flag for each segment. This represents the minimum set of

198

parameters needed by most users; a wide variety of parameters describing the segment fit, the

199

input data, and the environmental conditions for the data are available in the subgroups within

200

the gtxx groups.

201

剩余103页未读，继续阅读

空中旋转篮球

粉丝: 5576
资源: 47

ICESat-2 ATL06: Land Ice Height Processing Algorithm Theoretical...

最新资源

ICESat-2 ATL06: Land Ice Height Processing Algorithm Theoretical...

ICESat-2 ATL03产品处理算法及理论基础

ICESat-2 ATL08 ATBD v004：陆地植被沿轨道产品算法概述

ICESat-2 ATL13: 内陆水体数据产品算法基础

ICESat2_ATL09_Layer_Parameters.pdf

icesat2-atl03-atbd-r005-0.pdf ATL03算法文档

ICESat2_ATL16_ATL17_ATBD_r002.pdf

ICESat2_ATL07_ATL10_ATBD_r004.pdf

ICESat2_ATL03g_ATBD_r002.pdf

ICESat2_ATL08_ATBD_r004.pdf

ICESat2_ATL13_ATBD_r003.pdf

最新资源