算法导论第三版答案：选择排序与二分查找解析

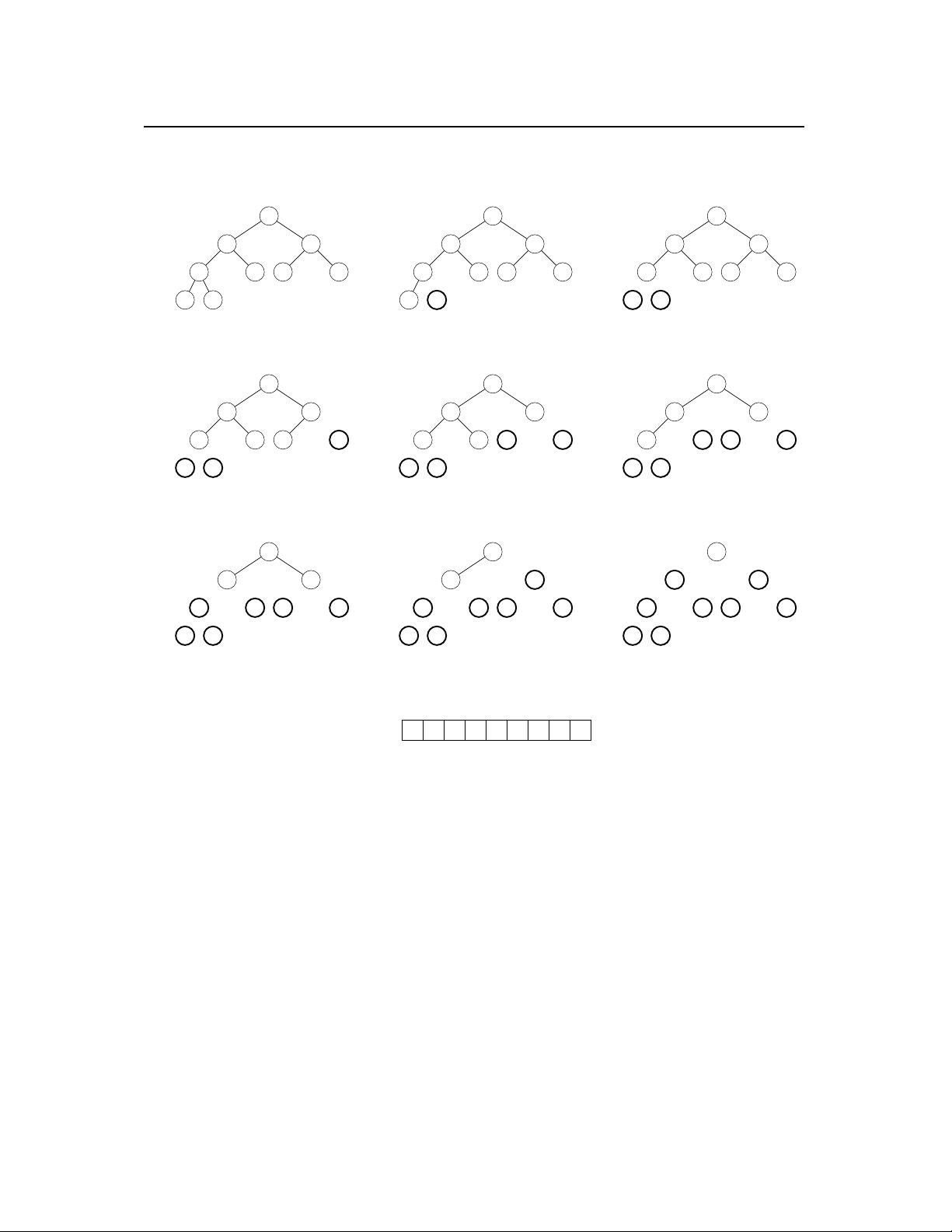
"算法导论课程的第三版答案，包含部分章节练习的解答，主要涉及算法的实现和分析。" 在《算法导论》这本经典的教材中，它提供了许多算法的设计、分析以及实现方法。这里提到的是第二章“Getting Started”部分的一些习题解答，主要包括了对Selection-Sort算法的解析。 Selection-Sort是一种简单的排序算法，其工作原理如下： 1. 在外层循环中，算法遍历数组的前n个元素（从下标1到n）。 2. 对于每个j，内层循环会找到当前子数组A[1:j-1]中的最小元素，并将其存储在变量smallest中。 3. 如果在内层循环中找到一个比smallest更小的元素A[i]，则更新smallest为i，并交换A[j]和smallest的值。 4. 这个算法保持了一个循环不变量：在外层循环开始时，子数组A[1:j-1]包含了A[1:n]中前j个最小的元素，并且这个子数组已经排序。 5. 当外层循环结束时，子数组A[1:n-1]包含了所有n-1个最小元素，并且排序完成，因此A[n]是最大的元素。 6. Selection-Sort的时间复杂度为O(n^2)，适用于所有情况。 此外，针对第2.2-4题的解答提到了算法的特殊情况处理。某些算法在特定输入情况下可能有更快的运行时间，但这通常不能代表其一般性能。对于算法的评估，应关注其在最坏、平均和最好情况下的表现，而不是仅仅依赖最好情况。 最后，第2.3-5题涉及到二分查找（Binary-Search）算法，这是一个在已排序数组中查找特定元素的有效方法： 1. 二分查找算法接受一个排序好的数组A、要查找的值v和数组范围low到high。 2. 它首先计算中间元素的位置，并与目标值v进行比较。 3. 如果中间元素等于v，则找到了目标；如果中间元素小于v，搜索范围移到中间元素的右侧；如果中间元素大于v，则搜索范围移到左侧。 4. 每次比较后，搜索范围都会减半，直到找到目标值或搜索范围为空。 二分查找的时间复杂度为O(log n)，在大规模数据中表现出高效的性能。然而，它依赖于输入数据已经排序，否则无法正确工作。 这些解答揭示了算法分析的基本概念，包括时间复杂度的评估、循环不变量的使用以及对特殊情况的处理，这些都是理解和设计高效算法的关键。