信号与系统第二章：线性时不变系统分析

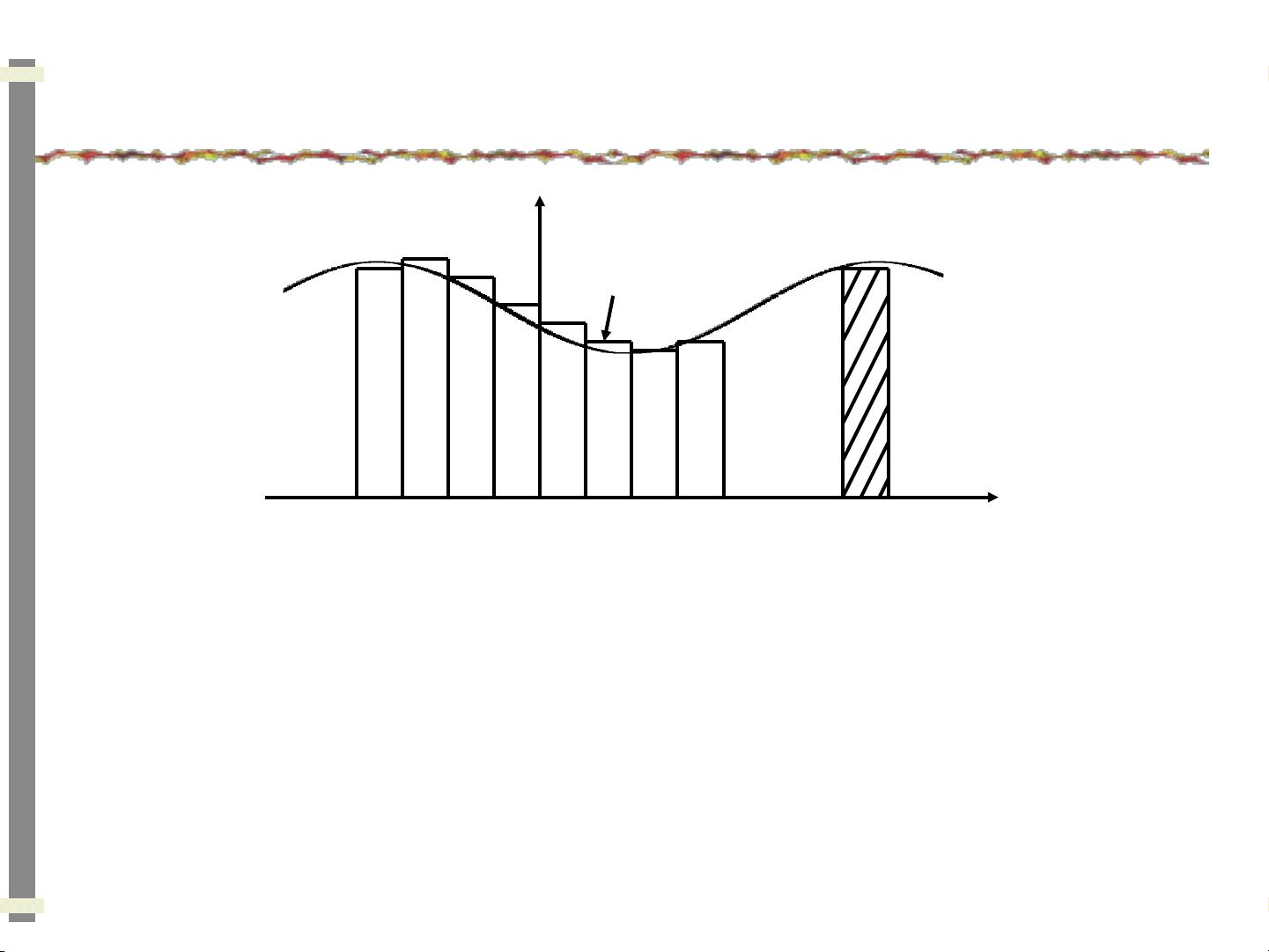
该资源是中山大学《信号与系统》课程的第二章课件，主要讲解线性时不变系统（LTI系统）的概念、分析方法和应用。课件内容涵盖了信号的时域分解、LTI系统的时域分析、系统性质、微分方程和差分方程表示、框图表示以及奇异函数等。 在信号与系统领域，LTI系统是一个核心概念，它满足齐次性和可加性，同时保持时间不变性。这一特性使得分析复杂信号通过系统后的响应变得相对简单。基本思路是将任意输入信号分解为基本信号的线性组合，然后利用LTI系统的线性特性，将系统对任意输入信号的响应表达为系统对这些基本信号响应的线性组合。 第二章主要分为以下几个部分： 1. 信号的时域分解：离散时间信号用δ(n)表示，连续时间信号用δ(t)表示。任何信号都可以分解为这些基本信号的线性组合。例如，离散时间信号x(n)可以表示为不同加权和位置的单位脉冲δ(n-k)的和。 2. LTI系统的时域分析：重点介绍了卷积和与卷积积分的概念。对于离散时间LTI系统，卷积和是计算系统响应的关键工具。卷积和定义为：对于任何离散时间信号x(n)，其通过LTI系统后的输出y(n)可以通过将x(n)和系统单位脉冲响应h(n)做卷积得到，即y(n) = ∑[x(k) * h(n-k)]。 3. LTI系统的性质：包括系统对线性组合输入的线性响应、延迟输入的时间平移不变性、尺度输入的尺度不变性等。 4. LTI系统的微分方程及差分方程表示：LTI系统可以用微分方程（连续时间）或差分方程（离散时间）来描述其内部动态行为。 5. LTI系统的框图结构表示：通过框图可以直观地理解系统功能，便于系统设计和分析。 6. 奇异函数：在信号处理中，某些特殊函数如单位阶跃函数、单位脉冲函数等，因其独特的性质，在分析LTI系统时有重要应用。 通过深入学习这部分内容，学生将掌握LTI系统的分析基础，为后续的频域分析和变换域分析打下坚实的基础。同时，了解和掌握卷积和的计算方法对于解决实际问题至关重要，因为卷积是求解系统响应的基本工具，广泛应用于通信、滤波器设计、图像处理等多个领域。