动态规划：算法设计关键

动态规划是算法设计与分析课程中的关键概念，它是由美国数学家Richard Bellman在20世纪50年代发展起来的一种高效解决多阶段决策过程中的最优问题的方法。在“算法设计与分析课件-第八章 动态规划”中，主要内容涵盖了以下几个要点： 1. 动态规划的定义：动态规划是一种算法设计技术，主要用于解决那些具有最优子结构和无后向性的最优化问题。"编程"在这里指的是策略规划和规划的过程，意味着通过解决子问题来构建整个问题的最优解。 2. 适用条件： - 最优化原理：问题的子问题最优解组合即为原问题的最优解，这使得我们能够通过自底向上的方法找到整体最优解。 - 无后向性：每个阶段的决策只依赖当前状态，不考虑过去的决策，确保问题的状态具有独立性。 - 子问题重叠性：虽然不是必须条件，但重复计算相同子问题可以提高效率，动态规划以空间换取时间。 3. 基本思路：动态规划的实施包括识别最优解结构、定义递归关系、自底向上求解最优值以及根据这些信息构造最优解。与分治法相比，动态规划关注子问题间的交互性。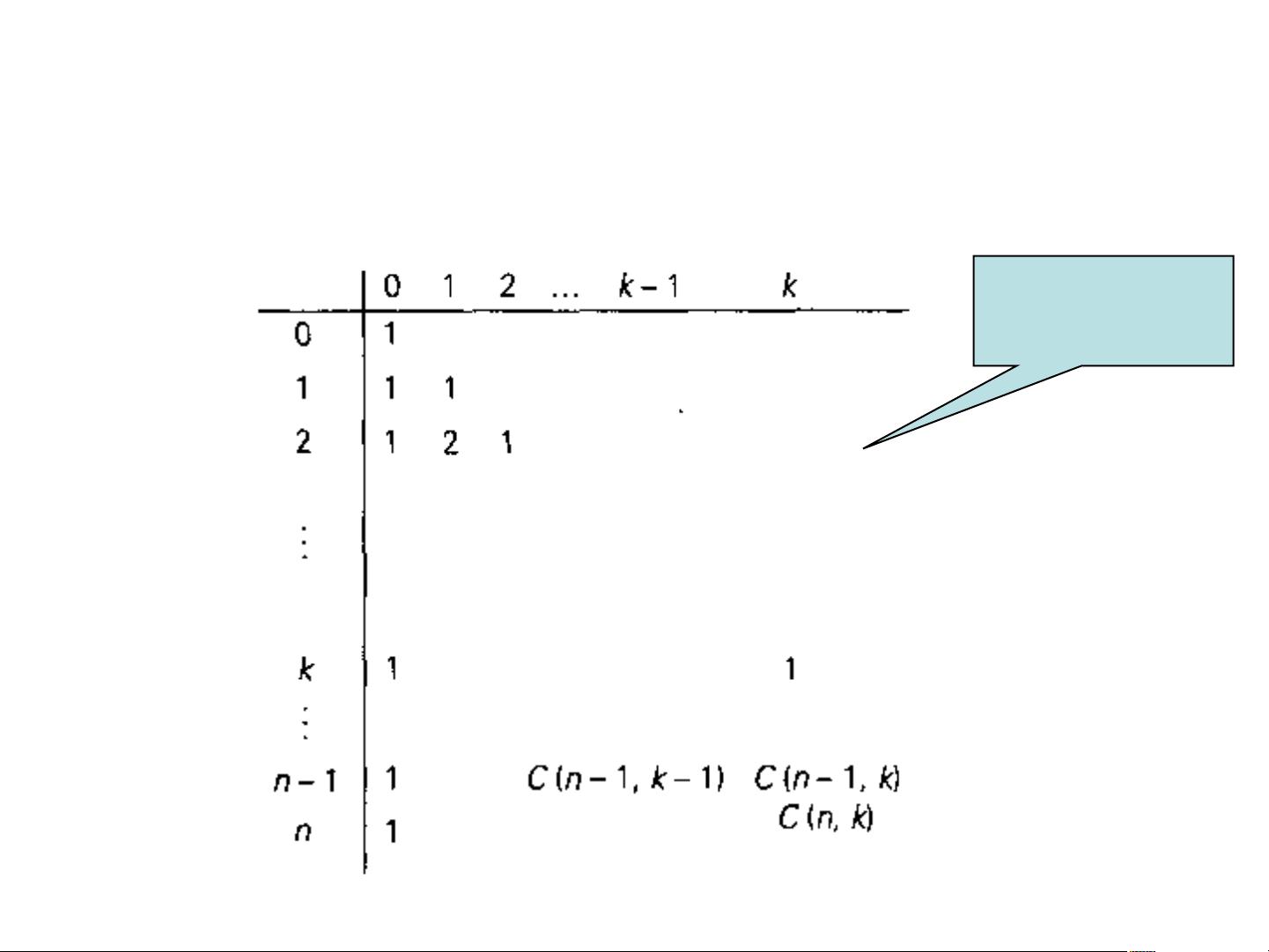 4. 注意事项：动态规划主要针对多阶段最优化问题，如计算二项式系数、Warshall算法、Floyd算法、最优二叉查找树和背包问题等。对于这些问题，动态规划可以避免重复计算，提高效率。 5. 示例应用：课件中提到的特定例子如计算二项式系数、Warshall和Floyd算法（通常用于图论中的最短路径计算）、最优二叉查找树和背包问题（涉及物品选择问题），这些都是动态规划在实际问题中的典型应用。 总结来说，动态规划是一种强大的工具，它通过分解问题、保存中间结果并避免重复工作来解决复杂的问题，尤其在处理具有重叠子问题且满足最优化原理的问题时展现出其价值。理解并掌握动态规划原理对IT专业人员来说至关重要，因为它广泛应用于诸如计算机科学、数据分析和人工智能等领域。