复杂运动目标的三次Chirplet分解逆合成孔径雷达成像
需积分: 10 175 浏览量
更新于2024-08-26
2
收藏 919KB PDF 举报
"这篇研究论文探讨了基于三次Chirplet分解的复杂运动目标的逆合成孔径雷达（ISAR）成像技术。作者包括Yong Wang、Bin Zhao和Yicheng Jiang，他们来自哈尔滨工业大学电子工程技术研究所。文章在2013年12月18日提交，2014年8月6日修订，并于2015年2月4日被接受，发表在IET Synthetic Aperture Radar期刊上，doi编号为10.1049/iet-spr.2014.0086。"
在雷达成像领域，高分辨率的逆合成孔径雷达成像对于具有复杂运动目标的研究是一个重要课题。传统的范围-多普勒算法由于目标复杂运动产生的时变多普勒频移，无法生成清晰聚焦的ISAR图像。为此，该研究提出了一种新的方法来处理这个问题。
论文中，将方位接收信号建模为多成分幅度调制和频率调制（AM-FM）信号。针对这类信号，研究者提出了一种基于广义三次相位函数的三次Chirplet分解新算法，用于对AM-FM信号进行解析分析。Chirplet分解是一种时频分析方法，能够更好地捕捉信号的时间变化和频率变化特性，特别适合处理具有复杂运动特性的目标信号。
通过这个算法，可以更准确地分离和恢复目标的不同运动组件，从而实现对复杂运动目标的精确成像。对应的ISAR成像算法与传统的算法相比，能更好地处理由非线性或随机运动引起的难以预测的多普勒效应，提高成像质量和分辨率。
此外，文章可能还详细阐述了算法的具体步骤、性能分析、仿真结果以及与其他现有方法的比较，以证明所提方法的有效性和优越性。尽管这部分内容没有给出详细细节，但可以推测这些部分会包含对算法的数学描述、实测数据的处理和成像效果的展示，以及可能的未来研究方向。
这篇论文为解决ISAR成像中的复杂运动目标成像问题提供了一个创新的解决方案，利用三次Chirplet分解技术增强了对目标运动状态的捕获和成像质量，对于雷达信号处理和成像技术的发展具有重要的理论和实践意义。
scatterer, η
i,m
is the phase coefficient and
F
i
=−
4
p
l
R
0
, i = 1, 2, ..., Q
h
i,m
=
1
m
V
m−1
· R
i
× r
, i = 1, 2, ..., Q
⎧
⎪
⎨
⎪
⎩
(8)
We can see from (7) that the received signal in a range bin can be
characterised as multi-component AM–FM signal for the complex
motion of the target.
3 Cubic Chirplet decomposition and ISAR
imaging algorithm
3.1 Traditional Chirplet decomposition
The Chirplet decomposition for signal s(t) decomposes it into terms
of well-defined and localised energy components, and consequently
the localised time–frequency variations can be captured for the
signal. The Chirplet atom is defined as follows [28]
g
k
(t) =
1
ps
2
k
4
exp −
(t − t
k
)
2
2
s
2
k
+ j
v
k
(t − t
k
) + j
b
k
(t − t
k
)
2
(9)
where the parameter (t
k
, ω
k
) ∈ R determines the time and frequency
centres for the chirp function, β
k
∈ R denotes the chirp rate and the
variance σ
k
∈ R
+
controls the width for the chirp function. Then,
the signal s(t) can be expressed as
s(t) =
1
k=0
C
k
g
k
(t) (10)
where C
k
is the weighted coefficient.
Some efficient algorithms for the Chirplet decomposition have
recently been proposed, which has been introduced in [34–37].
Here, we consider an example where the Chirplet decomposition is
applied to a signal consisting of two cubic chirps as the form of
(7), and the parameters are shown in Table 1, where t ∈ [ −2s,2s]
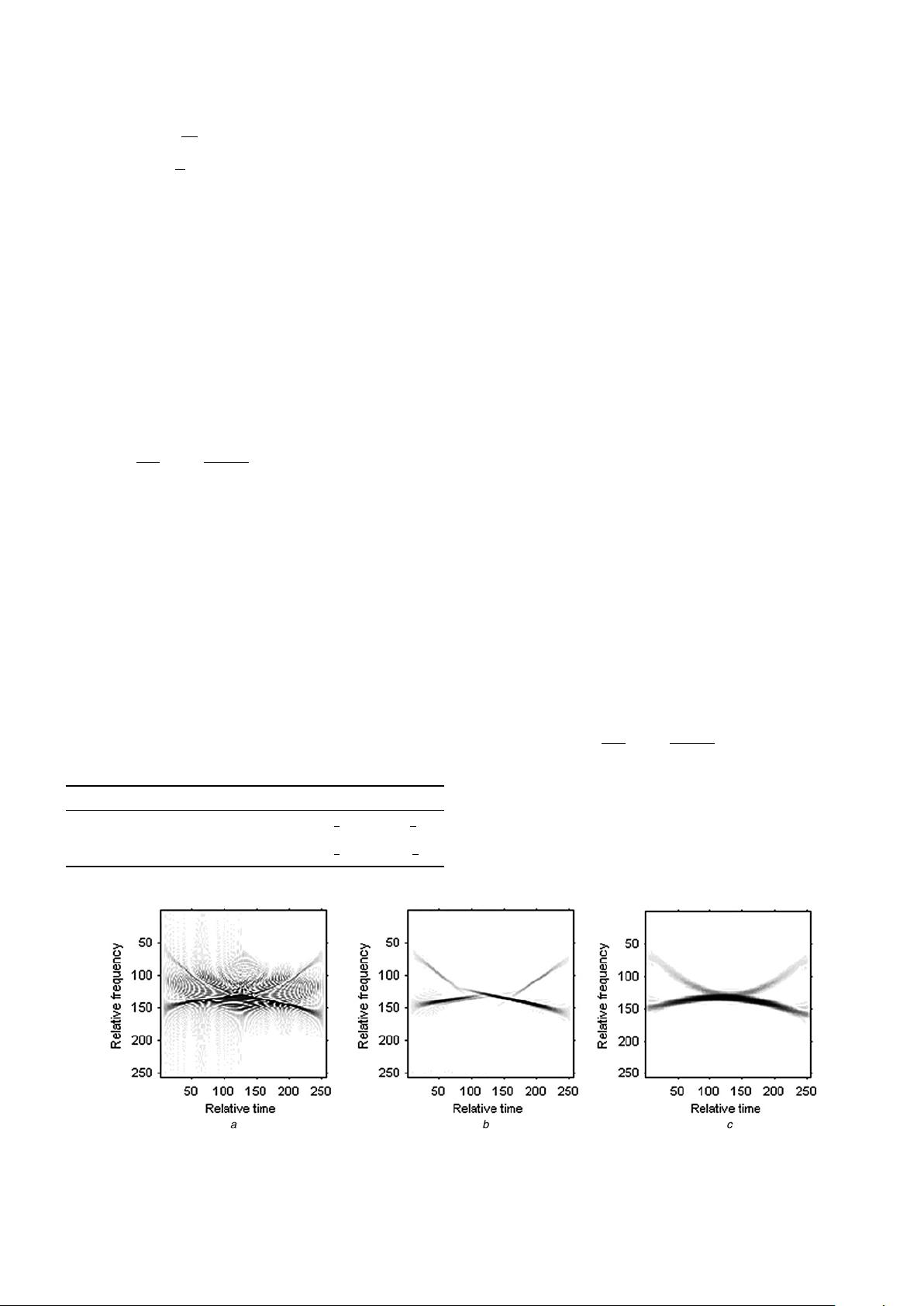
and the sampling frequency is 64 Hz. Fig. 2a is the Wigner–Ville
distribution (WVD) for the signal; Fig. 2b is the WVD after the
Chirplet decomposition. We can see that the Chirplet
decomposition is an efficient way to analyse the multi-component
cubic chirp signals, but the Chirplet atom still has the form of
LFM signal, and cannot characterise the complicated polynomial
phase signals with more accuracy, especially in the joint for the
two Chirplet components.
Remark 1: The WVD is a bilinear TFD [27], and thus it suffers from
the cross-term for multi-component signals. This is obvious in
Fig. 2a, and the auto-term cannot be detected correctly with the
influence of the cross term. After the Chirplet decomposition, the
original signal can be represented as the sum of weighted Chirplet
atoms, as shown in (9) and (10). The Chirplet atom has the form
of a LFM signal with Gaussian envelope, and it can be well
represented by the WVD with optimal time–frequency resolution,
which can be seen from Fig. 2b. Furthermore, the cross-term can
be avoided after the Chirplet decomposition. This is very
significant for the analysis of multi-component signal. The
‘relative time’ and ‘relative frequency’ in Fig. 2 represent the
number of samplings in the time and frequency domains,
respectively, and are not the true values of time and frequency.
In order to improve the analysis performance of multi-component
signals with high non-linear instantaneous frequency trajectories,
such as the aforementioned two-component cubic chirps, the cubic
Chirplet decomposition is more appropriate than the traditional
Chirplet decomposition. The cubic Chirplet atom can match the
complicated signals with high precision, and it is proposed in [38]
as a modified version of Chirplet atom. In this paper, an efficient
algorithm for cubic Chirplet decomposition is proposed, which is
introduced in Section 3.2.
3.2 Cubic Chirplet decomposition
The cubic Chirplet atom is defined as follows by introducing a
curvature parameter γ
k
to the conventional Chirplet atom in [38]
h
k
(t) =
1
ps
2
k
4
exp −
(t − t
k
)
2
2
s
2
k
+ j
v
k
(t − t
k
)
+j
b
k
(t − t
k
)
2
+ j
g
k
(t − t
k
)
3
(11)
Compared with the conventional Chirplet atom in (9), we can notice
that the cubic Chirplet atom consists of further multiplying g
k
(t) with
the term exp[ jγ
k
(t − t
k
)
3
]. The curvature parameter γ
k
has a bending
effect and it is particularly effective to track the evolution against
Table 1 Parameters of the simulated signal
Components (i) A
i
(t) Φ
i
η
i,1
η
i,2
η
i,3
1 2 0 1.2π
1
2
× 2.3
1
3
× 5
2 1 0 0.2π
1
2
× 1.3 −
1
3
× 14
Fig. 2 Time–frequency representations for two-component cubic chirps
a WVD
b WVD after Chirplet decomposition
c RSPWVD after cubic Chirplet decomposition
IET Signal Process., 2015, Vol. 9, Iss. 5, pp. 419–429
421
&
The Institution of Engineering and Technology 2015
剩余10页未读，继续阅读
2021-09-21 上传
189 浏览量
176 浏览量
342 浏览量
142 浏览量
241 浏览量
683 浏览量
101 浏览量
181 浏览量
weixin_38732744
- 粉丝: 4
- 资源: 856
我的内容管理
展开
最新资源
- 通用3C电商网站左侧弹出菜单导航
- 的github
- 智睿企业视频版网站系统 v4.6.0
- 根据vo生成yapi文档：YapiFileGenerattor.zip
- install.zip
- CodeSoft 条形码标签打印开发指南
- GPT-too-AMR2text:复制“ GPT太”的代码
- counterspell:反咒诅咒的 Chrome 扩展
- CodingTestPractice
- 点文件
- 企业文化竞争（6个文件）
- pytorch-pruning.zip
- 天猫左侧导航菜单分类列表
- torch_sparse-0.6.1-cp36-cp36m-win_amd64whl.zip
- SiamSE:“比例等方差可改善连体跟踪”的代码
- BakedModpack：冒雨风险的modpack 2
