二阶巴特沃兹有源低通滤波器设计与仿真

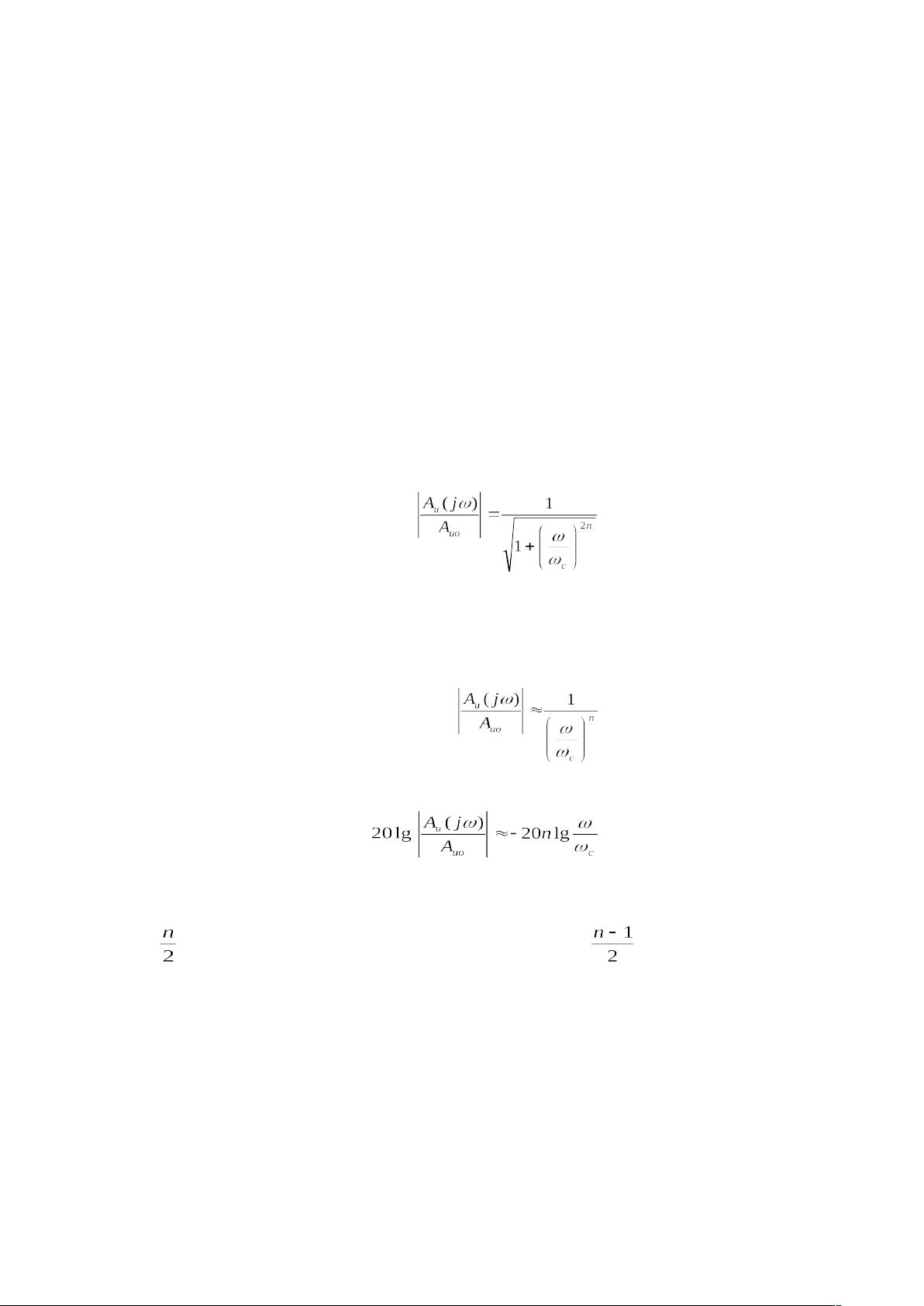
"本文主要介绍了巴特沃兹有源低通滤波器的设计方法和实例，涉及二阶滤波器的频率特性和设计步骤，并提供了一个具体的设计案例，旨在实现特定的滤波性能指标。" 在电子工程领域，低通滤波器（LPF）是一种重要的信号处理工具，用于去除高频噪声，保留低频信号。巴特沃兹滤波器以其平滑的滚降特性而被广泛采用，特别是有源低通滤波器，由于引入了运算放大器，可以提供更好的增益稳定性和线性特性。本文关注的是二阶巴特沃兹有源低通滤波器的设计。 首先，巴特沃兹低通滤波器的幅频特性是其核心特征，公式（1）展示了其与频率的关系。当频率为零时，滤波器输出电压最大，随着频率增加，电压放大倍数会逐渐下降，当频率达到截止角频率ωc时，输出电压衰减至最大值的一半（-3dB）。公式（2）和（3）揭示了高阶滤波器的阻带衰减速率，通常为20ndB/十倍频或6ndB/倍频。这意味着滤波器的阶数越高，衰减速度越快，滤波效果越好。 设计二阶巴特沃兹有源低通滤波器通常包括以下步骤： 1. 确定滤波器阶数n，这将直接影响滤波器的滚降速率和阻带衰减。 2. 选择适合的电路形式，如Sallen-Key电路，这种电路结构简单且易于分析。 3. 建立传递函数的系数方程组，这基于所需的频率响应特性。 4. 解方程组计算出电路中的电阻、电容和运算放大器的参数。 5. 实物组装电路并进行调试，确保实际性能符合设计指标。 在设计实例中，设定了一个具体的目标：截止频率fC=1kHz，通带电压放大倍数Auo=2，且在10倍截止频率时要求衰减超过30dB。通过计算和选择，可以确定滤波器的阶数为2，并选用Sallen-Key电路作为电路结构。通过解方程组，可以得出电路中电阻和电容的具体值，从而构建出满足要求的滤波器。 巴特沃兹有源低通滤波器的设计涉及到信号处理理论、电路分析以及数值计算。通过精确的元件选择和电路配置，可以实现对不同频率信号的有效筛选和处理，这对于通信系统、音频设备和各种信号检测应用具有重要意义。