概率论与随机过程：电气与计算机工程师基础教程

需积分: 32 31 浏览量更新于2024-07-17 收藏 5.98MB PDF 举报

"这是一本适合电气与计算机工程师的入门概率论教材，涵盖了从基础概率知识到随机过程的全面内容。" 《概率论与随机过程在电气与计算机工程中的应用》是一本面向电气与计算机工程学生的专业教材。这本书的编写旨在帮助学生理解和应用概率论这一强大的工具，以解决他们在技术开发中遇到的问题。书中从高级本科阶段的知识开始，只需要读者具备一定的概率基础知识，然后逐步深入到研究生阶段更复杂的主题。前五章主要介绍概率论的基础知识，包括离散和连续随机变量的概念。离散随机变量通常涉及到可以计数的事件，如掷骰子的结果；而连续随机变量则涉及连续范围内的数值，如温度读数。这些章节会讲解概率的基本规则、条件概率、独立事件、期望值、方差等概念，以及如何处理单个和多个随机变量的概率分布。接下来的章节则专注于更专业的领域，如随机向量、高斯随机向量（即正态分布的多维扩展）、随机过程、马尔可夫链和收敛性。随机向量涉及多个随机变量的联合分布，而高斯随机向量在信号处理和统计中尤其重要。随机过程是研究随时间变化的随机现象，例如股票价格的变化或无线通信中的噪声。马尔可夫链则用于描述状态之间转移的概率，常应用于预测和建模。收敛性则是研究随机变量序列随时间趋于稳定性的理论。这本书包含超过300个详尽的例题和大约800个家庭作业问题，这对于学生巩固理论知识和提升实践能力大有裨益。此外，还有专门的复习部分，有助于准备考试。这不仅是一本教科书，也是从事通信、信号处理和计算机网络流量分析的研究人员的重要参考书。除了正文内容，该书还提供了额外的资源，如习题答案，这些辅助材料进一步增强了学习体验，确保学生能够充分理解和应用所学知识。这本书是进阶本科生和研究生的理想教材，也是概率论与随机过程领域专业人士的宝贵参考资料。

2 Introduction to probability

−1

0.5

Figure 1.2. Matched ﬁlter input (top) in which the signal is hidden by noise. Matched ﬁlter output (bottom) in

which the signal presence is obvious.

Optical communication systems. Optical communication systems use photodetectors

(see Figure 1.3) to interface between optical and electronic subsystems. When these sys-

detector

photo−

photoelectrons

light

Figure 1.3. Block diagram of a photodetector. The rate at which photoelectrons are produced is proportional to

the intensity of the light.

tems are at the limits of their operating capabilities, the number of photoelectrons produced

by the photodetector is well-modeled by the Poisson

random variable you will study in

Chapter 2 (see also the Poisson process in Chapter 11). In deciding whether a transmitted

bit is a zero or a one, the receiver counts the number of photoelectrons and compares it

to a threshold. System performance is determined by computing the probability that the

threshold is exceeded.

Wireless communication systems. In order to enhance weak signals and maximize the

range of communication systems, it is necessary to use ampliﬁers. Unfortunately, ampliﬁers

always generate thermal noise, which is added to the desired signal. As a consequence of the

underlying physics, the noise is Gaussian. Hence, the Gaussian density function, which you

will meet in Chapter 4, plays a prominent role in the analysis and design of communication

systems. When noncoherent receivers are used, e.g., noncoherent frequency shift keying,

Many important quantities in probability and statistics are named after famous mathematicians and

statisticians. You can use an Internet search engine to ﬁnd pictures and biographies of them on

the web. At the time of this writing, numerous biographies of famous mathematicians and statisti-

cians can be found at http://turnbull.mcs.st-and.ac.uk/history/BiogIndex.html and at

http://www.york.ac.uk/depts/maths/histstat/people/welcome.htm. Pictures on stamps

and currency can be found at http://jeff560.tripod.com/.

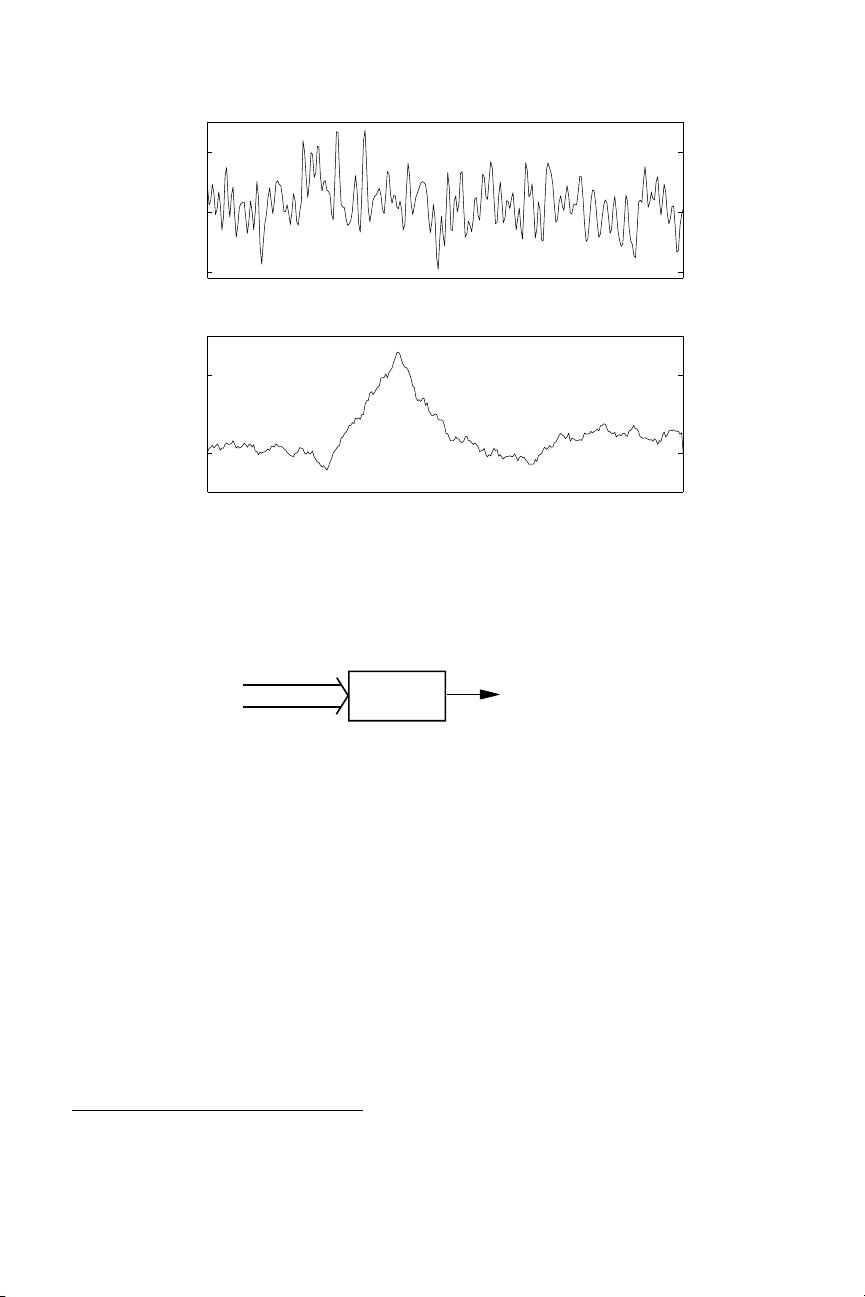
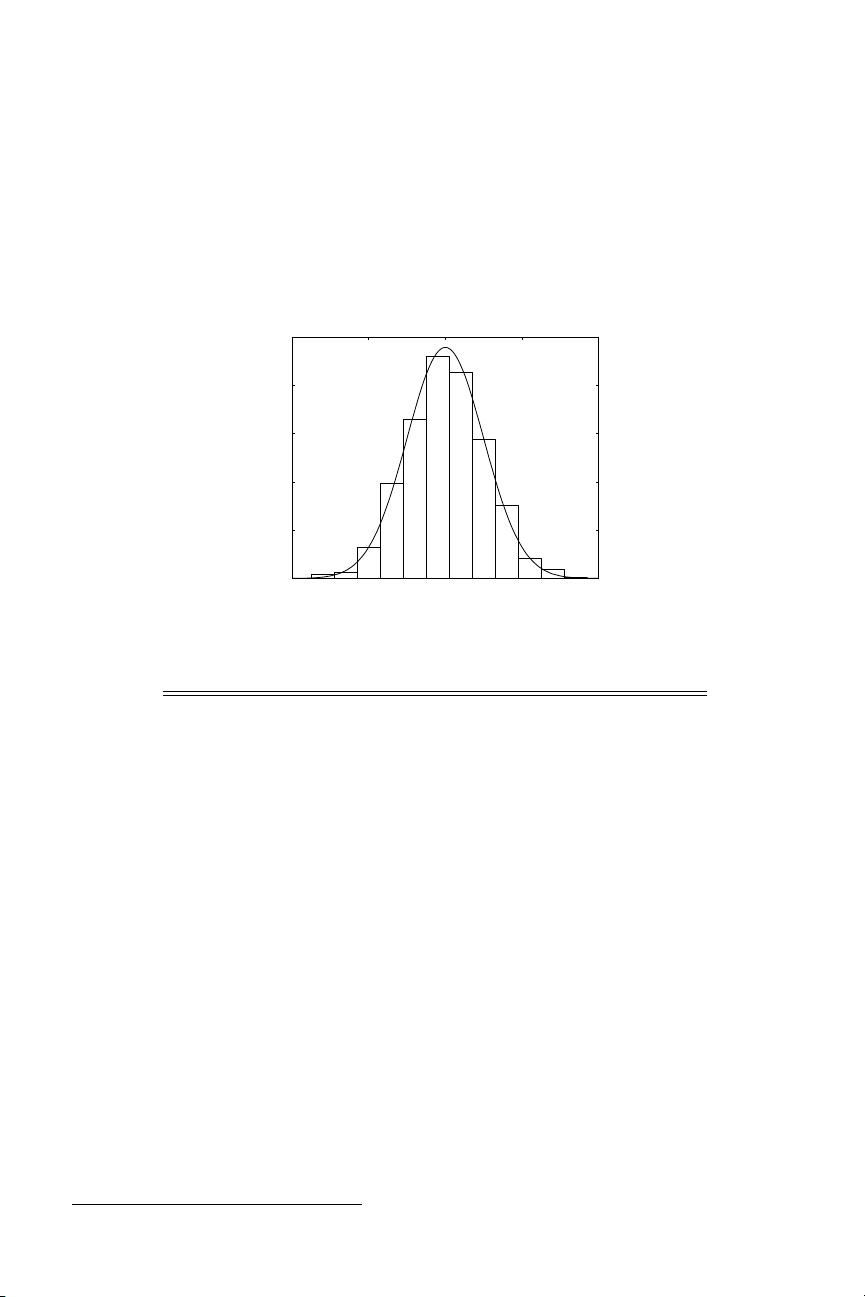
Relative frequency 3

this naturally leads to the Rayleigh, chi-squared, noncentral chi-squared, and Rice density

functions that you will meet in the problems in Chapters 4, 5, 7, and 9.

Variability in electronic circuits. Although circuit manufacturing processes attempt to

ensure that all items have nominal parameter values, there is always some variation among

items. How can we estimate the average values in a batch of items without testing all of

them? How good is our estimate? You will learn how to do this in Chapter 6 when you

study parameter estimation and conﬁdence intervals. Incidentally, the same concepts apply

to the prediction of presidential elections by surveying only a few voters.

Computer network trafﬁc. Prior to the 1990s, network analysis and design was carried

out using long-established Markovian models [41, p. 1]. You will study Markov chains

in Chapter 12. As self similarity was observed in the trafﬁc of local-area networks [35],

wide-area networks [43], and in World Wide Web trafﬁc [13], a great research effort began

to examine the impact of self similarity on network analysis and design. This research has

yielded some surprising insights into questions about buffer size vs. bandwidth, multiple-

time-scale congestion control, connection duration prediction, and other issues [41, pp. 9–

11]. In Chapter 15 you will be introduced to self similarity and related concepts.

In spite of the foregoing applications, probability was not originally developed to handle

problems in electrical and computer engineering. The ﬁrst applications of probability were

to questions about gambling posed to Pascal in 1654 by the Chevalier de Mere. Later,

probability theory was applied to the determination of life expectancies and life-insurance

premiums, the theory of measurement errors, and to statistical mechanics. Today, the theory

of probability and statistics is used in many other ﬁelds, such as economics, ﬁnance, medical

treatment and drug studies, manufacturing quality control, public opinion surveys, etc.

Relative frequency

Consider an experiment that can result in M possible outcomes, O

,...,O

.Forex-

ample, in tossing a die, one of the six sides will land facing up. We could let O

denote

the outcome that the ith side faces up, i = 1,...,6. Alternatively, we might have a computer

with six processors, and O

could denote the outcome that a program or thread is assigned to

the ith processor. As another example, there are M = 52 possible outcomes if we draw one

card from a deck of playing cards. Similarly, there are M = 52 outcomes if we ask which

week during the next year the stock market will go up the most. The simplest example we

consider is the ﬂipping of a coin. In this case there are two possible outcomes, “heads” and

“tails.” Similarly, there are two outcomes when we ask whether or not a bit was correctly

received over a digital communication system. No matter what the experiment, suppose

we perform it n times and make a note of how many times each outcome occurred. Each

performance of the experiment is called a trial.

Let N

) denote the number of times O

occurred in n trials. The relative frequency of outcome O

)

is the fraction of times O

occurred.

When there are only two outcomes, the repeated experiments are called Bernoulli trials.

What is probability theory? 5

1000

)+N

1000

)+N

1000

)=76

1000

)+N

1000

)+N

1000

)=21

1000

)+N

1000

)+N

1000

)=9

1000

)+N

1000

)+N

1000

)=1.

This summary is illustrated in the histogram shown in Figure 1.4. (The bars are centered

over values of the form k/100; e.g., the bar of height 230 is centered over 0.49.)

0.3 0.4 0.5 0.6 0.7

100

150

200

250

Figure 1.4. Histogram of Example 1.2 with overlay of a Gaussian density.

Below we give an indication of why most of the time the relative frequency of heads is

close to one half and why the bell-shaped curve ﬁts so well over the histogram. For now

we point out that the foregoing methods allow us to determine the bit-error rate of a digital

communication system, whether it is a wireless phone or a cable modem connection. In

principle, we simply send a large number of bits over the channel and ﬁnd out what fraction

were received incorrectly. This gives an estimate of the bit-error rate. To see how good an

estimate it is, we repeat the procedure many times and make a histogram of our estimates.

What is probability theory?

Axiomatic probability theory, which is the subject of this book, was developed by A.

N. Kolmogorov

in 1933. This theory speciﬁes a set of axioms for a well-deﬁned math-

ematical model of physical experiments whose outcomes exhibit random variability each

time they are performed. The advantage of using a model rather than performing an exper-

iment itself is that it is usually much more efﬁcient in terms of time and money to analyze

a mathematical model. This is a sensible approach only if the model correctly predicts the

behavior of actual experiments. This is indeed the case for Kolmogorov’s theory.

A simple prediction of Kolmogorov’s theory arises in the mathematical model for the

relative frequency of heads in n tosses of a fair coin that we considered in Example 1.1. In

the model of this experiment, the relative frequency converges to 1/2asn tends to inﬁnity;

The website http://kolmogorov.com/ is devoted to Kolmogorov.

6 Introduction to probability

this is a special case of the the strong law of large numbers, which is derived in Chapter 14.

(A related result, known as the weak law of large numbers, is derived in Chapter 3.)

Another prediction of Kolmogorov’s theory arises in modeling the situation in Exam-

ple 1.2. The theory explains why the histogram in Figure 1.4 agrees with the bell-shaped

curve overlaying it. In the model, the strong law tells us that for each k, the relative fre-

quency of having exactly k heads in 100 tosses should be close to

100!

k!(100 −k)!

100

Then, by the central limit theorem, which is derived in Chapter 5, the above expression is

approximately equal to (see Example 5.19)

√

exp

−

k −50

(You should convince yourself that the graph of e

−x

is indeed a bell-shaped curve.)

Because Kolmogorov’s theory makes predictions that agree with physical experiments,

it has enjoyed great success in the analysis and design of real-world systems.

1.1 Sample spaces, outcomes, and events

Sample spaces

To model systems that yield uncertain or random measurements, we let Ω denote the

set of all possible distinct, indecomposable measurements that could be observed. The set

Ω is called the sample space. Here are some examples corresponding to the applications

discussed at the beginning of the chapter.

Signal processing. In a radar system, the voltage of a noise waveform at time t can be

viewed as possibly being any real number. The ﬁrst step in modeling such a noise voltage

is to consider the sample space consisting of all real numbers, i.e., Ω =(−∞, ∞).

Computer memories. Suppose we store an n-bit word consisting of all 0s at a particular

location. When we read it back, we may not get all 0s. In fact, any n-bit word may be read

out if the memory location is faulty. The set of all possible n-bit words can be modeled by

the sample space

Ω = {(b

,...,b

) : b

= 0or1}.

Optical communication systems. Since the output of a photodetector is a random

number of photoelectrons. The logical sample space here is the nonnegative integers,

Ω = {0,1,2,...}.

Notice that we include 0 to account for the possibility that no photoelectrons are observed.

Wireless communication systems. Noncoherent receivers measure the energy of the

incoming waveform. Since energy is a nonnegative quantity, we model it with the sample

space consisting of the nonnegative real numbers, Ω =[0, ∞).

Variability in electronic circuits. Consider the lowpass RC ﬁlter shown in Figure 1.5(a).

Suppose that the exact values of R and C are not perfectly controlled by the manufacturing

process, but are known to satisfy

95 ohms ≤ R ≤ 105 ohms and 300

F ≤ C ≤ 340

剩余641页未读，继续阅读

紫曦�

粉丝: 1
资源: 1

概率论与随机过程：电气与计算机工程师基础教程

wx494社区门诊管理系统小程序-php+vue+uniapp.zip（可运行源码+sql文件+文档）

Probability, Statistics, and Random Processes For Electrical Engineering

Probability, Statistics, and Random Processes for Electrical Engineering 答案

Probability & Random Processes for Electrical and Computer Engineers

Gubner J.A. - Probability and Random Processes for Electrical and Computer Engineers (Cambridge University Press, 2006)

probability statistics and random processes for electrical engineers 答案

Solution of Probability And Random Processes For ECE Engineers

Probability and Random Processes

Probability and Random processes

Intuitive Probability and Random Processes

最新资源