编程艺术揭秘：矩阵与线性方程的深度解析

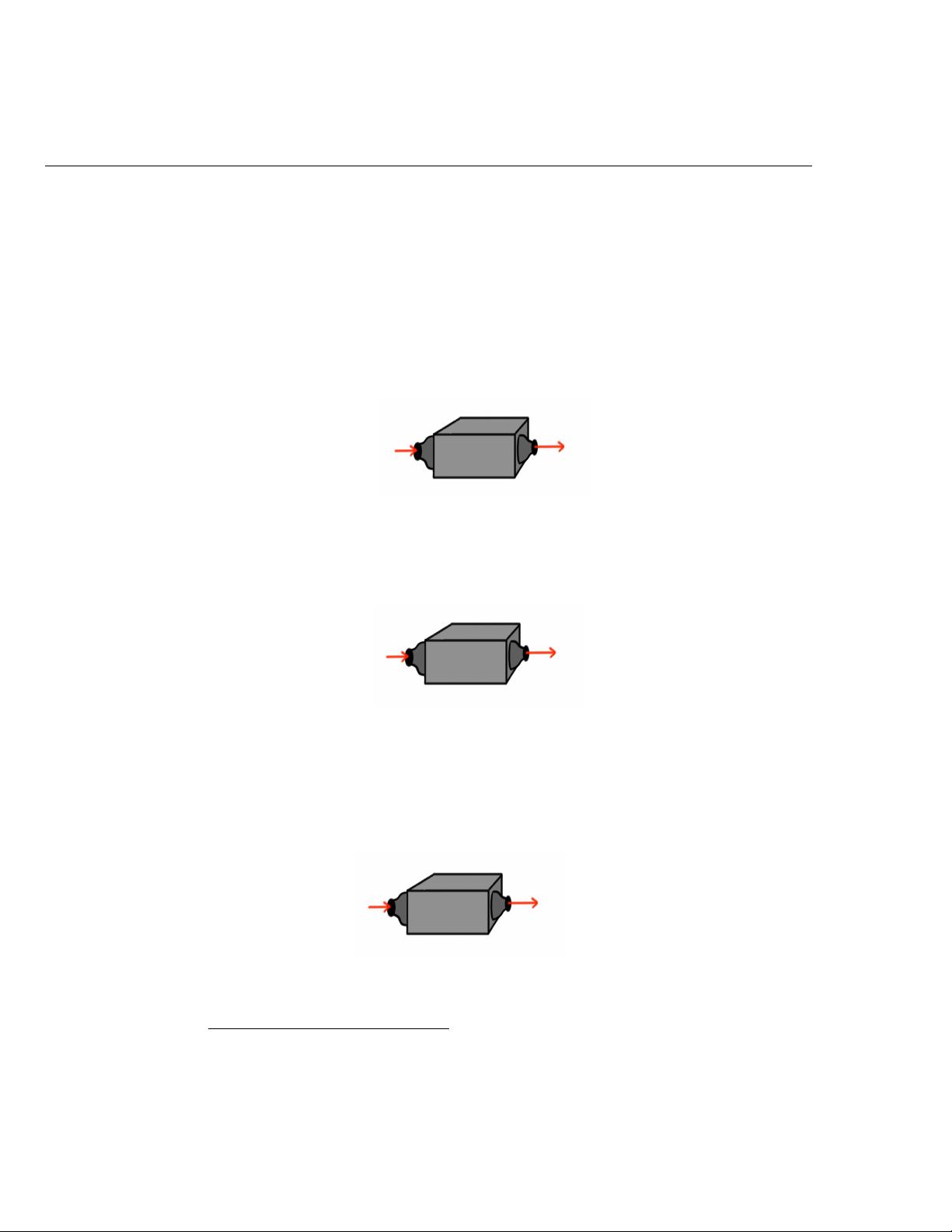
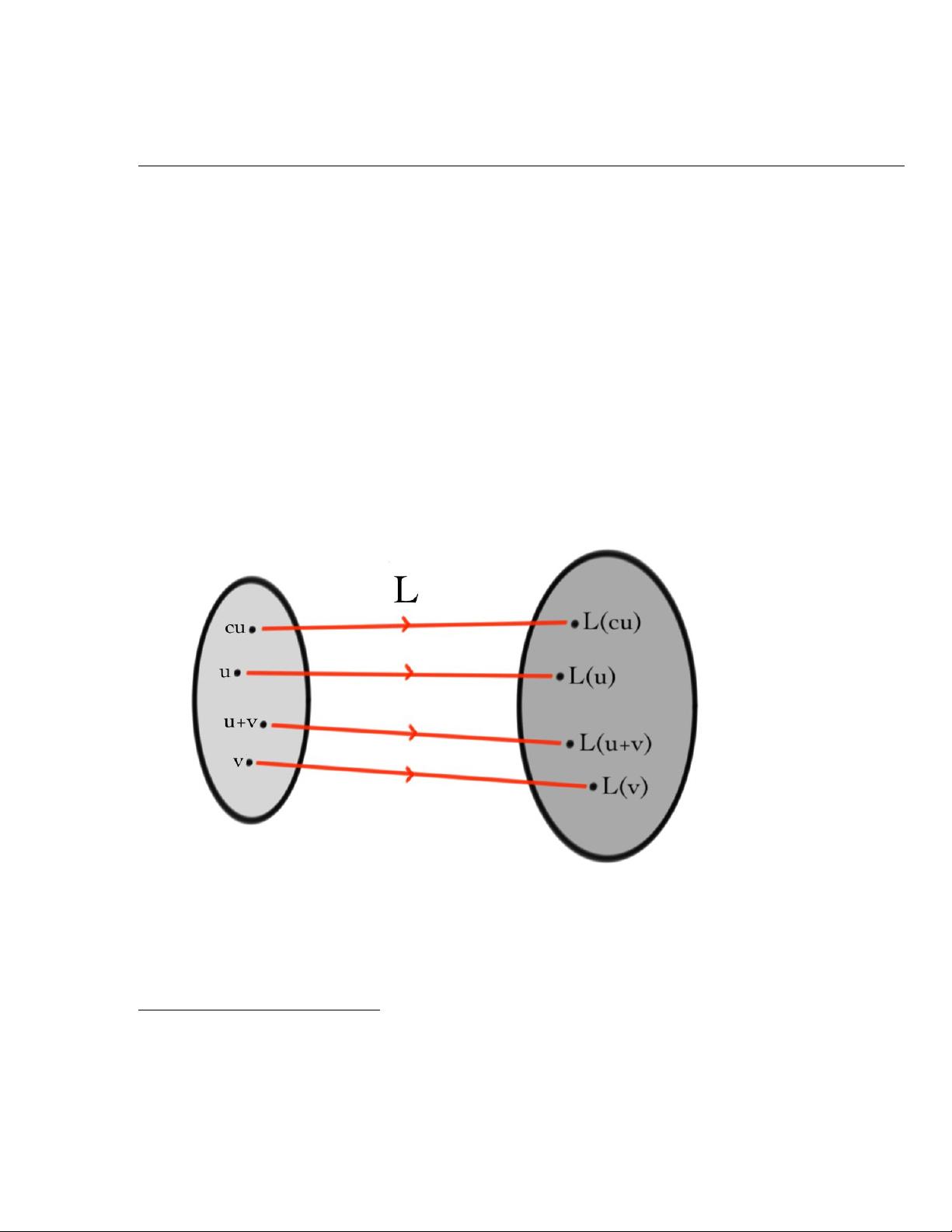
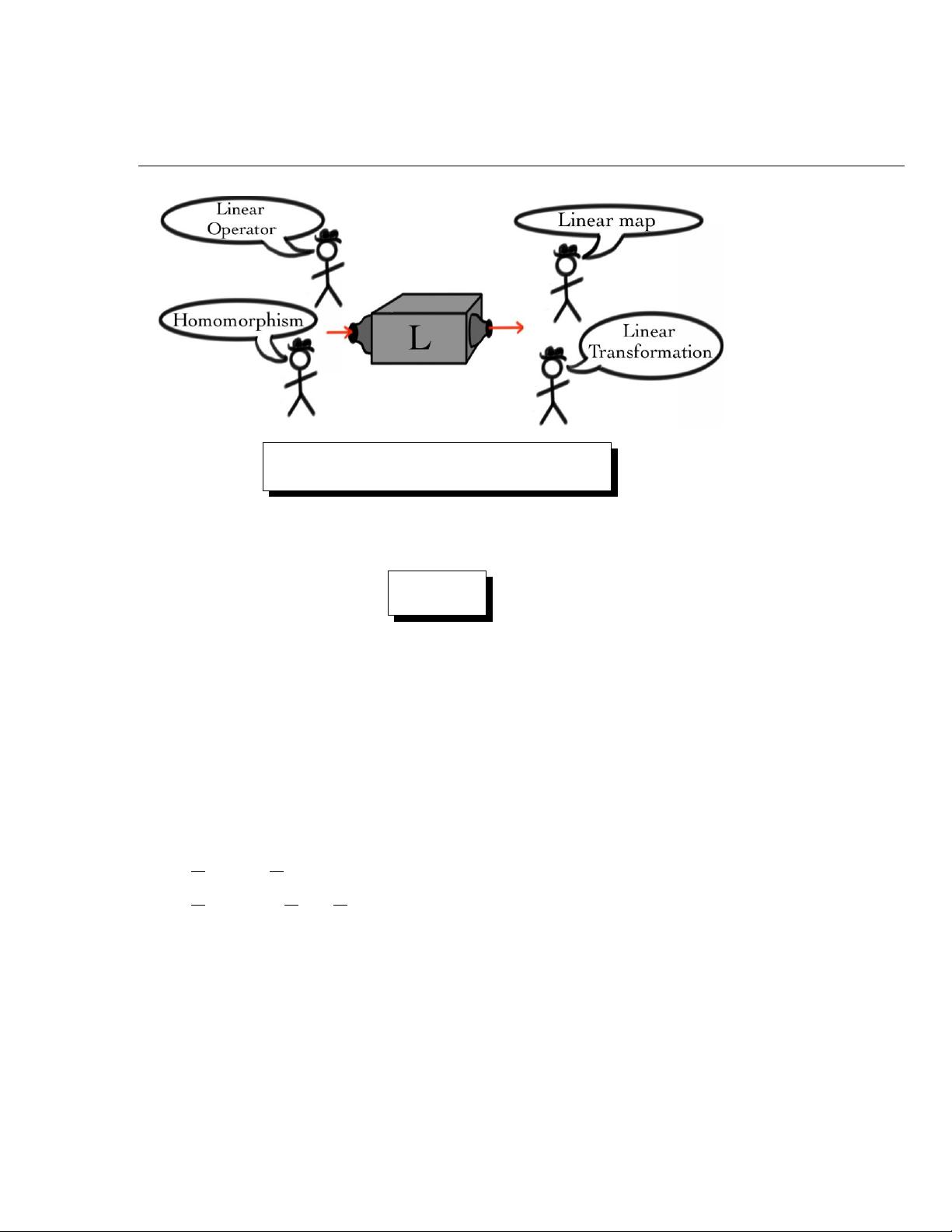
"编程艺术美"是一本深入浅出的计算机编程指南，特别关注于线性代数这一核心主题，由David Cherney、Tom Denton、Rohit Thomas和Andrew Waldron共同编著，并在Katrina Glaeser和Travis Scrimshaw的编辑下，于2013年首次出版。本书遵循Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License授权，旨在帮助读者理解并掌握编程中的关键概念。 第一章“什么是线性代数？”首先介绍了组织信息的基本概念，阐述了向量在编程中的应用。向量是编程中处理数据的重要工具，它们可以表示多维数据集，用于表示和操作数据方向与数量的关系。接着，章节探讨了线性函数，这些函数关系通常是多项式或简单的加权和，对于理解和解决线性问题至关重要。 矩阵作为线性代数的核心概念，被详细解释。1.4节专门讲解矩阵乘法，它被比喻为函数的复合，有助于理解多个变换如何组合成单一操作。随后，"矩阵迷宫"可能是指通过矩阵来探索和理解复杂系统的一种隐喻，引导读者从不同角度探索矩阵的性质和运算。 第二章聚焦于线性方程组，包括高斯消元法，这是一种求解线性系统的标准算法。作者首先介绍augmented matrix（增广矩阵）的表示方式，然后强调等价性和解方程的过程。通过将矩阵转换到行最简形（Reduced Row Echelon Form, RREF），可以清晰地识别出解的存在和唯一性。此外，元素行操作（Elementary Row Operations, EROs）的讨论深入到矩阵操作和其在解方程中的运用，如LU、LUD和PLDU分解。 第三章和第四章内容未在提供的部分给出，但可以推测，这部分可能会进一步扩展线性代数在编程中的实际应用，例如在解决大规模数据处理问题、机器学习模型中的特征变换、以及图形学中的矩阵变换等方面。同时，可能会介绍如何利用线性代数原理优化代码性能，提升算法效率。 “编程艺术美”不仅仅局限于基础的线性代数概念，还强调了如何将这些理论应用于实际编程场景，帮助读者在编写高效、可读性强的代码时，更好地理解和利用线性代数的力量，从而提升编程艺术。每一章都包含复习问题，以便读者检验理解并加深记忆。无论是初学者还是经验丰富的程序员，这本教材都能提供深入且实用的学习资源。