解决异或问题的双层神经网络与反向传播优化策略

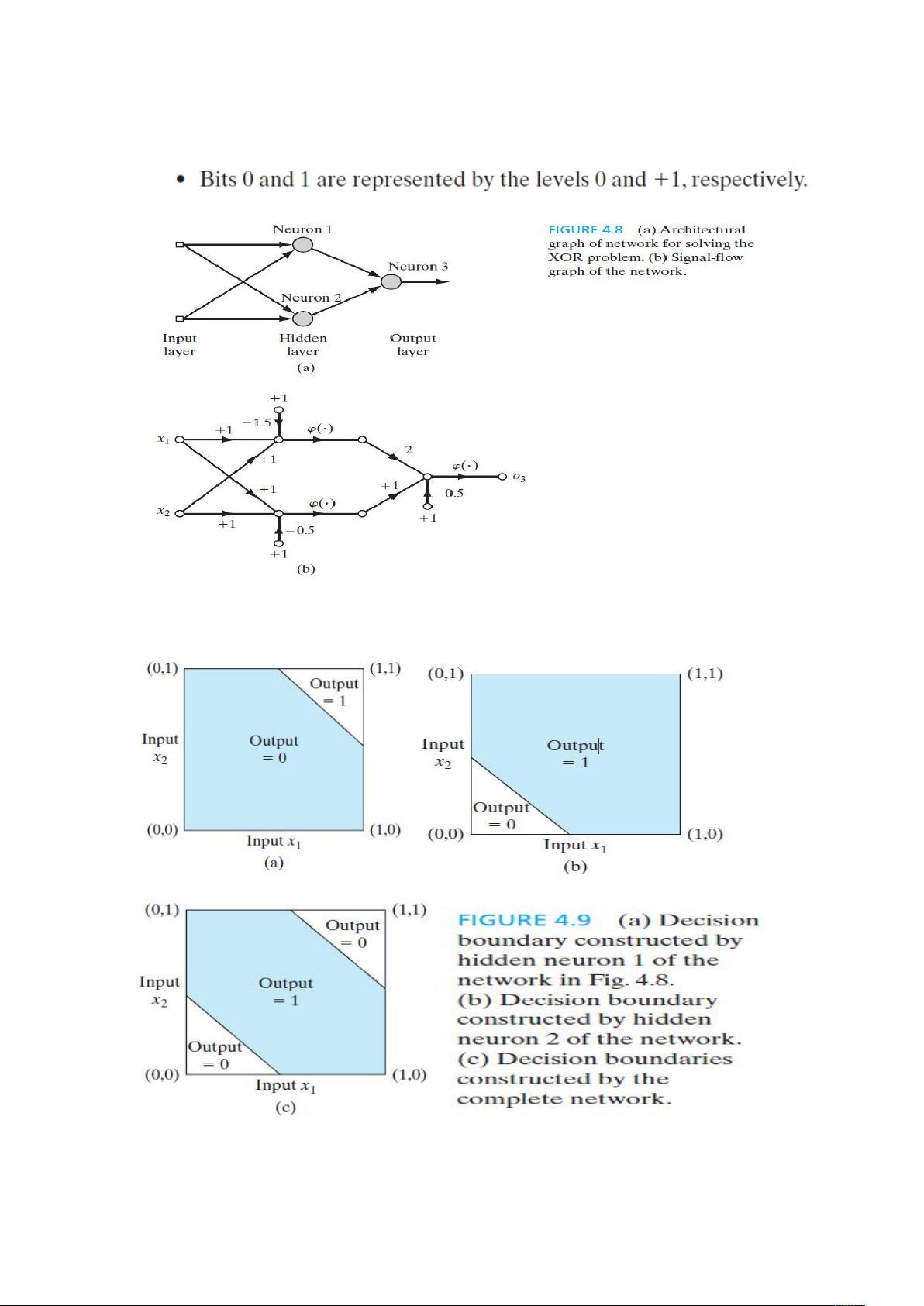
"本资源主要聚焦于机器学习领域的神经网络讲解，特别是针对异或问题（XOR）的讨论。异或问题是一个典型的非线性可分问题，传统的单层感知器由于决策边界只能是线性的，无法解决这种问题。然而，通过引入隐藏层，特别是使用具有两个神经元的隐藏层，可以利用McCulloch-Pitts模型和特定的激活函数，如S函数，解决异或问题。S函数作为奇函数有助于提高学习速度，并要求输出层神经元的期望响应与sigmoid函数的极限值保持一定偏离，避免神经元饱和导致的学习过程减缓。 优化反向传播算法的部分方法包括随机和批量更新权重、最大化信息内容、以及选择合适的激活函数。激活函数的选择需考虑学习速度，如使用自变量为奇函数的S函数。输入值的标准化有助于稳定网络表现，而恰当的初始化策略对于突触权值的设置至关重要，例如采用双曲正切函数时，应确保初始值落在sigmoid函数的线性部分和饱和部分之间的过渡区域。 此外，资源还涉及计算机实验，如模式分类和反向传播算法的实际应用，以及如何将多层感知器表示为离散参数和权值向量。Hessian矩阵等相关概念也可能在这部分进行介绍，展示了神经网络训练过程中的数学基础和优化技巧。这份资料为机器学习爱好者提供了深入了解神经网络特别是解决复杂问题如异或问题的方法和策略。"