图论讲解:Dijkstra算法求最短路径
需积分: 0 178 浏览量
更新于2024-07-01
收藏 922KB PDF 举报
"该资源主要介绍了图论中的最短路径问题,特别是带权有向图的最短路径。内容涵盖图的基本定义、存储结构、遍历、连通性以及有向无环图的应用。核心是Dijkstra算法,用于按路径长度递增顺序生成最短路径。"
在计算机科学和图论中,图是一种抽象的数据结构,它由顶点和边构成,用来表示对象之间的关系。在第七章中,讲解了图的各种概念,包括:
1. **图的定义和术语**:图由顶点(节点)和边(连接顶点的线)组成,可以是有向的(边有方向)或无向的(边无方向)。边可能带有权重,表示某种度量,如距离、成本或时间。
2. **图的存储结构**:常用的存储结构有邻接矩阵和邻接表,前者用二维数组表示每个顶点的相邻顶点,后者则用链表记录每个顶点的邻接关系,节省空间。
3. **图的遍历**:包括深度优先搜索(DFS)和广度优先搜索(BFS),用于访问图的所有顶点,DFS常用于寻找连通性,BFS则常用于求最短路径。
4. **图的连通**:图的连通性关注图中是否存在从任意顶点到其他任意顶点的路径,无环连通图可以是树形结构。
5. **有向无环图(DAG)及其应用**:DAG在许多领域都有应用,例如任务调度、数据流分析等,它们没有形成循环的边,因此不存在回路。
6. **最短路径**:这是图论中的一个重要问题,特别是对于交通网络,找到两点间的最短路径至关重要。最短路径不仅考虑路径的存在,还涉及权值最小的路径选择。
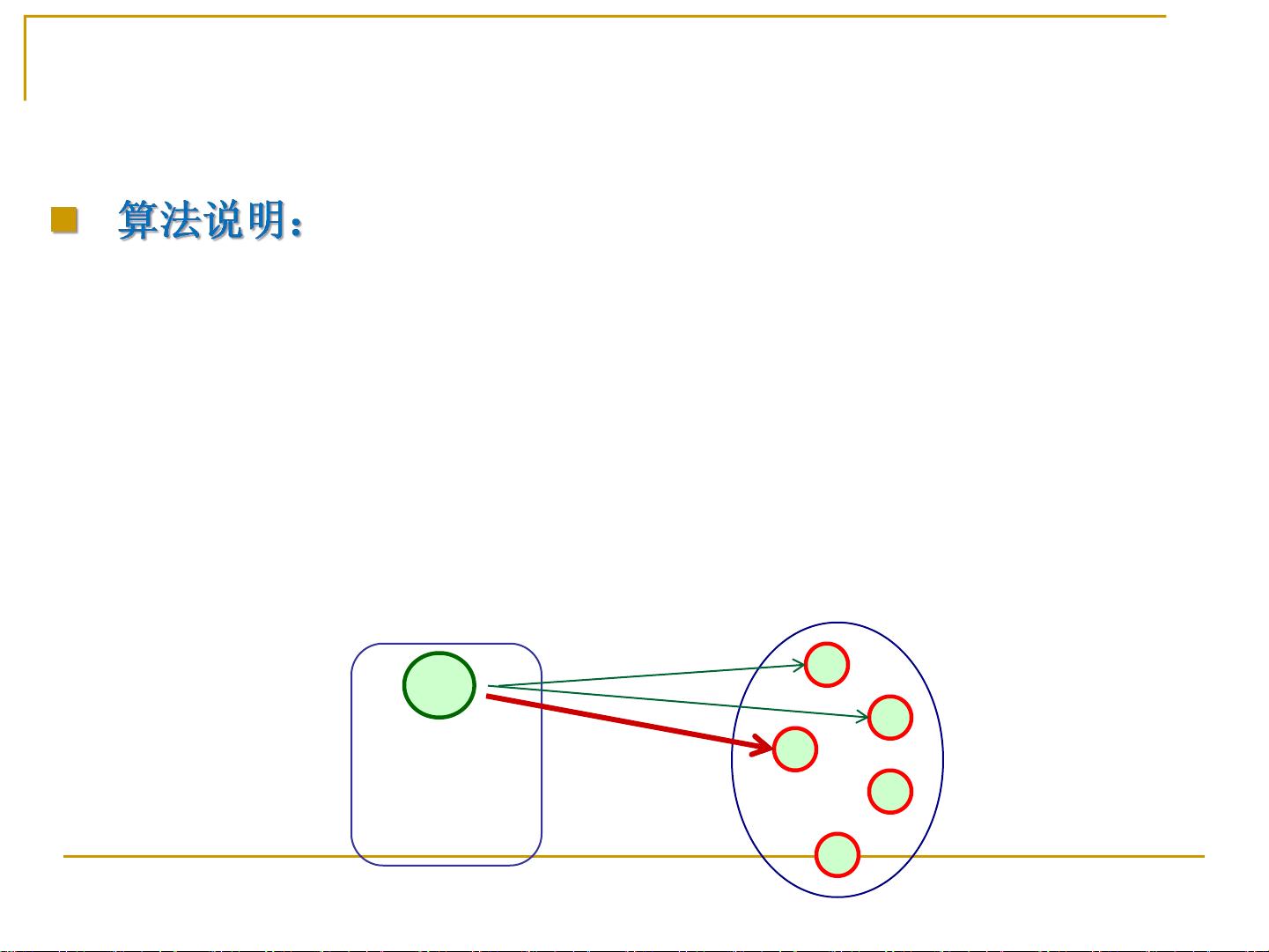
Dijkstra算法是解决单源最短路径问题的著名算法,由Edsger Dijkstra提出。算法的核心思想是逐步扩大已知最短路径的顶点集合S,同时维护一个未处理顶点集合V-S,通过不断更新路径长度来确保每次加入S的顶点对应当前最短路径。Dijkstra算法使用一个优先队列(通常用最小堆实现)来按照路径长度递增的顺序处理顶点,每次从队列中取出具有最短路径的顶点u,然后更新与u相邻的未处理顶点Vj的最短路径。
在Dijkstra算法中,每一步都会比较当前已知的源点到顶点Vj的最短路径和经过u的新路径,如果新路径更短,则更新最短路径。这个过程持续到所有顶点都被处理,即找到了从源点到所有其他顶点的最短路径。
总结来说,本资源详细介绍了图的理论基础和最短路径问题,特别是Dijkstra算法的原理和步骤,对理解和解决实际问题如网络路由、交通规划等具有重要价值。
2018-06-15 上传
2010-11-09 上传
2018-03-30 上传
2011-11-04 上传
2022-01-02 上传
2021-07-15 上传
2013-07-17 上传
陈后主
- 粉丝: 39
- 资源: 340
最新资源
- 血色素沉着病:混合了性别和基因型的血液样本具有铁血毒性
- 参考资料-基于soc单片机的ph值检测与控制.zip
- Copy Tab-crx插件
- pandas_flavor-0.1.2.tar.gz
- Tcldrop-开源
- zTail-开源
- 通往软件架构师的道路-Python开发
- Laboratorio7_CVDS
- 恶意软件收集:计算机的恶意软件,压力测试等的源代码
- whiteboard-angular-client:白板前端。 Whiteboard Web App的Angular客户端。 :books:
- pandas_flavor-0.1.1.tar.gz
- iTab - Awesome Tab Manager-crx插件
- aria2c-android-app:aria2c-android-app
- projecting
- x70talk-开源
- DPDraggableButton-Swift:拖动或点击按钮以触发手势事件