OFDM系统中定时同步误差影响的数学分析

需积分: 3 45 浏览量更新于2024-09-16 收藏 246KB PDF 举报

"该资源是一篇关于OFDM系统中定时同步误差影响的数学分析的论文，发表在2006年的IEEE Transactions on Communications期刊上。文章探讨了定时同步错误如何导致OFDM系统的性能下降，包括引入的交调干扰(ICI)和符号间干扰(ISI)，并分析了这些错误可能源于初始帧同步错误或信道功率延迟剖面的变化。作者提供了数学模型来量化频率选择性衰落环境中定时误差对OFDM接收机性能的影响，计算了干扰项的功率以及平均信号与干扰比，并扩展到亚采样级别，揭示了定时误差对OFDM系统性能的非对称效应。此外，文中还包括了模拟结果来验证理论分析。" 在OFDM（正交频分复用）技术中，定时同步是确保正确解调各个子载波的关键环节。当存在定时同步误差时，它可能导致以下两个主要问题： 1. **交调干扰(Inter-Carrier Interference, ICI)**：由于OFDM系统将数据分配到多个正交子载波上，即使是很小的定时误差也可能导致一个子载波的信号泄漏到相邻的子载波，从而产生ICI。这种干扰会破坏子载波间的正交性，降低系统的频谱效率。 2. **符号间干扰(Inter-Symbol Interference, ISI)**：定时误差可能导致符号的起始和结束时间错位，从而在接收端引起ISI。在频率选择性衰落的信道中，这种干扰尤为严重，因为不同频率的子载波可能会经历不同的衰落特性。论文通过数学分析，给出了精确的干扰项功率公式，这些公式能够帮助理解误差对信号质量的具体影响，并可以计算出平均信号与干扰比，这是衡量系统性能的重要指标。此外，作者还进一步扩展了分析，考虑了亚采样级别的定时误差，这意味着即使是非常微小的时间偏移也会被纳入考虑，这通常在高速通信或高精度要求的场景中是必要的。通过这些分析，研究揭示了定时误差对OFDM系统性能的非对称效应，即误差在不同方向上的影响可能不一致，这对于优化同步算法和设计抗干扰策略具有指导意义。最后，论文中的仿真结果支持了理论分析，提供了实际应用中的性能评估。这篇工作对于理解OFDM系统在实际环境中的性能限制，以及开发更有效的同步算法以减少同步误差的影响，具有重要的理论和实践价值。

226 IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 54, NO. 2, FEBRUARY 2006

Mathematical Analysis of the Impact of Timing Synchronization

Errors on the Performance of an OFDM System

Yasamin Mostoﬁ, Member, IEEE, and Donald C. Cox, Fellow, IEEE

Abstract—This letter addresses the effect of timing synchro-

nization errors that are introduced by an erroneous detection

of the start of an orthogonal frequency-division multiplexing

(OFDM) symbol.

Such errors degrade the performance of an

OFDM receiver by introducing intercarrier interference (ICI) and

intersymbol interference (ISI). They can occur due to either an

erroneous initial frame synchronization or a change in the power

delay proﬁle of the channel. In this letter, we provide a mathemat-

ical analysis of the effect of timing errors on the performance of

an OFDM receiver in a frequency-selective fading environment.

We ﬁnd exact formulas for the power of interference terms and

the resulting average signal-to-interference ratio. We further

extend the analysis to the subsample level. Our results show the

nonsymmetric effect of timing errors on the performance of an

OFDM system. Finally, simulation results conﬁrm the analysis.

Index Terms—Orthogonal frequency-division multiplexing

(OFDM), signal-to-interference ratio (SIR), timing-synchroniza-

tion errors.

I. INTRODUCTION

RTHOGONAL frequency-division multiplexing

(OFDM) divides the given bandwidth into narrow

subchannels. It handles delay spread by sending low data rates

in parallel on these subchannels [1]. By adding a guard interval

to the beginning of each OFDM symbol, the effect of delay

spread (provided that there is perfect synchronization) would

appear as a multiplication in the frequency domain. Adding

the guard interval will also prevent intersymbol interference

(ISI).

Timing-synchronization errors, however, degrade the

performance of an OFDM receiver by introducing intercarrier

interference (ICI) and ISI. Several methods have been proposed

for timing synchronization in OFDM receivers [2]–[6]. To

evaluate and improve the performance of these methods, a

comprehensive mathematical analysis of the effect of timing

errors and the underlying interference terms is necessary.

Paper approved by R. De Gaudenzi, the Editor for Synchronization and

CDMA of the IEEE Communications Society. Manuscript received July 30,

2003; revised July 27, 2005. This paper was presented in part at the 37th

Asilomar Conference on Signals, Systems, and Computers, Monterey, CA,

November 2003.

Y. Mostoﬁ is with the California Institute of Technology, Pasadena, CA 91125

USA (e-mail: yasi@cds.caltech.edu).

D. C. Cox is with the Department of Electrical Engineering, Stanford Uni-

versity, Stanford, CA 94305 USA (e-mail: dcox@spark.stanford.edu).

Digital Object Identiﬁer 10.1109/TCOMM.2005.861675

Throughout this letter, the term “timing error” would refer to this type of

error.

The analysis presented in this letter is for the case that no equalization tech-

nique has been used to mitigate the introduced ICI and ISI.

The results of this letter can be easily extended to address the effect of such

errors on DMT modems.

Note that intersymbol interference refers to inter-OFDM symbol-interfer-

ence.

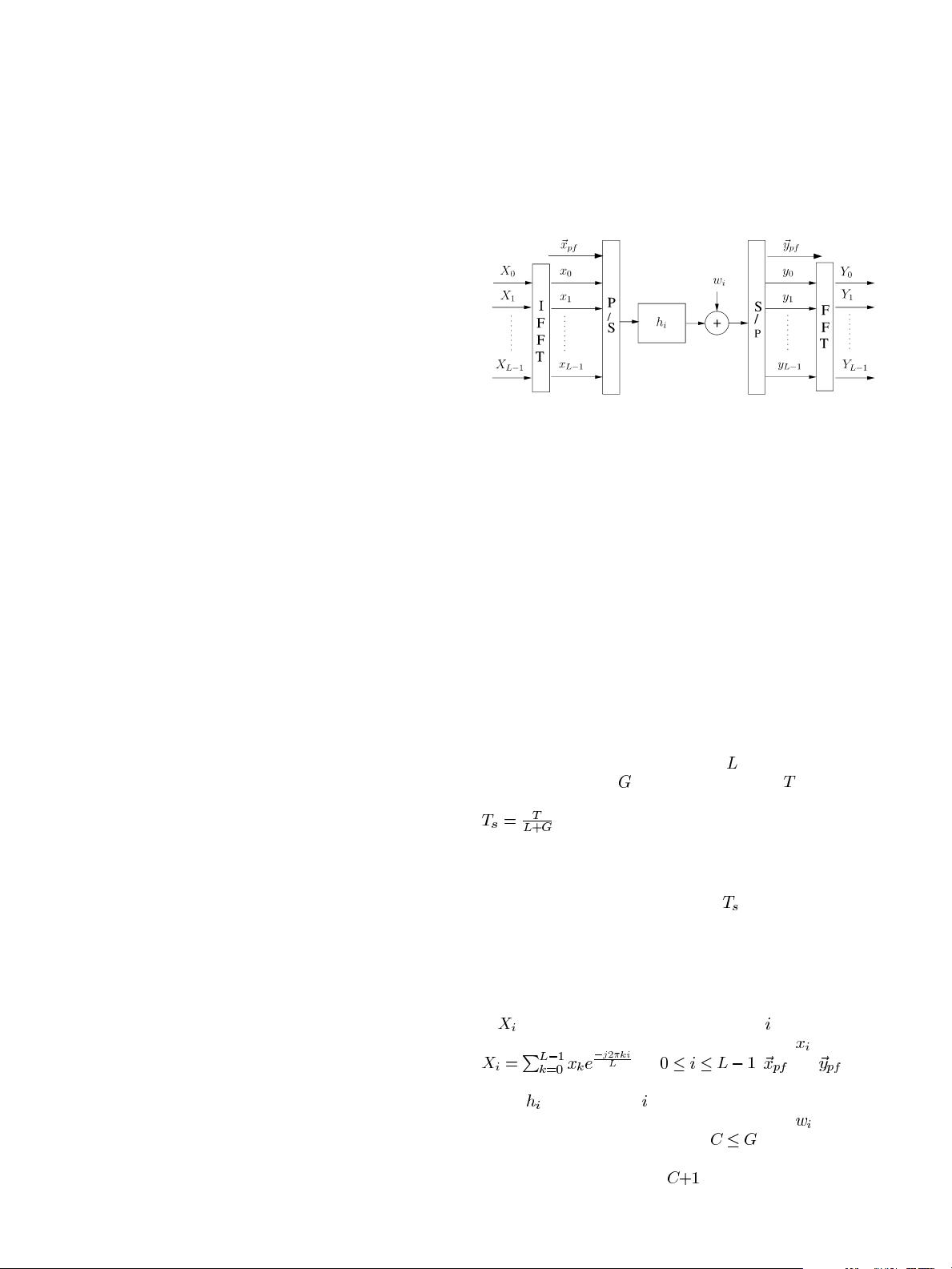
Fig. 1. Discrete baseband equivalent model.

Authors in [5] have provided an approximated formula with lim-

ited applications for the interference caused by timing errors. It

is the goal of this letter to provide an exact mathematical anal-

ysis of the effect of timing errors, which can be a base for eval-

uating the performance of different synchronization methods.

Furthermore, while most of the work on timing synchronization

use sampling-period-level modeling, we also show how to ana-

lyze and evaluate the performance on the subsample level.

II. E

FFECT OF TIMING SYNCHRONIZATION ERRORS

(SAMPLING-PERIOD LEVEL)

Consider an OFDM system, shown in Fig. 1, in which the

available bandwidth is divided into

subchannels, and the

guard interval spans

sampling periods. Let represent the

length of an OFDM symbol (including the guard interval). Then

is the sampling period. In this section, we keep the

analysis on the sampling-period level, which translates to the

following assumptions:

1) no oversampling is done in the receiver;

2) timing error is a multiple of

We relax these conditions in Section III, where we extend the

analysis to include oversampling.

A. System Model

represents the transmitted data in the th frequency sub-

band and is related to the time-domain sequence

as follows:

for . and repre-

sent the transmitted and received cyclic preﬁxes (CPs), respec-

tively.

represents the th channel tap with Rayleigh fading

amplitude and uniformly distributed phase, and

is additive

white Gaussian noise (AWGN). Let

represent the length

of the channel delay spread normalized by the sampling period.

Then the channel would have

taps. In the absence of timing

下载后可阅读完整内容，剩余4页未读，立即下载

小溪水321

粉丝: 1
资源: 10

OFDM系统中定时同步误差影响的数学分析

Mathematical analysis of random noise（随机噪声的数学分析-完整版）

Foundations of Mathematical Analysis

Mathematical Analysis of Algorithms

Mathematical Analysis of Super-Resolution Methodology

Mathematical analysis of stage-based programmable logic controller

Mathematical Analysis

priciples of mathematical analysis 数学分析原理

Principles of Mathematical Analysis, 3rd edition

Principles of mathematical analysis by Walter Rudin

数学分析Rudin Principles of Mathematical Analysis

最新资源