序贯模块法在化工系统工程中的应用与子系统切割策略

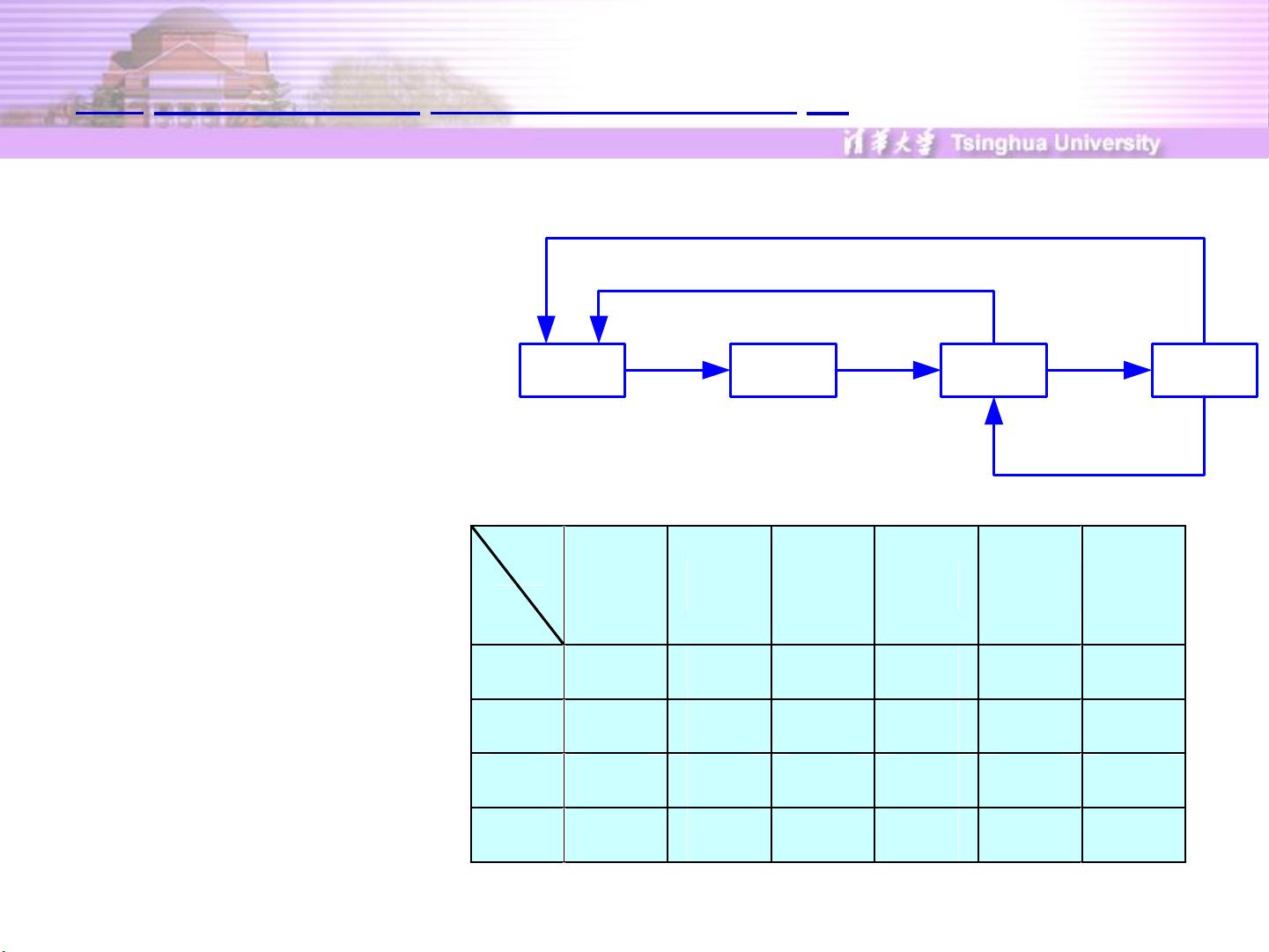
"化工系统工程基础课件 - 序贯模块法-子系统切割.ppt" 在化工系统工程中，序贯模块法是一种重要的系统模拟和优化技术，它主要用于解决复杂的过程系统中的计算问题。该方法的基本思想是将一个大的、包含循环回路的系统分解为多个独立的子系统，然后对这些子系统进行有序求解，最终组合得到整个系统的解决方案。这种方法有助于简化计算过程，提高计算效率，并实现系统的优化。 在序贯模块法中，首先要进行子系统识别，这一步骤涉及到将整个系统划分为多个没有循环回路的子系统，每个子系统具有明确的输入和输出，可以独立计算。接着，对于包含循环回路的子系统，需要进行子系统切割，即选择合适的物流变量作为切割流线，赋予假定值，使得回路中的单元能够顺序求解。切割流线的选择通常有多种方案，但需要根据特定标准来确定最佳方案，如切割流线的数量最少、物流变量总数最少或加权和最小等，以保证求解的效率和精度。 切割回路的一个关键概念是简单回路，它是指在信息流图上，从一个节点出发，沿着流线方向经过不同的节点，最后返回原出发节点的单向环路。简单回路可以用回路矩阵来表示，矩阵中的元素a_ij表示简单回路i是否包含流线j。简单回路必须满足每个单元只经过一次的条件。 为了确定最优切割集，可以设立切割判据，例如最小化切割流线数量、最小化物流变量总数、最小化加权和，以及尽量减少简单回路的切割次数。这些判据有助于在保证求解质量的同时，减少迭代次数，提高计算的收敛速度。 在实际应用中，需要构建回路矩阵来描述系统中的简单回路和流线关系。通过对回路矩阵的分析，可以找出流线与回路的关联，形成流线集合和回路集合，从而帮助确定哪些流线应该被选为切割流线，以覆盖回路矩阵中的所有行和列，实现子系统的有效切割。 通过上述步骤，可以逐步解决化工系统中的复杂计算问题，实现系统的高效模拟和优化。在实际操作中，可能还需要结合其他数学方法和软件工具，如线性规划、非线性规划等，以确保计算的准确性和实用性。对于工程师来说，理解和掌握序贯模块法及其子系统切割策略是优化化工过程设计和操作的关键技能。