探究Kimber-Martin-Ryskin UPDF的积分与微分版本：两种约束与MMHT2014 PDF的实验验证
34 浏览量
更新于2024-09-03
收藏 718KB PDF 举报
本文档标题为《Eur.Phys.J.C (2019) 79:615 - A phenomenological investigation of the integral and differential versions of the Kimber–Martin–Ryskin unintegrated parton distribution functions using two different constraints and the MMHT2014 PDF》。这是一篇发表在《欧洲物理杂志C》上的理论物理学研究文章，作者是N. Olanj和M. Modarres，分别来自伊朗布阿利萨因大学和德黑兰大学的物理系。
研究的核心内容是对 Kimber-Martin-Ryskin (KMR) 不整合部分子分布函数（Unintegrated Parton Distribution Functions, UPDF）的定性探讨。KMR UPDF是量子色动力学(QCD)中用于描述强相互作用下短距离结构的重要工具，特别是在高能物理实验中，如深inelastic散射和重离子碰撞中，它们用于预测粒子的生成和衰变。
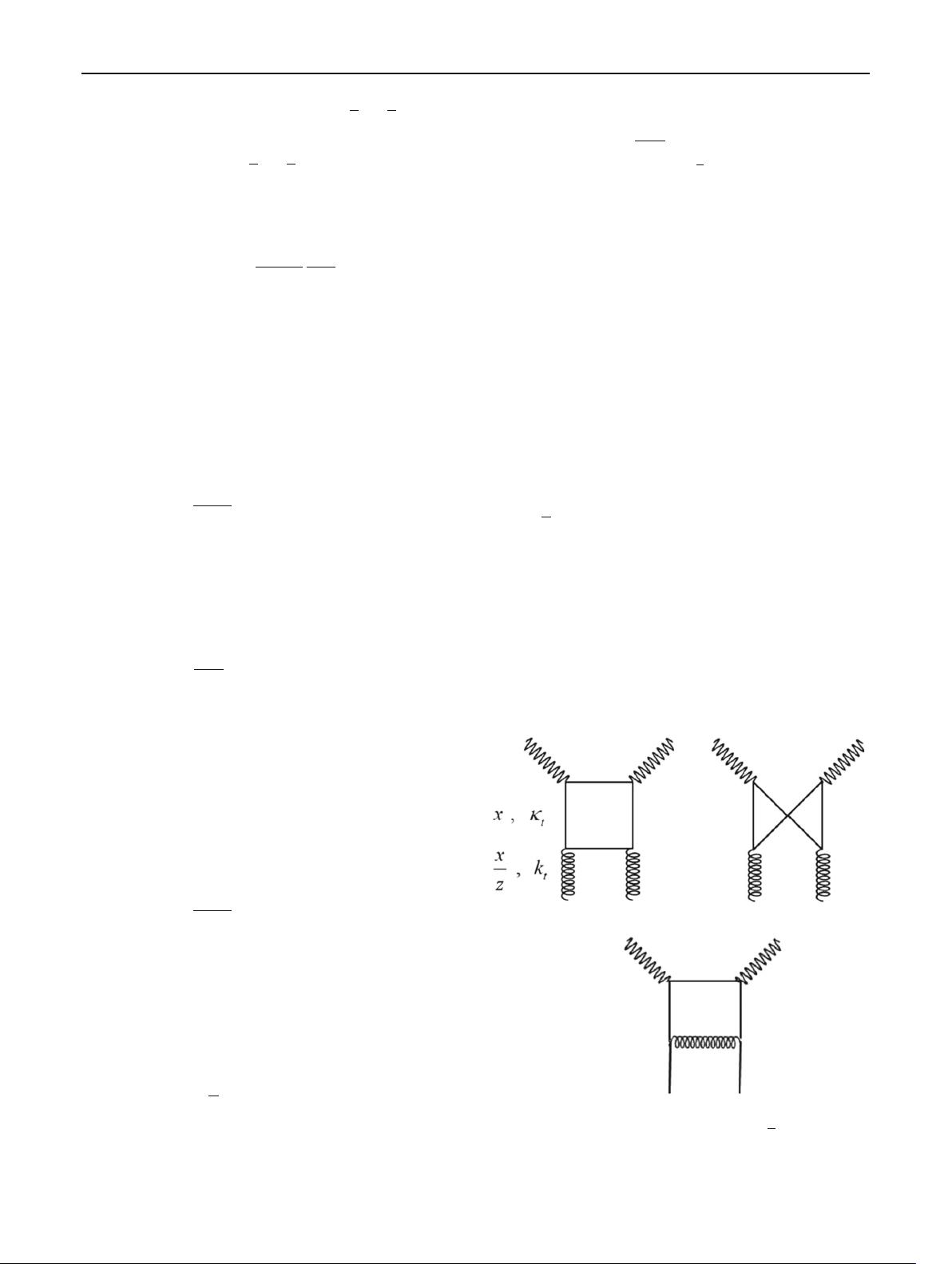
在这篇文章中，作者回顾了之前关于KMR UPDF与实验数据，特别是关于质子（longitudinal）结构函数（PSF, PLSF）的兼容性研究。他们特别关注的是KMR的差分形式以及与角（或强）秩序约束（Angular Ordering, AO 或 Strong Ordering, SO）相结合的情况。这些约束在计算过程中对UPDF的行为有着显著影响。
作者指出，Golec-Biernat和Stasto（GBS）最近的研究揭示了一个问题：当采用普通部分子分布函数（PDF）作为输入，并结合KMR的差分版本以及AO或SO约束时，可能导致出现负的、不连续的UPDF。这种结果显然与理论预期和实验数据的连续性相违背，因此引发了深入的理论探讨。
文章的主要贡献在于通过两种不同的约束条件对KMR UPDF进行了系统分析，并且使用了MMHT2014年版的PDF作为输入，目的是为了理解这种不连续性的来源，以及可能的修正策略。作者可能会提出改进KMR框架的方法，或者探索其他可能的原因，比如数据处理误差、模型假设或计算方法的局限性。
这篇论文对于理解KMR UPDF的理论发展、如何处理其在实际应用中的问题以及如何更好地将其与实验数据融合具有重要意义，对于那些研究高能物理和QCD动力学的科研人员来说，它是了解UPDF最新进展的宝贵资源。
Eur. Phys. J. C (2019) 79 :615 Page 3 of 11 615
×
1−
x
dz
q
P
gq
(z)
x
z
q
x
z
, k
t
2
+P
gg
(z)
x
z
g
x
z
, k
t
2
, (2)
respectively, while survival probability factor T
a
is evaluated
from:
T
a
(k
t
, Q) = exp
−
Q
2
k
2
t
α
s
(k
t
2
)
2π
dk
t
2
k
t
2
×
a
1−
0
dz
P
a
a
(z
)
. (3)
In this approach only at the last step of the evolution does the
dependence on the second scale, Q, get introduced into the
UPDF.
2. Differential form:
The differential form of the KMR approach generates UPDF
by using the derivation of the integrated PDF, as follows:
f
a
(x, k
2
t
, Q
2
) =
∂
∂lnλ
2
[a(x,λ
2
)T
a
(λ, Q)]
λ=k
t
, (4)
where T
a
obtained from Eq. (3).
The required PDF are provided as the input, using the
libraries MRST99 [15], MSTW2008 [16] and MMHT2014
[24], where the calculation of the single-scaled functions are
carried out using the deep-inelastic scattering (DIS) data on
the F
2
(x, Q
2
) structure function of the proton. The cutoff,
= 1 − z
max
=
k
t
Q+k
t
, is determined by imposing the AOC
on the last step of the evolutionary, to prevent the z = 1sin-
gularities in the splitting functions, which arise from the soft
gluon emission. Also, T
a
(k
t
, Q) is considered to be unity for
k
t
> Q. This constraint and its interpretation in terms of the
angular ordering condition gives the integral form of the KMR
approach a smooth behavior over the small-x region, which is
generally governed by the Balitsky–Fadin–Kuraev–Lipatov
(BFKL) evolution equation [27,28]. Notice that considering
T
a
(k
t
, Q) = 1fork
t
> Q, the differential form of the KMR
approach is converted to the following equation:
f
a
(x, k
2
t
, Q
2
) =
∂
∂lnλ
2
[a(x,λ
2
)]
λ=k
t
. (5)
As we stated above to prevent the z = 1 singularities in the
splitting functions, which arise from the soft gluon emission,
two types of cutoffs, , were introduced, such that in the
Eqs. (1), (2) and (3), x to be less than (1 − ):
1. The strong ordering constraint (SOC) on the transverse
momentum of the real parton emission in the DGLAP
evolution: =
k
t
Q
. In this case, the nonzero values of the
UDPF are given for k
t
≤ Q(1 − x) and therefore, we
always have k
t
< Q and T
a
< 1.
2. The angular ordering constraint (AOC) that we explained
above, which is the key dynamical property of the CCFM
formalism: =
k
t
Q+k
t
, so the nonzero values of the
UDPF are given for k
t
≤ Q(
1
x
− 1) and T
a
is considered
to be unity for k
t
> Q (see GBS).
3 A glimpse of F
2
(x, Q
2
) and F
L
(x, Q
2
) in the
k
t
-factorization approach
Here we briefly describe the different steps for calculations
of the proton structure functions (F
2
(x, Q
2
)) and the pro-
ton longitudinal structure functions (F
L
(x, Q
2
))inthek
t
-
factorization approach. The k
t
-factorization approach was
discussed in several works, for example the references [7,29–
31]. Since the gluons in the proton can only contribute
to structure functions through the intermediate quark, so
one should calculate the proton structure functions in the
k
t
-factorization approach by using the gluons and quarks
UPDF.Theunintegrated gluons and quarks contributions
to F
2
(x, Q
2
) and F
L
(x, Q
2
) come from the subprocess
g → q
q and q → qg, respectively (see the figure 6 of
the reference [32]). The relevant diagrams by considering a
physical gauge for the gluon, i.e., A
μ
q
μ
= 0 (q
= q + xp),
are those shown in the Fig. 1 (the figure 7 of the reference
[13]).
Fig. 1 The diagrams contributing in the calculation of the structure
functions F
2
(x , Q
2
), which comes from the g → qq and q → qg
123
剩余10页未读，继续阅读
2018-12-13 上传
2024-04-12 上传
2024-11-12 上传
2024-11-12 上传
2024-11-12 上传
weixin_38502292
- 粉丝: 5
- 资源: 965
我的内容管理
展开
最新资源
- 前端协作项目：发布猜图游戏功能与待修复事项
- Spring框架REST服务开发实践指南
- ALU课设实现基础与高级运算功能
- 深入了解STK：C++音频信号处理综合工具套件
- 华中科技大学电信学院软件无线电实验资料汇总
- CGSN数据解析与集成验证工具集：Python和Shell脚本
- Java实现的远程视频会议系统开发教程
- Change-OEM: 用Java修改Windows OEM信息与Logo
- cmnd：文本到远程API的桥接平台开发
- 解决BIOS刷写错误28：PRR.exe的应用与效果
- 深度学习对抗攻击库：adversarial_robustness_toolbox 1.10.0
- Win7系统CP2102驱动下载与安装指南
- 深入理解Java中的函数式编程技巧
- GY-906 MLX90614ESF传感器模块温度采集应用资料
- Adversarial Robustness Toolbox 1.15.1 工具包安装教程
- GNU Radio的供应商中立SDR开发包：gr-sdr介绍
