MATLAB多元非线性回归实战指南
版权申诉
"matlab多元非线性回归教程"
这篇文档是关于在MATLAB中进行多元非线性回归分析的教程。非线性回归是一种统计方法,用于拟合数据到一个非线性的函数模型,这对于理解和预测复杂关系非常有用。在MATLAB中,有几种方法可以实现这一目标,包括`polyfit`、`regress`和`nlinfit`命令。
1. `polyfit`函数:主要用于一元多项式拟合,它可以将数据拟合到一元幂函数模型。例如,如果你知道数据可能遵循某种多项式规律,你可以用`polyfit(x,y,n)`来拟合x和y数据,其中n是多项式的阶数。
2. `regress`函数:适用于多元线性回归,可以处理多个自变量对因变量的影响。例如,如果模型形式为`y = β0 + β1*x1 + β2*x2 + ... + βp*xp + e`,其中y是因变量,x1到xp是自变量,β0到βp是待求的系数,e是误差项,那么`regress(y,x)`可以求解这些系数。注意,使用此函数时,x矩阵应包含一个额外的全1列代表常数项,且y必须是列向量。
3. `nlinfit`函数:这是最通用的非线性回归工具,可以拟合任何用户定义的非线性函数。只需提供函数的数学形式('fun')和初始系数估计(beta0),`nlinfit(x,y,'fun',beta0)`就能计算出最佳拟合参数。这个命令特别灵活,适用于各种复杂的非线性模型。
回归分析的基本步骤包括:
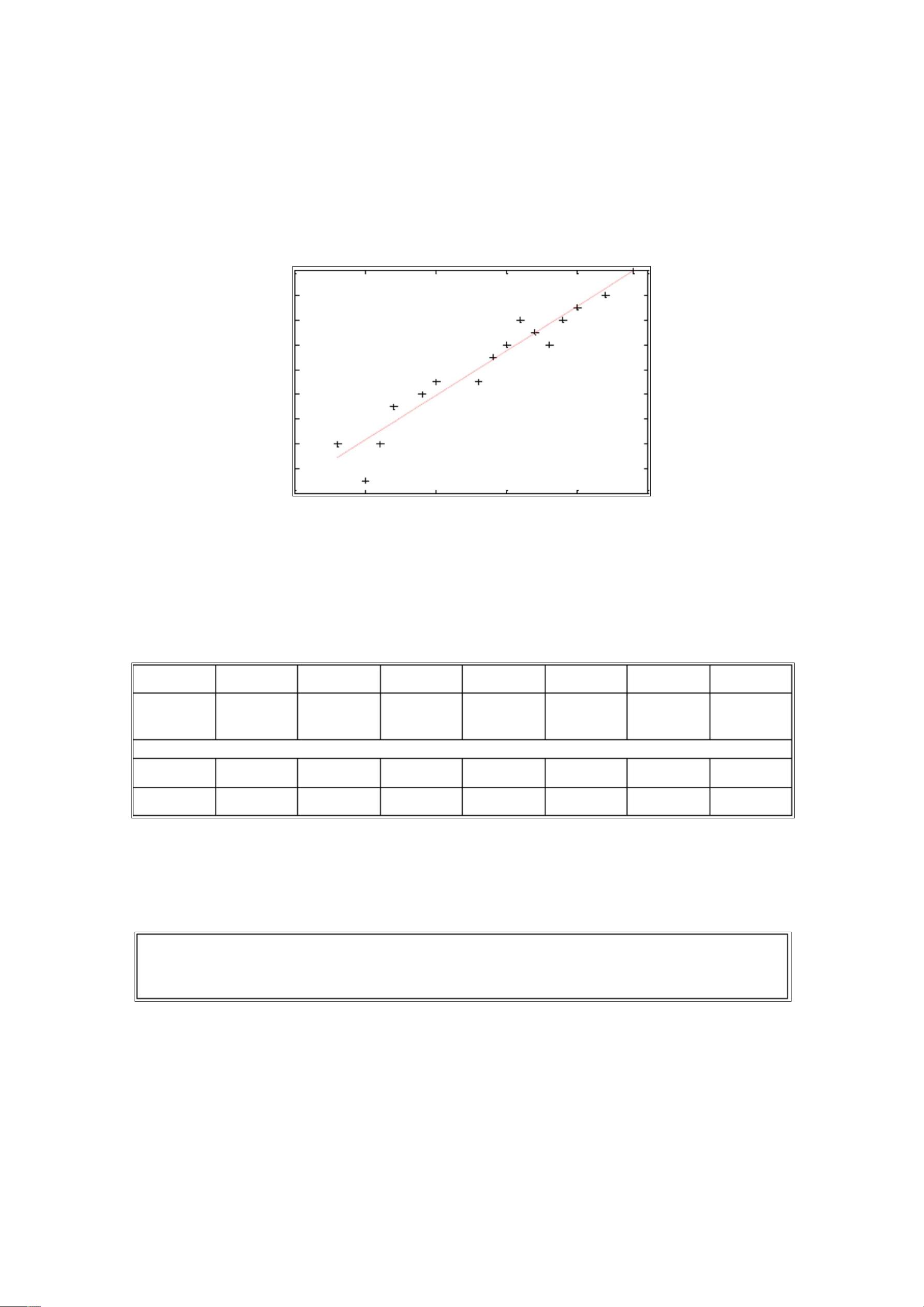
- 观察数据图,选择合适的函数类型。
- 写出函数的一般形式,包含待定系数。
- 使用适当的MATLAB命令求解这些系数。
对于多元线性回归模型,数据表示为`y = β0 + β1*x1 + β2*x2 + ... + βp*xp + e`,其中x是n×p矩阵,每一行代表一个观测值,p是自变量的数量,y是n×1向量,表示因变量的观测值。通过`regress`函数,我们可以得到系数估计值(b),其间隔估计(bint),残差(r)及其置信区间(rint),以及统计量(stats),包括相关系数等,用于评估模型的适合度。
在进行多元非线性回归时,`nlinfit`尤其重要,因为它允许用户自定义函数形式,从而适应各种非线性关系。不过,选择合适的模型和初始化参数(beta0)对于获得准确的拟合结果至关重要。
MATLAB提供了强大的工具来处理多元非线性回归问题,无论是简单的多项式拟合,还是复杂的自定义函数模型,都能有效应对。在实际应用中,理解每个函数的工作原理,结合数据特性,选择合适的回归方法,以及对结果进行合理解释,都是进行有效数据分析的关键。
2022-06-30 上传
2022-06-23 上传
2022-10-30 上传
2022-06-23 上传
2022-06-23 上传
2022-06-23 上传
apple_51426592
- 粉丝: 9841
- 资源: 9652
最新资源
- 集成测试工作流程指南.pdf
- 《Core Java-VOLUME I-FUNDAMENTALS EIGHTH EDITION》
- Ospf协议讲解及配置
- java的JNI跨平台技术
- 关于SQL注入的资料-2
- 卫星测高--GPS测高的原理
- 如何使用C语言来编写 MSP430的高质量代码
- linux下建立自动编译环境.pdf
- 8259a单片机程序
- CImg库参考手册.pdf
- 网络工程师考试2008年下半年下午试题解析
- 使用+Visual+Studio+[1].NET+创建+BREW_+应用程序.pdf
- JAVA面试题解惑系列
- Struts In Action PDF 完整中文版
- 武汉大学选修课Matlab作业
- PICC编程简介PIC单片机C语言编程入门