离散数学深入讲解：函数的定义与递归

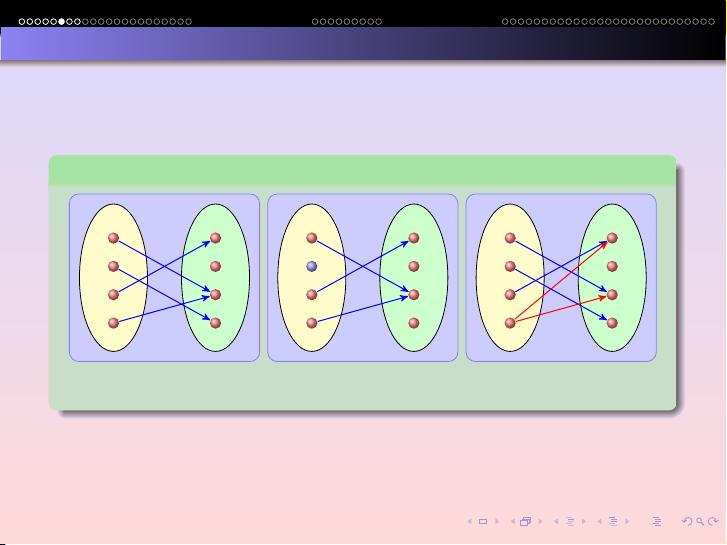
"离散数学中的函数教学，涵盖尾递归、映射、单射、满射等核心概念" 在离散数学中，函数是一种重要的数学工具，用于描述两个集合之间的关系，其中每个元素在源集合中都有唯一确定的对应元素在目标集合中。本教学资料深入探讨了函数的各种特性，包括基本概念、分解和递归定义。 1. 函数的基本概念 函数定义为一个规则，它将一个集合（定义域）的每个元素映射到另一个集合（值域）的一个元素。函数用f表示，通常写作f: A → B，其中A是定义域，B是值域。每个a ∈ A都有一个对应的值f(a) ∈ B。函数的关键特性是其一对一性，即对于不同的a ∈ A，f(a)也是不同的。 2. 函数的象和逆象 - 函数的象是指所有在函数作用下有映射的元素形成的集合，记作f(A)。 - 函数的逆象是对于某个特定值y ∈ B，所有映射到y的元素a ∈ A组成的集合，记作f^(-1)(y)。如果函数是满射，那么对于B中的每个元素都有至少一个来自A的元素映射到它。 3. 函数的合成 函数的合成允许我们将两个或多个函数组合成一个新的函数。给定两个函数f: A → B和g: B → C，它们的合成g ∘ f: A → C是一个新的函数，其中(g ∘ f)(a) = g(f(a))。 4. 单射、满射和双射 - 单射（Injective）：函数f使得对所有a, b ∈ A，若f(a) = f(b)，则a = b。这意味着每个元素在值域中都有唯一的映射。 - 满射（Surjective）：函数f使得B的每一个元素都是f(A)中的元素，即对于所有b ∈ B，存在a ∈ A，使得f(a) = b。 - 双射（Bijective）：既是单射又是满射的函数，它提供了一个集合到另一个集合的完美映射，且存在唯一逆函数。 5. 函数的分解 函数的分解是将一个复杂的函数表示为更简单的函数组合。例如，可以将一个函数分解为若干个单射和满射的组合，以便更好地理解和操作它。 6. 函数的递归定义 递归定义是通过使用自身来定义函数的方法。在自然数集合上，递归函数如欧几里得算法（用于计算最大公约数）展示了如何通过已知的函数结果来定义新的结果。尾递归是递归的一种特殊情况，它在函数返回时直接调用自身，而不需要进一步的计算。此外，还有如List集合上的递归定义函数，以及更复杂的函数，如Ackerman函数，这些函数的定义涉及自身的多次应用。高阶函数允许我们传递函数作为参数或返回函数作为结果，这在递归定义中尤其有用。 通过深入学习这些概念，学生可以更好地理解离散数学中的函数理论，为计算机科学中的算法设计、数据结构和其他领域打下坚实基础。