主成分分析详解：步骤与特征值计算

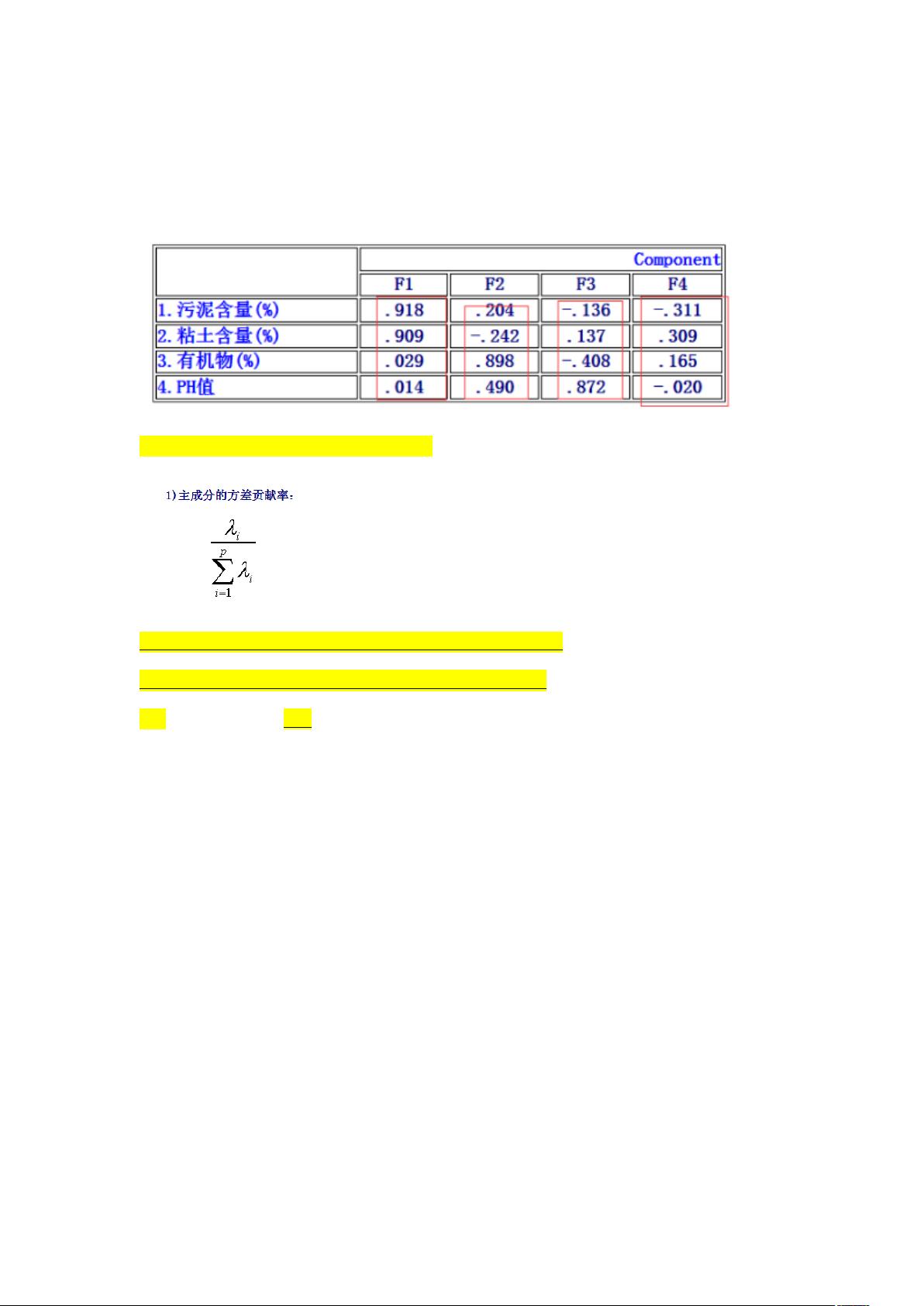
主成分分析是一种统计方法，用于将多个可能相关的变量转化为少数几个新的变量，这些新变量称为主成分，它们是原始变量的线性组合，并且彼此间尽可能不相关。这种方法常用于数据分析中的降维，能帮助简化数据结构，减少分析复杂性。 在进行主成分分析时，遵循以下步骤： 1. **选择变量**：首先，根据研究目标选择相关的变量，这些变量通常应具有一定的变异性和相互关联性。 2. **计算相关系数矩阵**：通过计算变量之间的皮尔逊相关系数，构建相关系数矩阵。这个矩阵反映了所有变量之间的相互关系，是主成分分析的基础。 3. **求解特征值和特征向量**：对相关系数矩阵进行特征值分解，得到各个特征值和对应的特征向量。特征值代表了矩阵的方差信息，而特征向量则表示了主成分的方向。特征值越大，对应的主成分解释的数据变异程度越高。 4. **排序特征值和特征向量**：特征值按照大小进行排序，一般从大到小。总和等于原始变量的个数。特征向量则与对应的特征值一起考虑，它们共同决定了主成分的构成。 5. **计算累积贡献率**：将特征值除以其总和，得到单个特征值的贡献率，累积贡献率是所有特征值贡献率的累加。通常，为了保证信息的保留，会选择累积贡献率达到85%或以上的一组主成分。 6. **确定主成分个数**：根据累积贡献率和研究需求，决定提取的主成分数量。有两种常见方法： - 基于特征值：通常选择特征值大于1的主成分，因为一个特征值大于1意味着它解释的方差大于原始变量的一个平均方差。 - 固定数量的因子：用户可以指定提取的主成分个数，通常是介于1到原始变量个数之间的一个整数。 在实际操作中，如使用SPSS等统计软件，用户可以根据这两种方法设定阈值，以确定提取的主成分。完成这些步骤后，就可以将原始数据投影到由提取出的主成分构成的新空间中，从而实现数据的降维和简化分析。 通过主成分分析，我们可以更有效地处理高维数据，减少噪声，同时保持数据的主要信息，这对于数据分析、模型建立以及数据可视化等方面都具有重要意义。