数值分析与插值：从拉格朗日到三次样条

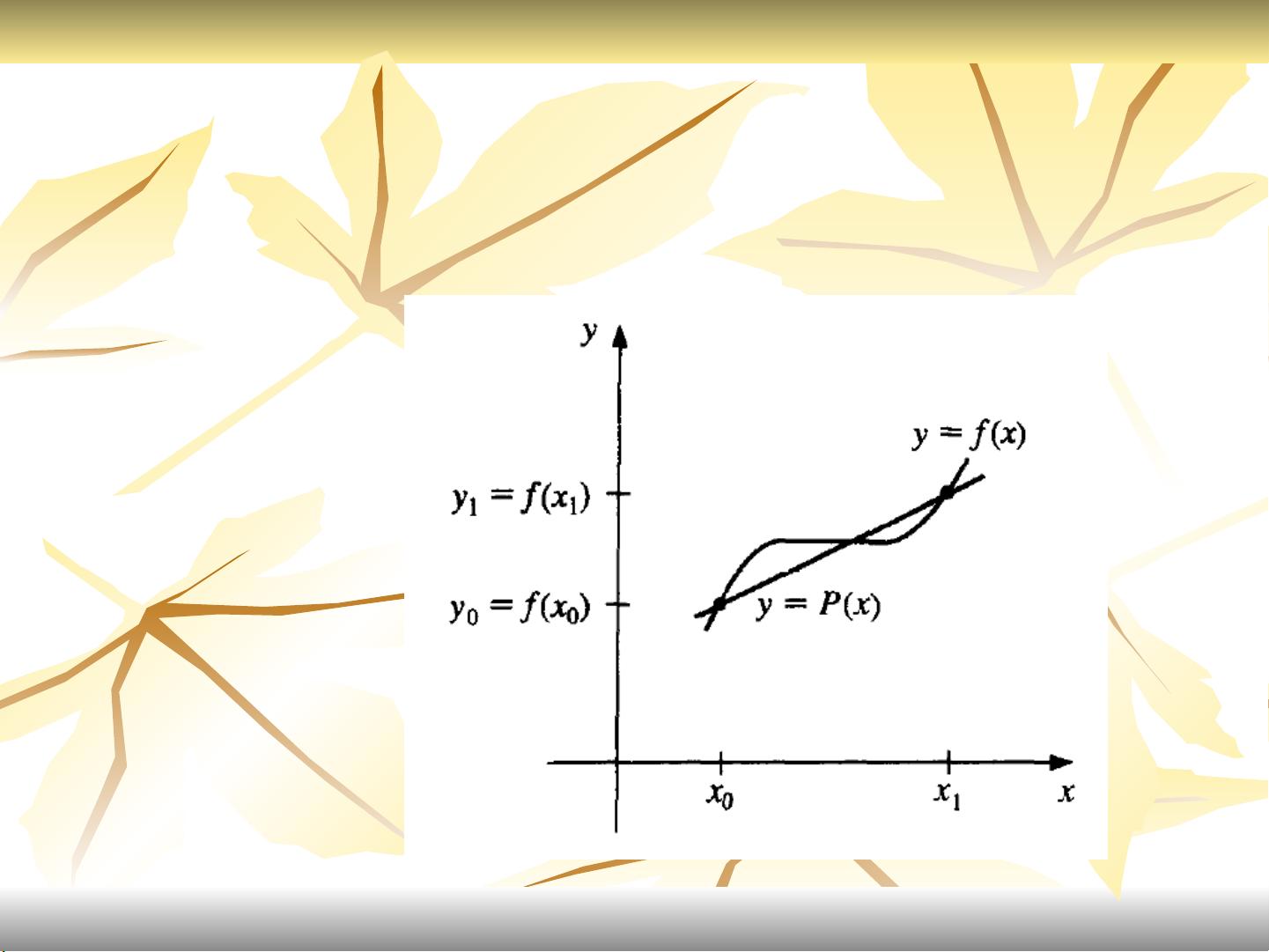
"该资源是一份关于插值的数值分析课件，包含了多项式近似的基本概念和方法，如拉格朗日多项式、牛顿除差法、哈密顿内插以及三样条内插。课件还涉及到泰勒近似、Weierstrass近似定理以及误差分析，并提供了C语言实现样条插值的伪代码。" 在数值分析领域，插值是一种重要的数学技术，用于构建一个多项式函数，这个函数在给定的一系列数据点上精确匹配这些点的值。课件中详细介绍了以下知识点： 1. **引言**：这部分通常会阐述插值的目的，比如通过多项式近似复杂函数或数据，以及泰勒近似和Weierstrass近似定理的基本概念。泰勒近似通过求函数在某一点的导数构建泰勒级数来逼近原函数，而Weierstrass定理指出，任何连续函数都可以被无限次可微的多项式序列以任意精度逼近。 2. **拉格朗日多项式**：这是一种基本的插值方法，通过构造一个多项式，使其在每个给定点上的值都与函数f在该点的值相等。课件中提到了误差分析和内维迭代插值法（Neville's Iterated Interpolation），后者是通过迭代过程逐步构造拉格朗日插值多项式的高效算法。 3. **牛顿除差法**：这种方法基于牛顿前向和后向微分公式，通过差商来近似函数的导数。课件可能包括了如何使用牛顿除差法计算插值多项式，并可能涉及斯特灵公式，这是一个在计算组合数时非常有用的近似公式。 4. **哈密顿内插与三样条内插**：哈密顿内插是将多个线性插值段连接起来以形成光滑曲线的方法，而三样条内插则是哈密顿内插的一种特殊情况，通常用于数据平滑和曲线拟合，特别是在处理连续但不光滑的数据时。 5. **伪代码与C语言实现**：课件提供的伪代码可以帮助理解算法的逻辑流程，而C语言的实现样例则可以让学生实际操作并理解这些插值方法在编程中的应用。 这些内容对学习数值分析和插值技术的学生来说极具价值，不仅提供了理论基础，还有实践应用的示例，有助于提高理解和应用能力。