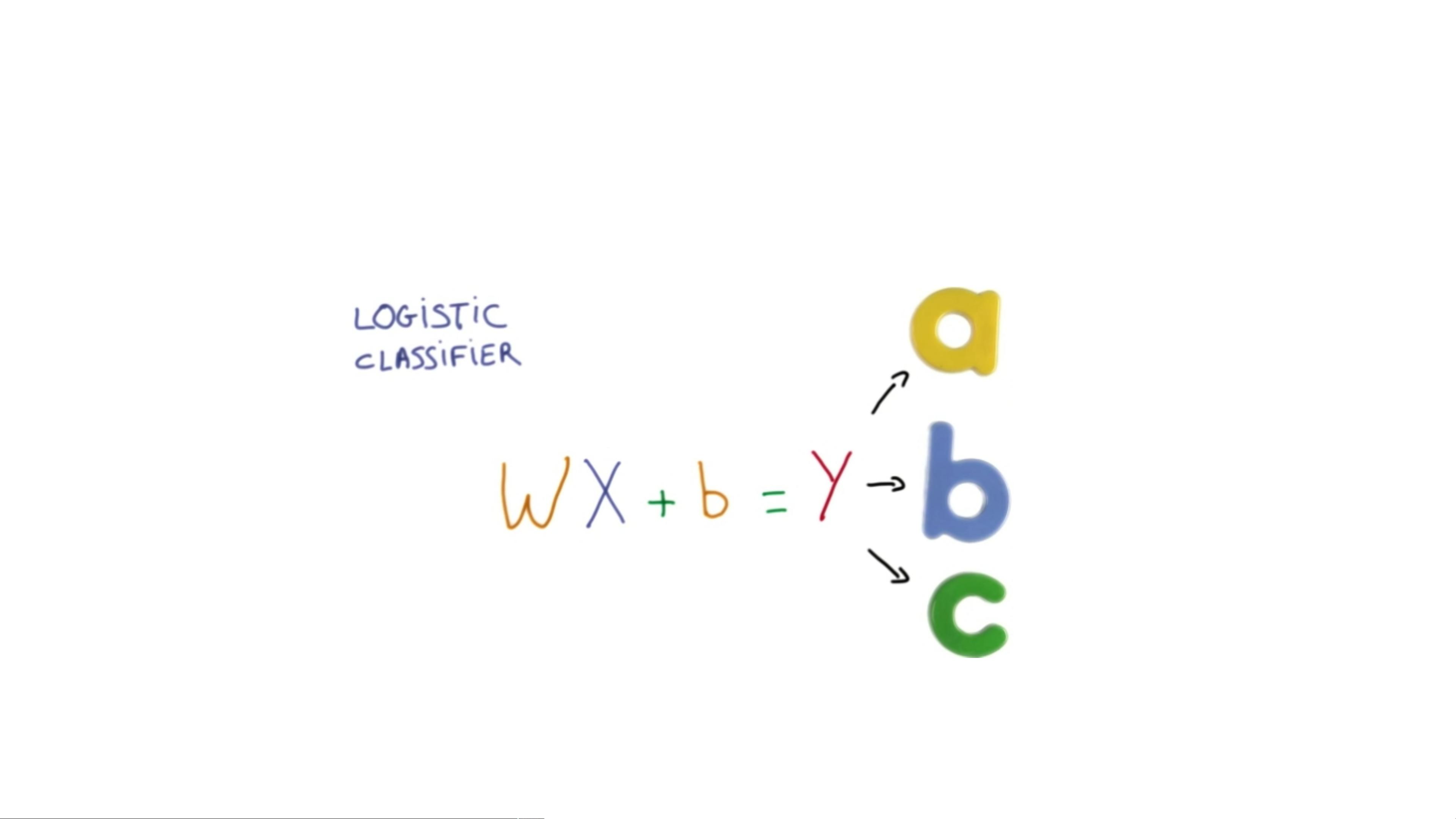深度学习基础：线性回归与softmax分类

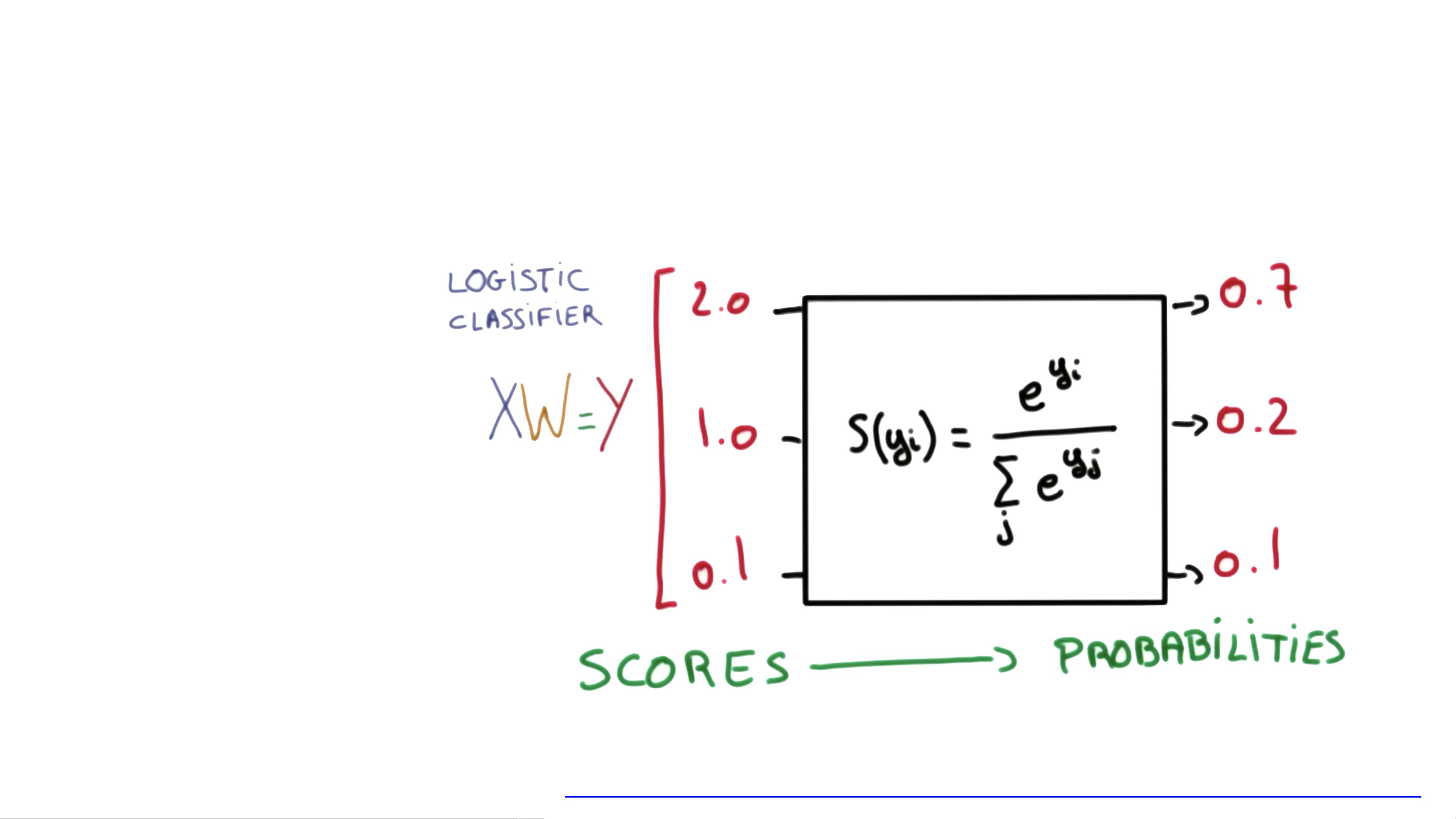
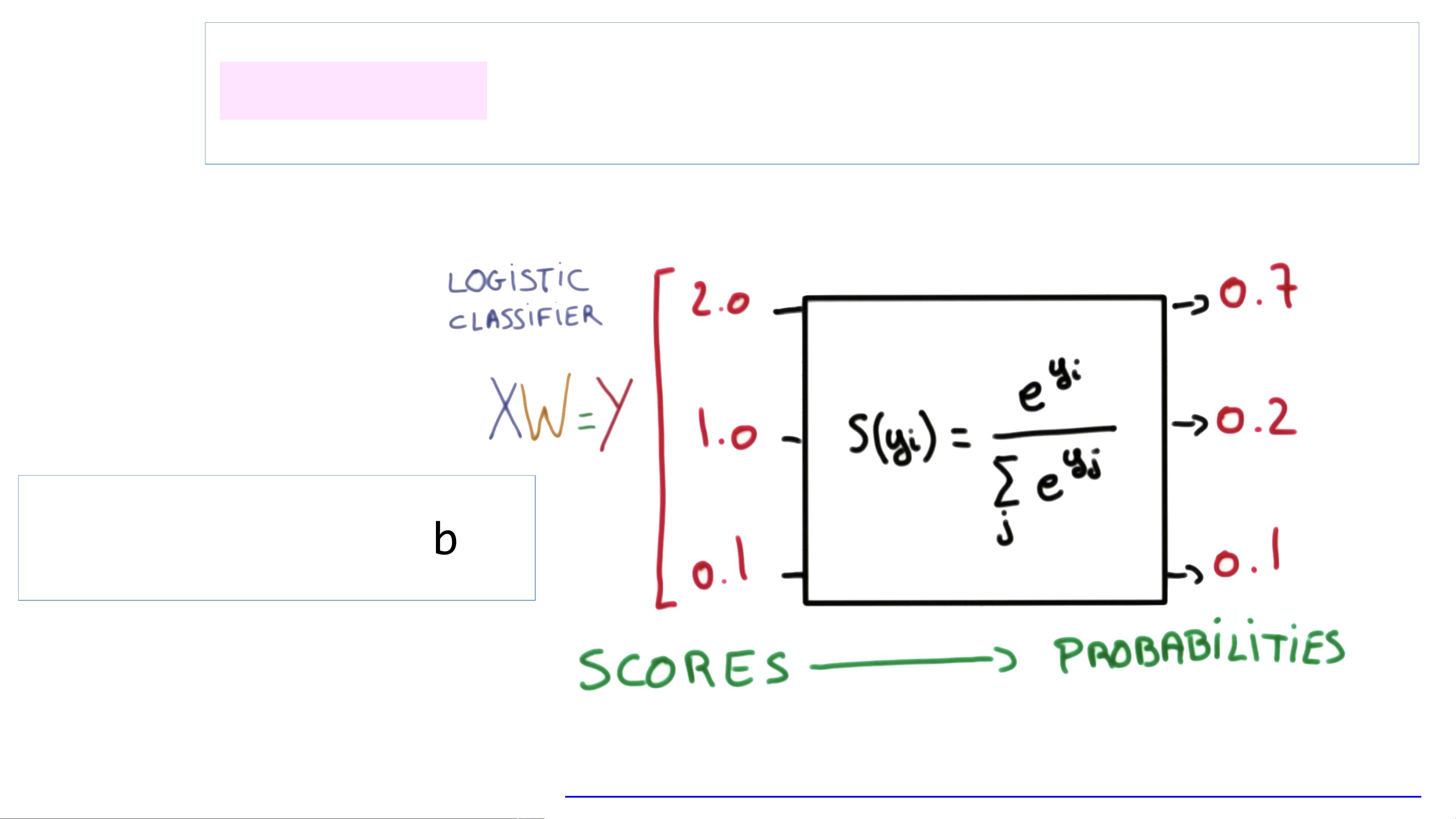
在TF-UST-DAY1.5的PPT中，主要讨论了深度神经网络（Deep Neural Networks）中的基础概念，特别是与机器学习相关的算法。课程首先回顾了机器学习的基本原理，包括线性回归（Linear Regression）和逻辑回归（Logistic Regression）用于二分类问题。逻辑回归的决策边界是通过sigmoid函数实现的，它将线性函数的结果映射到0到1之间，用于预测概率。 接着，课程引入了softmax分类（Softmax Classification），这是一种多分类方法，当有多个可能的类别时，softmax函数被用来将输出转换为每个类别的概率分布。它将线性组合的结果通过softmax函数标准化，确保所有输出之和为1。其数学表达式为：\( hypothesis = \frac{e^{(tf.matmul(X, W) + b)}}{\sum_{j=1}^{n} e^{(tf.matmul(X, W_j) + b_j)}} \)，其中\( X \)是输入特征，\( W \)是权重矩阵，\( b \)是偏置项，\( n \)是类别数量。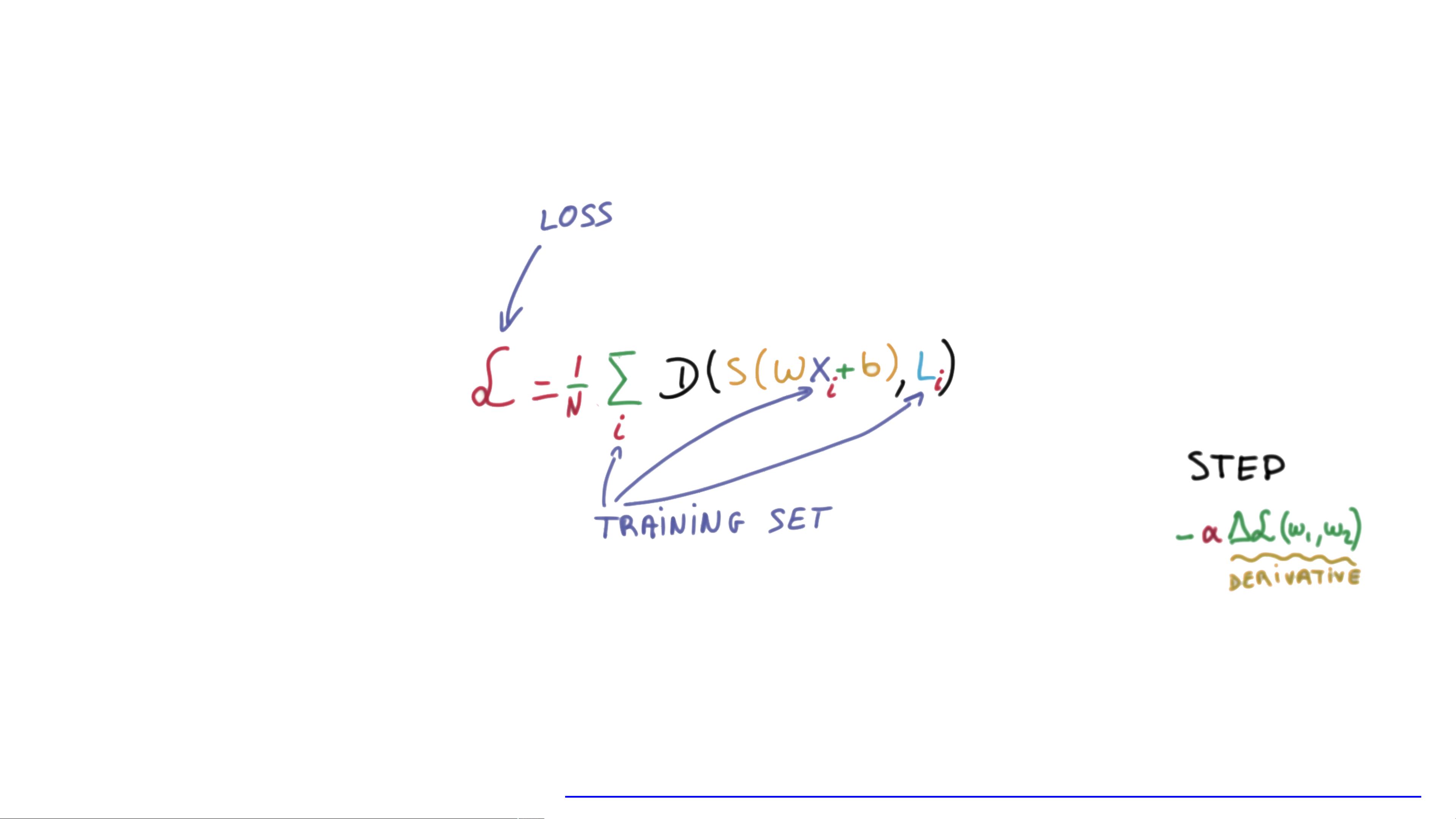 成本函数（Cost Function）的选择对于优化模型至关重要。在这里，主要讲解了交叉熵损失函数（Cross-Entropy Cost/Loss），它是 softmax 函数常用于多分类问题中的性能度量。交叉熵的公式为： \[ cost = -\frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{n} Y_{ij} \log(hypothesis_{ij}) \] 其中，\( m \)是样本数量，\( Y \)是真实的类别标签（one-hot编码），\( hypothesis \)是模型预测的概率向量。这个函数鼓励模型对正确的类别给出更高的预测概率，并对错误的类别给出较低的概率。 课程通过展示不同权重值\( W \)下的成本曲线，直观地解释了如何通过最小化成本函数来优化模型参数，特别是在线性和非线性决策边界情况下。最后，演示了如何在TensorFlow（TF）中使用`tf.nn.softmax`和`tf.reduce_mean`以及`tf.reduce_sum`函数来实现softmax分类和计算交叉熵成本。 TF-UST-DAY1.5的内容涵盖了深度学习的基础构建块，从线性模型到非线性模型的转换，以及关键的优化方法，强调了在实际应用中选择合适成本函数的重要性。这门课程对于理解深度学习的实践操作和理论基础非常有帮助。