数据结构复习关键点：队列、算法复杂度与图的遍历

"福建工程学院的数据结构复习题涵盖了循环队列、时间复杂度、栈的操作、二叉树遍历、有向图的拓扑排序、数组的存储布局、图的深度优先遍历以及最小生成树等核心概念。" 1. 循环队列：循环队列是一种线性数据结构，其特点是队列的最后一个元素后面紧接着队列的第一个元素，形成一个循环。题目中提到的队列长度为20，front=15，rear=5，表示队列中有10个元素（(rear - front + 队列长度) % 队列长度 = (5 - 15 + 20) % 20 = 10）。 2. 时间复杂度分析：这段代码包含两个嵌套循环，分别以i和j为变量，两个循环都是从1到n，因此整个代码块的时间复杂度为O(n^2)，因为对于每一对i和j，都要执行一次a[i][j]的赋值和打印操作。 3. 栈的操作：栈是一种后进先出（LIFO）的数据结构。题目描述了一种不允许连续3次退栈的限制，选项D（afedcb）违反了这一规则，因为在e出栈后，不能立即对f进行退栈，所以这不是可能的退栈顺序。 4. 二叉树遍历：给定前序遍历（ABDEGCFH）和中序遍历（DBGEACHF），可以推导出后序遍历（DGEBHFCA）。前序遍历中第一个元素A是根节点，中序遍历中A的左侧是左子树，右侧是右子树。根据这些信息，可以构建二叉树并进行后序遍历。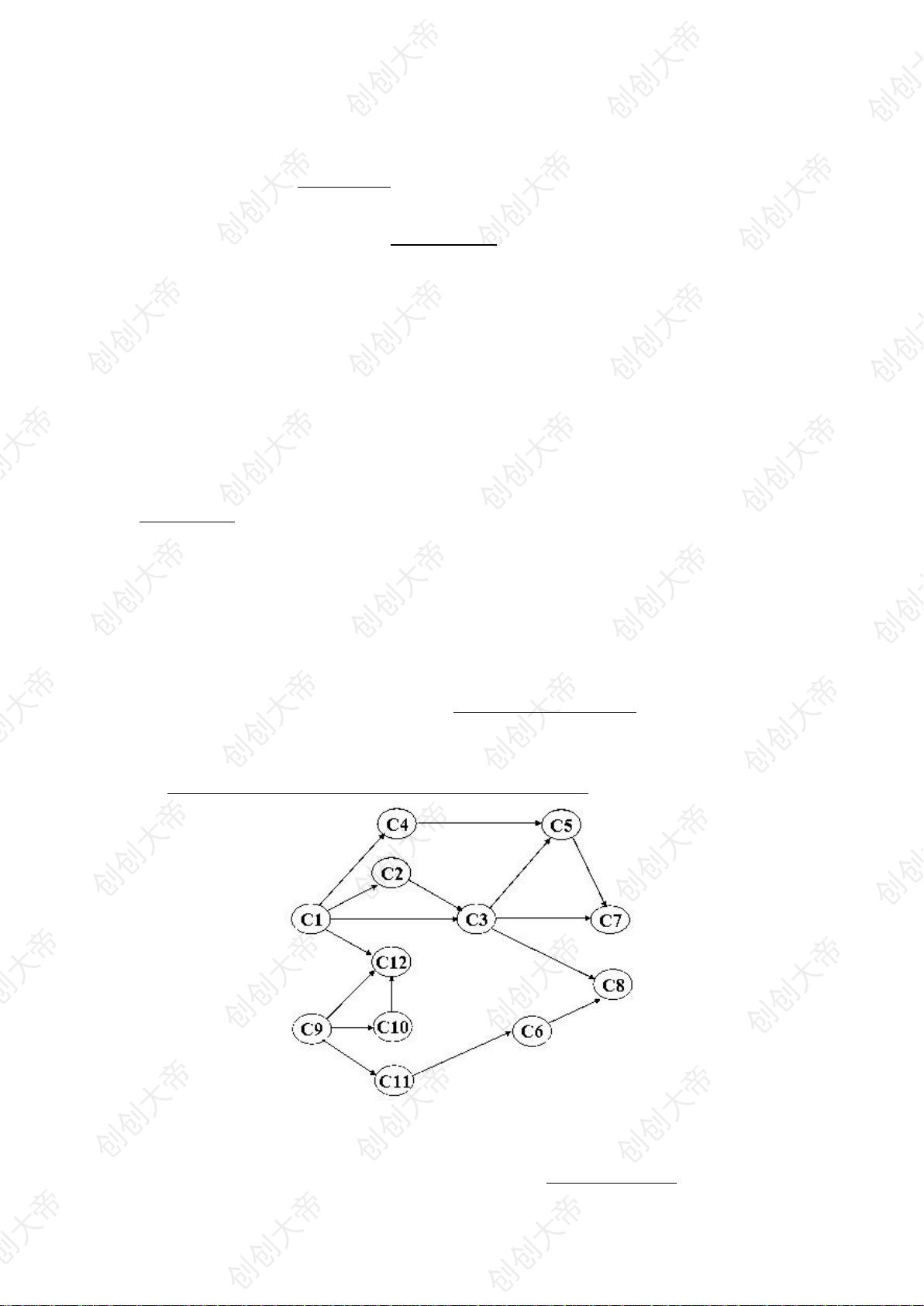 5. 有向图的拓扑排序：拓扑排序是对有向无环图（DAG）的顶点的一种线性排序，使得对于每条有向边(u, v)，u都在v之前。给定的有向图的合法拓扑排序序列为C1-C2-C3-C4-C5-C7-C9-C10-C11-C6-C12-C8，这表明没有环，并且节点按依赖关系正确排序。 6. 数组存储：在行优先存储的二维数组中，A[2,2]的地址可以通过数组基地址加上行索引乘以列数再加上列索引来计算，即10 + (2 - 1) * 3 * 2 + (2 - 1) * 2 = 18。 7. 图的深度优先遍历：深度优先遍历（DFS）按照“深度”优先的原则访问图的节点。题目给出了一个图的DFS序列，它表明了节点的访问顺序。 8. 最小生成树：最小生成树（MST）是无向图中边的一个子集，连接所有节点且总权重最小。题目要求画出给定无向带权图的最小生成树并计算其权值，这是Kruskal或Prim算法的应用。 总结来说，这份复习题涵盖了数据结构中的关键概念，包括基本操作（如循环队列、栈）、复杂度分析、二叉树遍历、图的处理（拓扑排序、最小生成树）以及数组的存储布局，这些都是理解和掌握数据结构课程的重要组成部分。