梯度下降算法解析及其应用

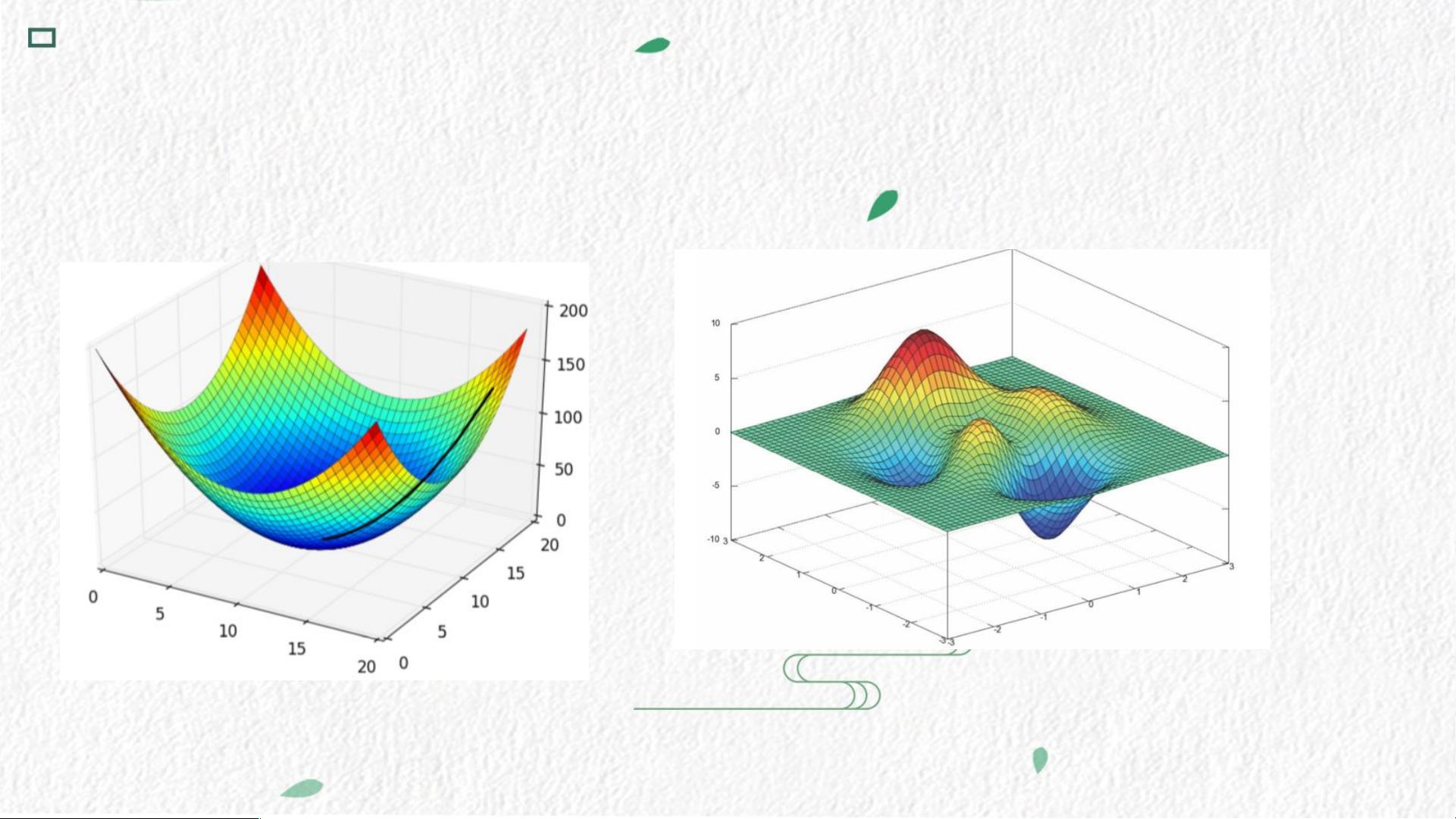
"梯度下降算法.pptx" 梯度下降是一种优化算法，广泛应用于机器学习领域，特别是解决无约束优化问题。它通过迭代的方式寻找损失函数的最小值，是求解模型参数的主要方法之一。从优化算法的发展历史来看，梯度下降在机器学习中的地位至关重要，因为它能有效地处理复杂的多维函数。 在数学上，对于一维的凸函数，我们可以直接通过求导数并令其等于零来找到最小值。对于非凸函数，可能有多个极值点，需要计算每个极值点处的函数值来确定最小值。在高维空间，即多元函数的情况下，我们不仅需要求偏导数，还可能需要考虑海森矩阵来避免鞍点和极大值点。然而，计算机无法直接一次性求出答案，这就需要用到迭代算法。 迭代算法的核心在于重复执行一组指令，每次迭代更新变量的值。梯度下降作为迭代算法的一种，根据当前位置的梯度负方向移动，模拟下山的过程。每一步都向着损失函数下降最快的方向前进。这种直观的解释揭示了梯度下降可能陷入局部最优解，而非全局最优解。如果损失函数是凸的，那么梯度下降法将保证找到全局最优解。 梯度下降有多种变体，包括批量梯度下降（Batch Gradient Descent），其中每次迭代都使用所有数据样本；随机梯度下降（Stochastic Gradient Descent），每次迭代只用一个样本；以及小批量梯度下降（Mini-Batch Gradient Descent），每次迭代用一小部分样本。这些变体在实际应用中各有优势，例如，随机梯度下降在大数据集上计算效率更高，但可能引入更多噪声。 在机器学习模型训练中，如逻辑回归、支持向量机、神经网络等，梯度下降被用来优化模型的权重或参数。通过反向传播计算损失函数关于参数的梯度，然后更新参数以减小损失。此外，为了加速收敛，还可以调整学习率（Learning Rate）或者采用优化器，如动量（Momentum）、自适应学习率算法（如Adagrad、RMSprop、Adam等）。 梯度下降是机器学习中不可或缺的工具，它在理论和实践上都有着深远的影响。理解并掌握梯度下降及其变体，对于理解和构建有效的机器学习模型至关重要。