MATLAB实现数字信号处理：抽样与系统响应

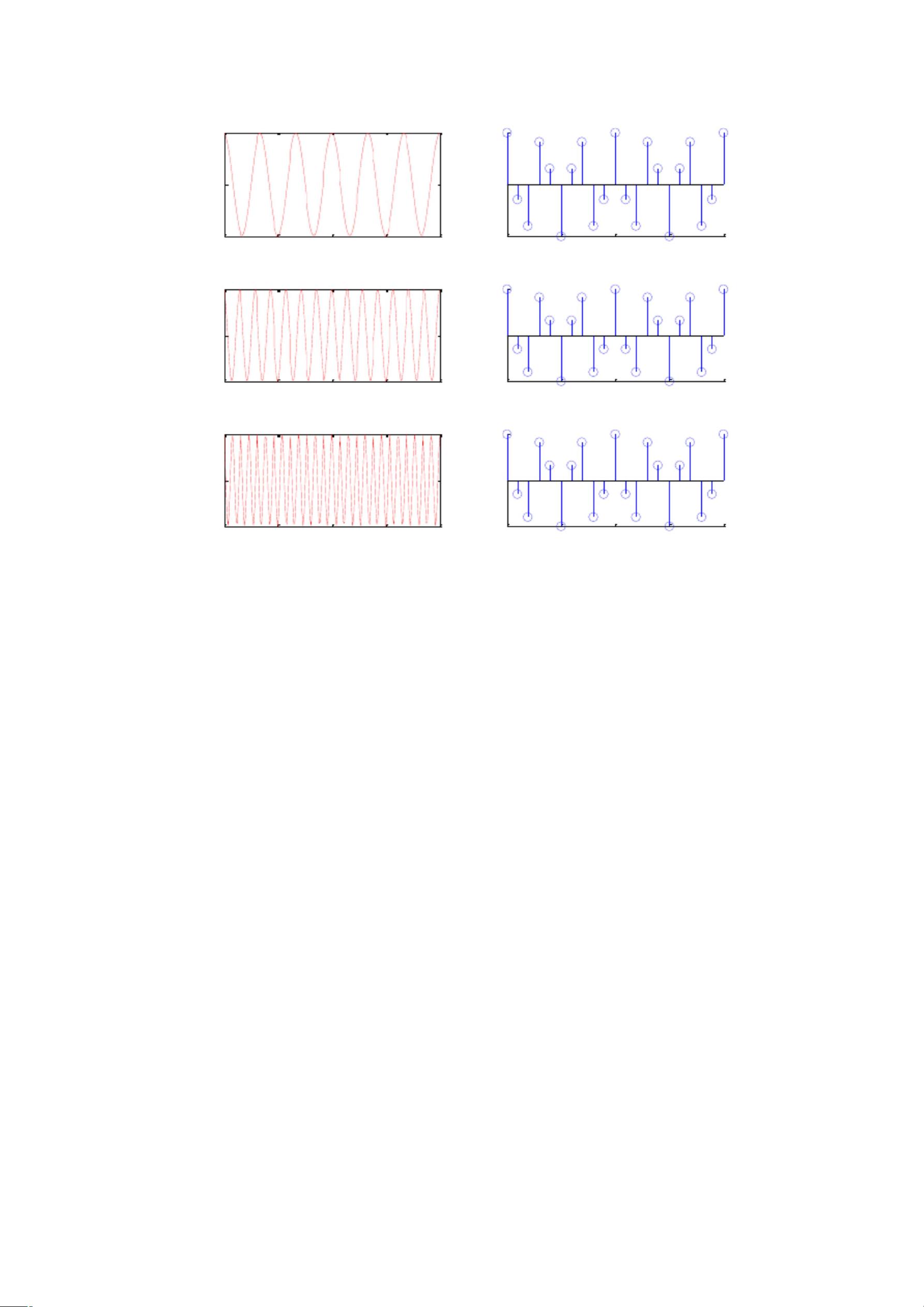
"该文档是关于数字信号处理的MATLAB上机实验指导，涉及了信号抽样、系统响应计算及频域分析等核心概念。实验中使用MATLAB绘制了不同频率余弦信号的时域表示，并通过filter函数计算了系统的响应。此外，还提到了离散系统的频率响应特性的求解方法。" 在数字信号处理领域，MATLAB是一个常用工具，它提供了丰富的函数库来处理各种信号问题。本实验主要分为两个部分：时域分析和频域分析。 首先，实验中提到了信号的抽样。抽样是将连续时间信号转化为离散时间信号的过程，这是数字信号处理的基础。在这里，针对三个余弦信号g1, g2, g3 (频率分别为6π rad/s, 14π rad/s, 和26π rad/s) 进行了抽样，抽样频率设为10Hz。根据奈奎斯特定理，为了无损地恢复原始信号，抽样频率至少应为信号最高频率的两倍，即20Hz。然而，实验中选择的10Hz抽样频率会导致混叠现象，这意味着不能完全无失真地重构原始信号。MATLAB中的`stem`函数用于绘制抽样点，而`plot`函数则用来显示连续信号。 接着，实验展示了如何计算系统响应。在MATLAB中，`filter`函数被用来实现线性时不变系统的卷积运算，求得系统响应h(n)。例如，给定输入信号x(n)和系统参数a2=[1,-1.85,0.85]，`filter`函数计算了系统响应y2。在时域中，可以观察到系统如何影响输入信号的形状和幅度。 最后，实验提到了离散系统的频域分析。频域分析是了解系统频率响应特性的关键，这对于滤波器设计和信号滤波至关重要。MATLAB提供了`firls`函数来设计IIR滤波器，它可以生成一个线性相位滤波器，具有指定的频率响应特性。`firls`函数需要输入滤波器阶数和通带、阻带边界频率，返回的滤波器系数可以用于计算频率响应。 通过这个实验，学生能够深入理解数字信号处理的基本概念，包括信号抽样、系统响应计算和频域分析。同时，掌握了MATLAB在这些任务中的应用，为后续更复杂的信号处理工作打下了坚实基础。