基于Matlab的DFT信号检测和谱分析

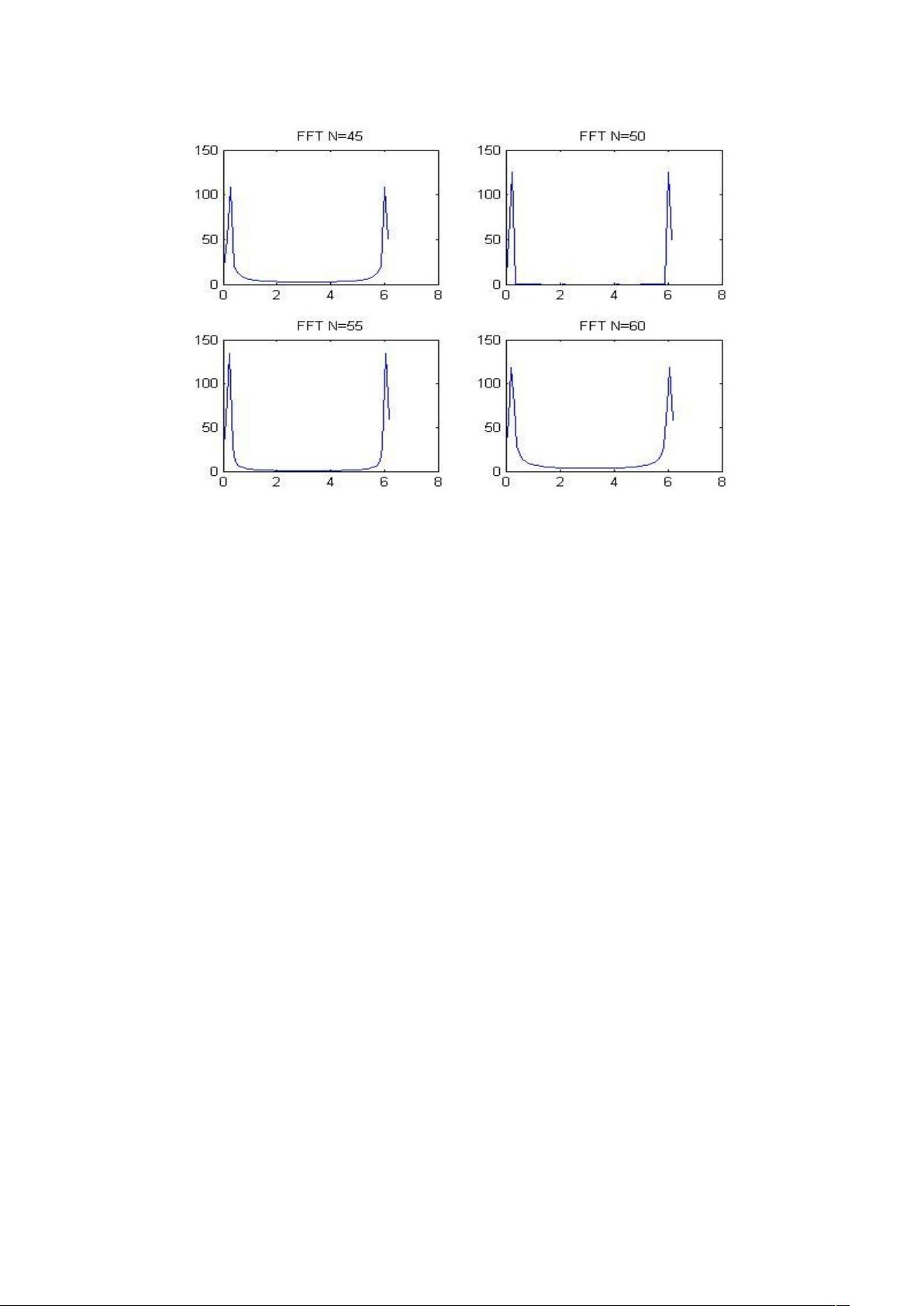
Matlab DFT实现与信号检测及谱分析 一、DFT函数的用法 DFT（Discrete Fourier Transform，离散傅里叶变换）是一种常用的信号处理技术，用于将时域信号转换为频域信号。Matlab中实现DFT函数的用法可以通过使用`dft()`函数来实现。该函数可以将输入信号转换为频域信号，并输出对应的频谱。 二、信号检测及谱分析 信号检测是信号处理的重要步骤之一，DFT可以用于检测信号中的频率成分。通过将信号转换为频域信号，可以观察信号中的频率成分，从而实现信号检测。例如，在上述实验程序中，使用DFT计算信号功率谱，并绘制频谱图，以观察信号中的频率成分。 三、信号截取长度对谱分析的影响 信号截取长度对谱分析的影响是非常重要的。通过改变信号截取长度，可以观察信号频谱的变化。例如，在上述实验程序中，通过改变N的值，可以观察信号频谱的变化。当N增加时，信号频谱变得更加精细，可以观察到信号中的更多频率成分。相反，当N减少时，信号频谱变得更加粗糙，可能会遗漏一些频率成分。 四、DFT点数对谱分析的影响 DFT点数也是影响谱分析的重要因素。通过改变DFT点数，可以观察信号频谱的变化。例如，在上述实验程序中，通过改变N的值，可以观察信号频谱的变化。当DFT点数增加时，信号频谱变得更加精细，可以观察到信号中的更多频率成分。相反，当DFT点数减少时，信号频谱变得更加粗糙，可能会遗漏一些频率成分。 五、采样频率对谱分析的影响 采样频率也是影响谱分析的重要因素。通过改变采样频率，可以观察信号频谱的变化。例如，在上述实验程序中，通过改变采样频率，可以观察信号频谱的变化。当采样频率增加时，信号频谱变得更加精细，可以观察到信号中的更多频率成分。相反，当采样频率减少时，信号频谱变得更加粗糙，可能会遗漏一些频率成分。 DFT函数的用法、信号截取长度、DFT点数和采样频率都是影响谱分析的重要因素。通过改变这些参数，可以观察信号频谱的变化，并实现信号检测和谱分析。