哈夫曼编码与最优二叉树解析

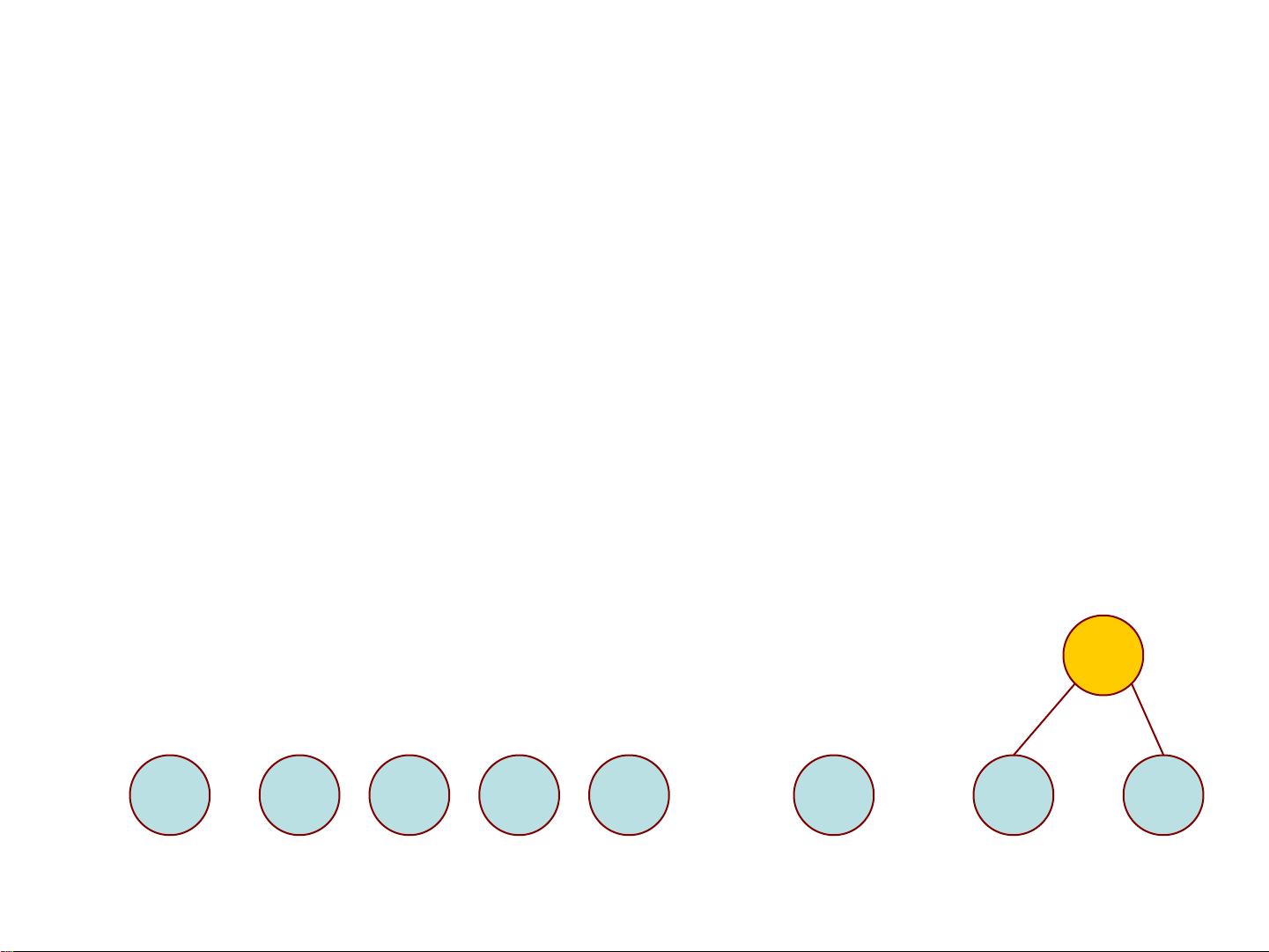
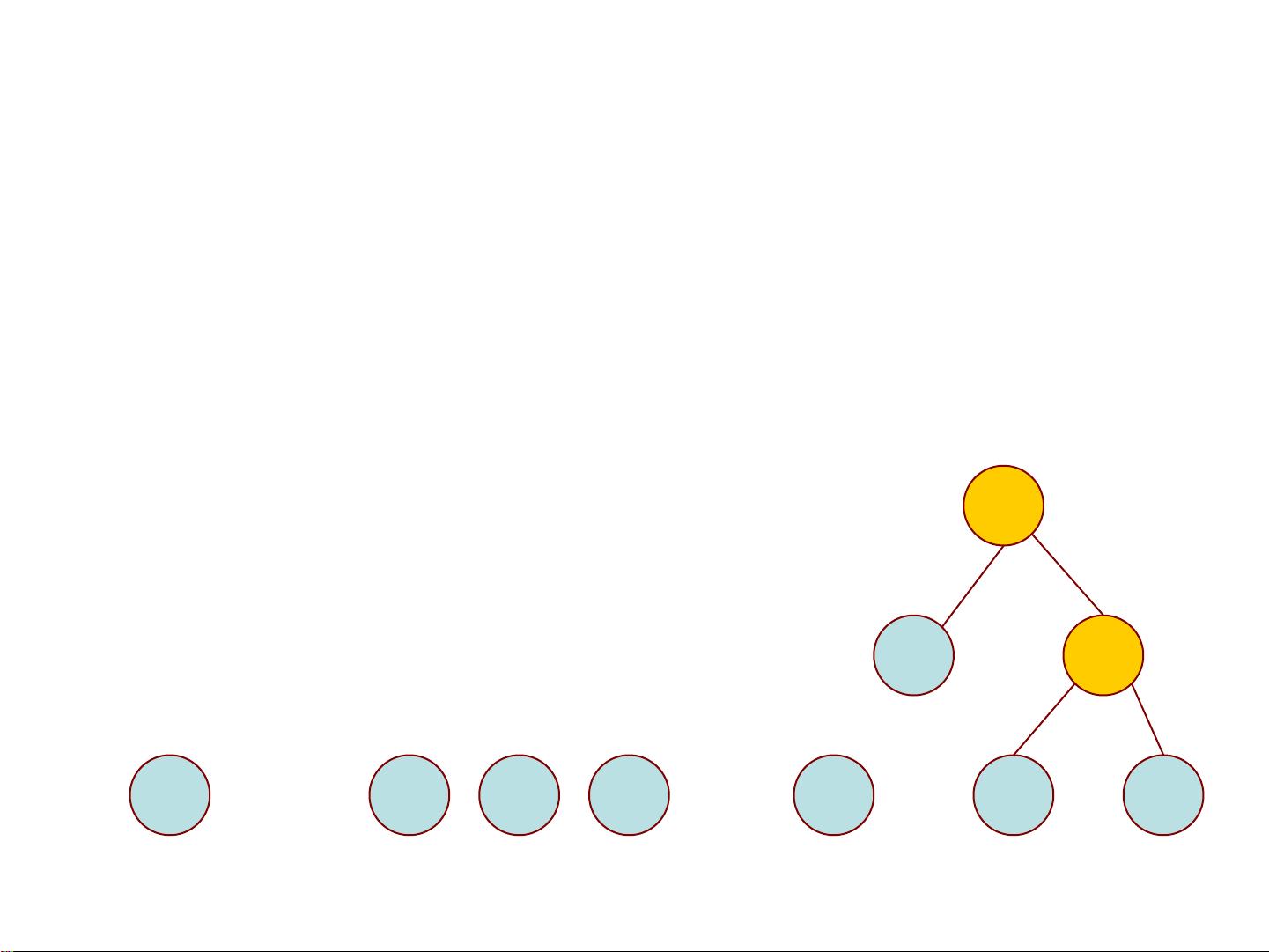
"哈夫曼编码 (44页).pdf" 哈夫曼编码是一种用于数据压缩的高效编码方法，由美国计算机科学家大卫·哈夫曼在1952年提出。这种编码方式利用了频率较高的字符用较短的编码、频率较低的字符用较长编码的原理，以达到对数据进行无损压缩的目的。哈夫曼编码的核心是构建哈夫曼树，这是一种特殊的二叉树结构，也称为最优二叉树。 1. **哈夫曼树的基本概念** - 哈夫曼树是由n个带有权值的叶子节点构建而成的二叉树，这些叶子节点代表了要编码的数据符号，权值通常表示符号的出现频率或重要性。 - 树的目的是最小化所有叶子节点的带权路径长度（WPL），即每个字符的编码长度乘以其出现频率的总和。 2. **最优二叉树的特性** - 权值越小的叶子节点离根节点越远，这确保了频繁出现的字符有较短的编码。 - 哈夫曼树是唯一的，对于给定的节点权值，构建出的哈夫曼树是唯一的，这保证了编码的一致性和可逆性。 3. **哈夫曼树的构造方法** - 贪心策略：每次选取权值最小的两个节点合并，形成一个新的内部节点，其权值为两个子节点的权值之和。 - 自底向上：从所有单个节点开始，逐步通过合并最小的节点构建树，直至只剩下一棵树，这个过程共需合并n-1次。 4. **哈夫曼编码的步骤** - 初始化：将每个字符看作一个独立的树，每个树只有一个叶子节点，对应字符及其权值。 - 合并：反复将当前权值最小的两棵树合并，形成新的内部节点，直到所有树合并成一棵树。 - 编码：从根节点到每个叶子节点的路径形成该叶子节点的编码，通常左分支代表0，右分支代表1。 - 译码：根据编码表，可以将哈夫曼编码解码回原始数据。 5. **示例** - 给定权值为{2,3,4,11}的4个叶子节点，通过多次合并，最终得到最小带权路径长度为34的哈夫曼树。 - 对于8个叶子节点，权值W={5,29,7,8,14,23,3,11}的情况，通过一系列合并，逐步构建出哈夫曼树，最终形成对应的编码表。 哈夫曼编码广泛应用于文本、图像、音频等多种数据的压缩，例如在ZIP、GIF、JPEG等文件格式中都有应用。通过哈夫曼编码，可以有效地减少存储空间，提高数据传输效率，同时保持数据的完整性，因为它是无损的。在实际应用中，哈夫曼编码不仅可以单独使用，也可以与其他压缩算法结合，以实现更高效的压缩效果。