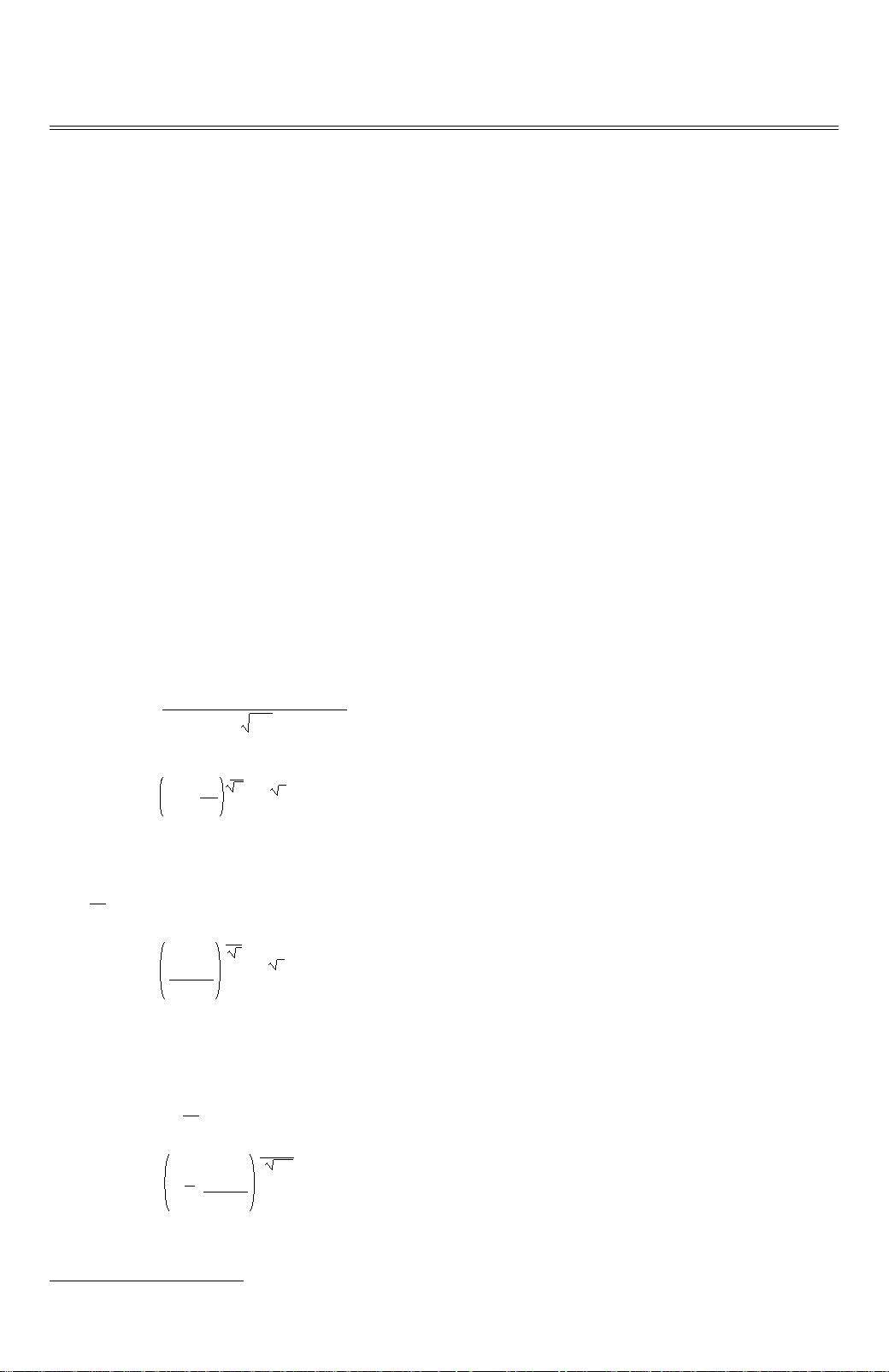独立同分布随机变量序列的部分和乘积渐近性质探讨

"该文是关于部分和乘积渐近性的一个自然科学论文，作者臧庆佩探讨了独立同分布平方可积随机变量序列的部分和乘积的渐近正态性质。文章引用了先前的研究成果，包括Arnold和Villasenor的工作，以及Rempala和Wsolowski与另一篇文献中的定理，涉及Gumbel分布、标准正态随机变量、Stirling公式和对数正态分布。" 正文: 本文主要关注的是随机变量序列的部分和乘积的渐近行为，特别是当这些变量独立同分布且平方可积时。在概率论和统计学中，这种类型的序列有着广泛的应用，例如在大数定律和中心极限定理等领域。作者臧庆佩基于前人的研究成果，深化了这部分理论。 首先，文章提到了由Arnold和Villasenor研究的情况，其中随机变量X1服从Gumbel分布。在这种情况下，当序列长度n趋近于无穷大时，部分和的对数（即∑_{k=1}^{n} log(S_k) - n log(n) + n / 2^n）会按照一个标准正态分布N(1)收敛。这个结果揭示了序列的部分和乘积在大样本情况下的统计特性。 随后，引用了Rempala和Wsolowski的定理，该定理扩展了这一理论，指出当序列中的随机变量都是正的，且具有相同的期望值μ和变异系数γ时，部分和的乘积除以适当的标准化常数后，会按照e^2N(1)分布收敛，这里的N(1)表示标准正态分布。 文献中还进一步引入了一个更精确的渐近表达式，即定理2，它考虑了独立同分布的正的平方可积随机变量的三角组列。在这种情形下，当n趋近于无穷大时，部分和的乘积除以适当的标准化项后，按照eN(1/log(n))分布收敛。这表明部分和乘积的渐近行为随着序列结构的变化而变化，但依然保持着正态分布的形式。 此外，作者还引用了引理1，这是支持上述定理的一个关键工具，通常用于证明这类渐近性质的推导过程。通过对随机变量序列的深入分析，论文提供了对部分和乘积渐近正态性质的深入理解，这对于概率论、统计推断以及相关应用领域（如风险管理和金融工程）具有重要的理论价值。 这篇论文通过深入研究独立同分布随机变量序列的部分和乘积的渐近性质，不仅丰富了现有的概率理论，也为实际问题中处理大规模随机数据提供了理论基础。其结果不仅适用于理论研究，也对那些需要理解和模拟复杂随机现象的实际应用提供了指导。