数值分析：插值法与曲线拟合关键介绍

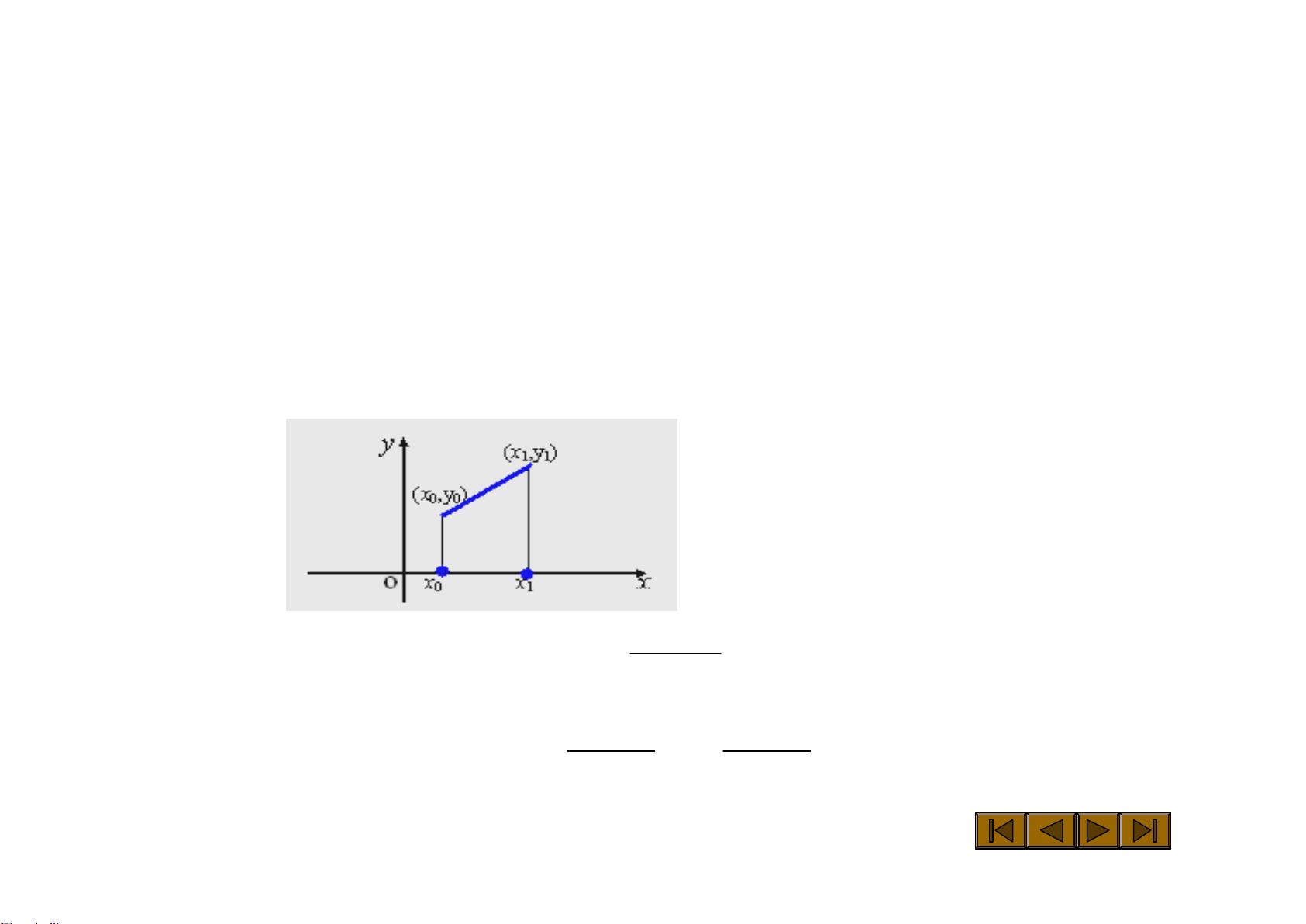
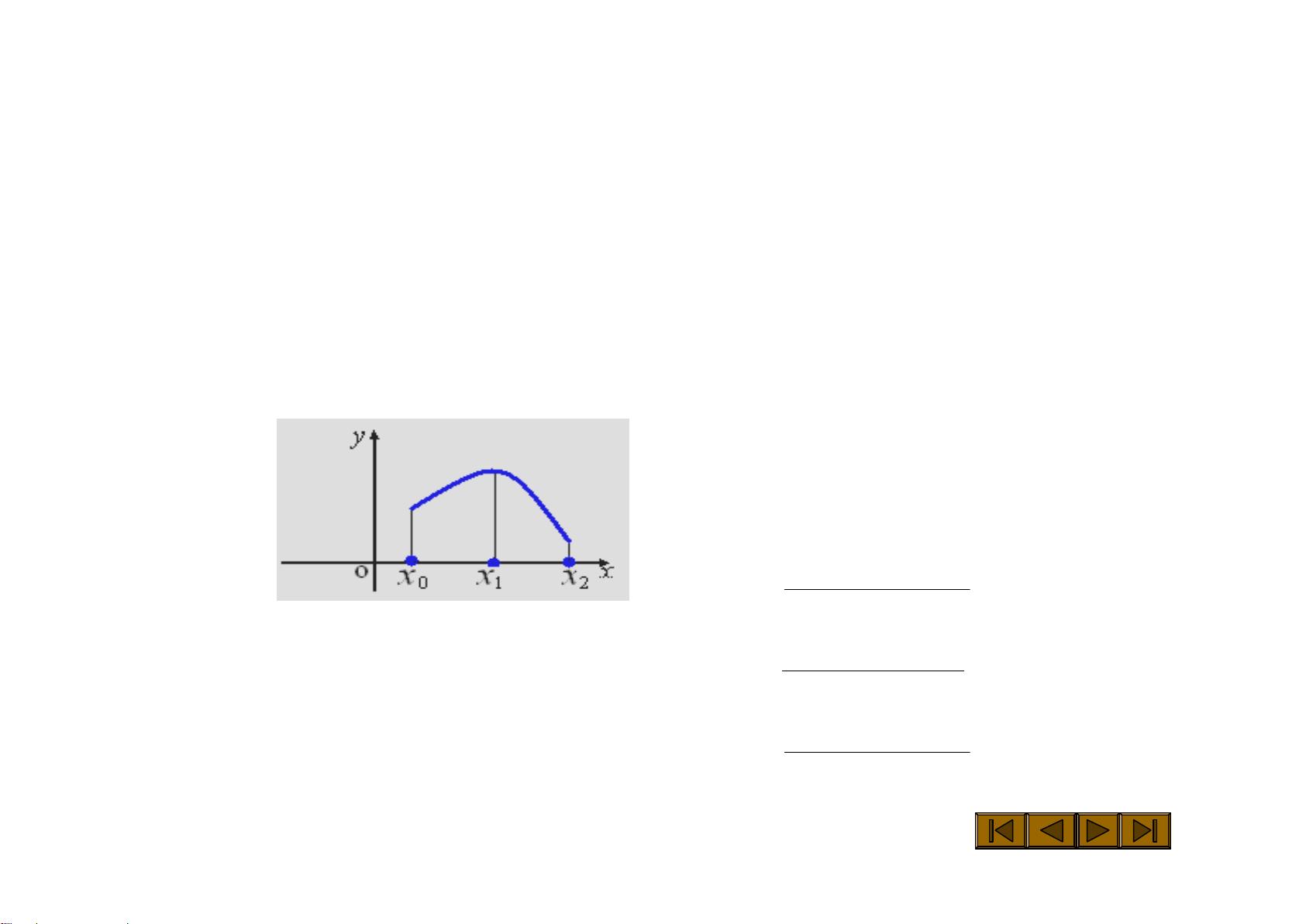
数值分析是一门研究如何用数值方法求解数学问题的学科，特别是在那些解析解难以求得或者计算成本过高的情况下。本复习资料主要围绕插值法展开，这是一种重要的数值近似技术，用于在给定一组离散点的数据基础上构建一个连续的函数模型，以便于分析和计算。 第二章详细介绍了几种常用的插值方法： 1. 拉格朗日插值多项式：这种方法通过构建一组特定的多项式，使得每个多项式的值在给定的插值节点处等于对应的数据点。拉格朗日插值的构建依赖于拉格朗日基函数，每个基函数仅在该节点处为1，其他节点为0。 2. 牛顿插值多项式：这是另一种基于多项式插值的方法，它利用了牛顿公式来构造插值多项式。牛顿插值更高效，但计算过程可能会更复杂。 3. 分段低次插值：针对函数在不同区间有不同的行为，将区间划分为若干部分，每部分内用低次多项式近似，这种方式称为分段插值，确保在各段内的精度和整体连续性。 4. 三次样条插值：这种方法使用光滑的三次多项式曲线连接各个插值点，形成平滑的过渡，适合于处理光滑函数的插值，提高了插值的精度和连续性。 5. 曲线拟合的最小二乘法：不同于插值，最小二乘法允许使用非插值函数，目标是找到一个函数，使得它在所有给定点上的误差平方和最小。这种方法在实际应用中非常普遍，例如在统计学和数据分析中。 插值法的应用广泛，不仅限于理论研究，也常用于工程设计、数据分析和计算机图形学等领域。它能够处理连续变量问题的离散化处理，如数值积分、微分和解决差分方程，以及在有限元方法中对复杂函数进行近似。通过插值和曲线拟合，我们可以构造出既体现原函数特性又便于计算机运算的简单函数，极大地简化了数值计算的复杂度。