分治法求解最近点对问题——实验报告

"深圳大学算法设计与分析实验报告，实验二分治法求最近点对问题，由沈晨玙完成，计算机与软件学院，计算机科学与技术专业，指导教师杨烜。实验内容包括使用蛮力法和分治法计算平面上N个点的最短距离，对比不同N值下两种方法的运行时间，并可能通过图形界面展示算法执行过程。" 在本次实验中，主要探讨了如何解决平面上给定的N个点之间的最短距离问题。实验的目的在于理解和应用分治法来解决这个问题。实验的具体内容分为以下几个部分： 1. **最短距离计算**：给定N个点，任务是找到其中两点间最短的距离。输入是N个点的坐标，输出是最短距离的点对。 2. **蛮力法实现**：通过遍历所有点对，计算每一对之间的距离并找出最小值。这种做法的时间复杂度为O(N^2)。 - **伪代码**：对于N个点，用两层循环遍历所有点对，计算距离并保存最小值。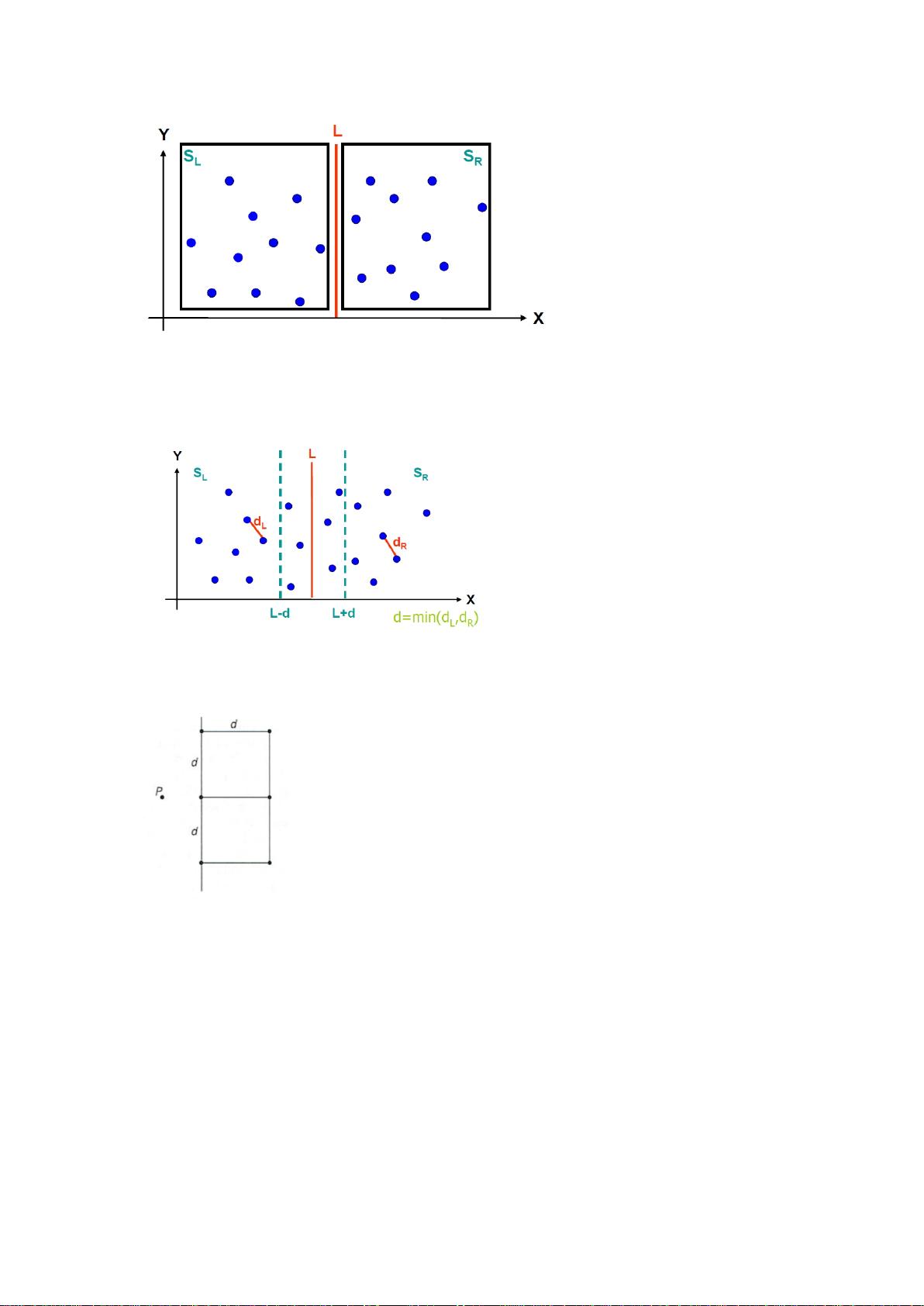 ```python for i in range(N): for j in range(i+1, N): distance = calculate_distance(point[i], point[j]) if distance < min_distance: min_distance = distance closest_pair = (point[i], point[j]) ``` 3. **分治法实现**：当点的数量较大时，采用分治策略提高效率。主要步骤包括预处理、分割、递归和合并。 - **预处理**：先按x轴和y轴对点进行排序。 - **分割**：选择一个分割线L，将点集分为大致相等的两半SL和SR。 - **递归**：分别在SL和SR中递归寻找最短距离，得到dl和dr。 - **合并**：取min(dl, dr)，在分割线两侧扩展d，形成边界区域Y，然后按y轴对Y中的点进行排序。对Y'L中的每个点，线性效率地检查Y'R中的点，更新最近距离。 分治法的关键在于第6步，通过排序和巧妙的点对比较，可以在线性时间内找到边界区域内最近的点对，避免了平方级的时间复杂度。 4. **性能分析**：通过比较N=100000到1000000时蛮力法和分治法的运行时间，评估实际效率与理论效率的差异，并对两种方法的效率进行分析。 5. **图形界面**：如果能够将算法执行过程可视化，可以额外加分，有助于理解算法的运作。 实验结果显示，对于小规模数据，蛮力法和分治法得到的结果一致，但在大规模数据上，分治法的优势明显，因为它降低了时间复杂度，提高了算法效率。实验报告中还应详细记录了每一步的执行过程和效率分析。