元胞自动机理论与应用

"元胞自动机理论基础，适用于学习编程，尤其是C语言的学员，是单片机和游戏编程的基础。元胞自动机是一种离散动力系统，由散布在规则网格上的元胞组成，每个元胞状态有限且同步更新，遵循局部规则。自动机的概念源自图灵机，用于模拟计算过程和复杂系统的行为。" 元胞自动机（Cellular Automata，CA）是计算机科学和理论物理中的一个重要概念，它提供了一种模型化复杂系统演化的手段。在这个理论中，大量的元胞在二维或更高维度的格网上分布，每个元胞拥有有限数量的离散状态，并根据相邻元胞的状态和一组固定的局部规则进行同步更新。这种简单的规则集可以导致极其复杂的行为模式，使得元胞自动机成为研究自组织、混沌、生命现象以及各种自然和社会系统动态的理想工具。 自动机的起源可以追溯到英国数学家阿兰·图灵（Alan Turing）在1936年提出的图灵机模型，这是一种理论计算设备，能够模拟任何可计算函数。图灵机包含一个有限控制器、无限长的存储带和读写头，能够执行基本的移动、读写和控制操作。它是现代计算机科学的基石，定义了计算的普遍性。 元胞自动机与图灵机的主要区别在于它们对存储带的处理：图灵机拥有无限长的存储带，而有限带自动机（如有限状态机）的存储是有限的。元胞自动机因其局部性和并行性，能够有效地模拟自然界中的许多现象，如生物生长、扩散过程、交通流和生态系统动态。 在编程领域，元胞自动机的概念对于理解和实现单片机系统以及游戏逻辑至关重要。单片机往往需要高效地处理有限的资源和简单的交互规则，这与元胞自动机的基本原理相吻合。此外，元胞自动机的并行性质使其在并行计算和分布式系统中也有应用潜力。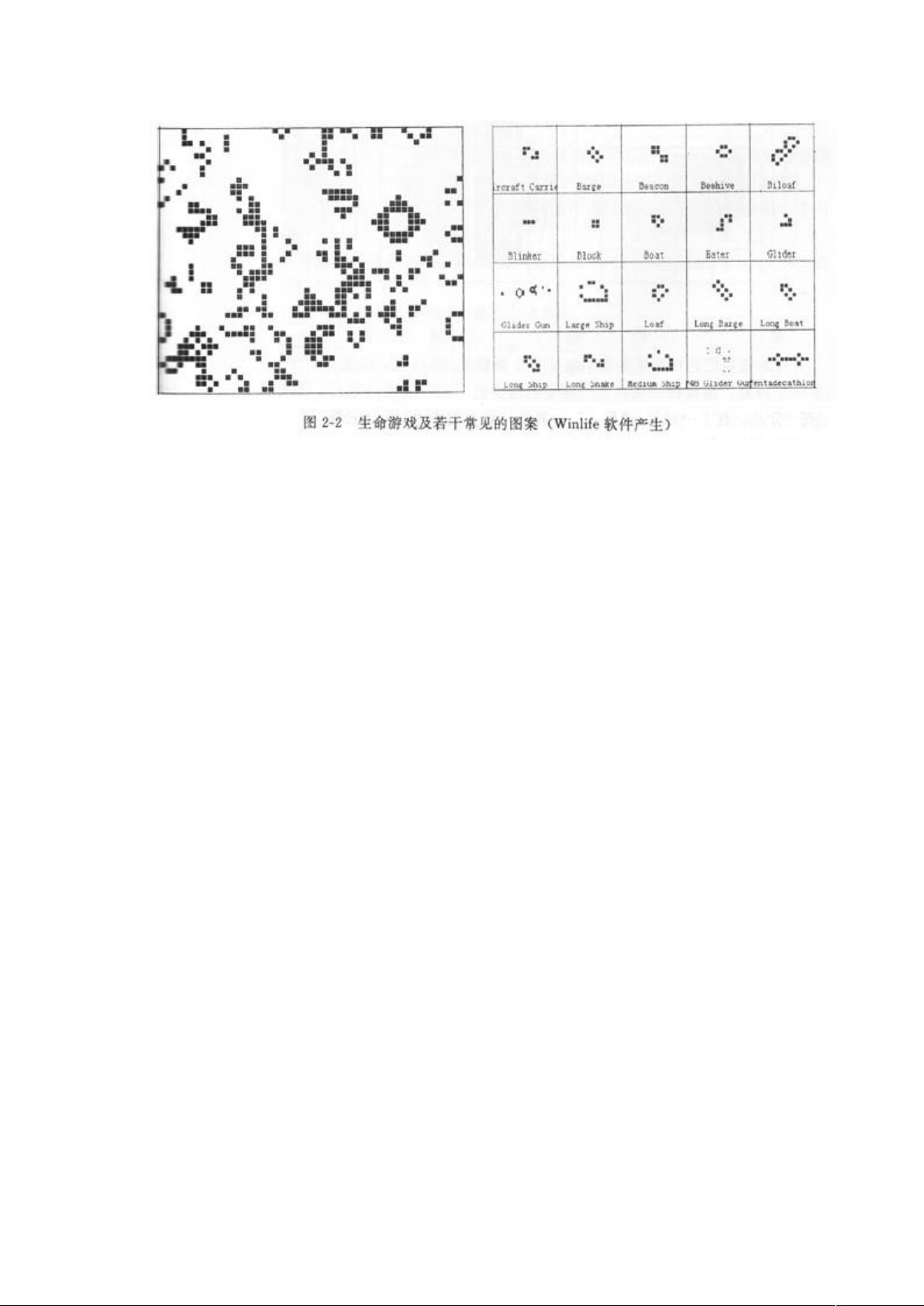 元胞自动机的分类通常基于元胞的状态数量、邻域大小和更新规则的复杂性。最著名的元胞自动机之一是康威的生命游戏（Conway's Game of Life），这是一个二维的、二状态的规则系统，仅基于简单的生与死规则，就能表现出丰富的动态行为，甚至可以模拟出计算能力。 学习元胞自动机不仅可以帮助理解底层计算原理，还能启发新的算法设计和问题解决策略。在C语言或其他编程语言中实现元胞自动机，可以锻炼编程技巧，同时探索如何用简单的规则生成复杂行为。对于想要深入研究计算理论、复杂系统或模拟自然现象的人来说，元胞自动机是一个值得深入研究的领域。