径向基函数网络（RBFN）详解：功能逼近与预测

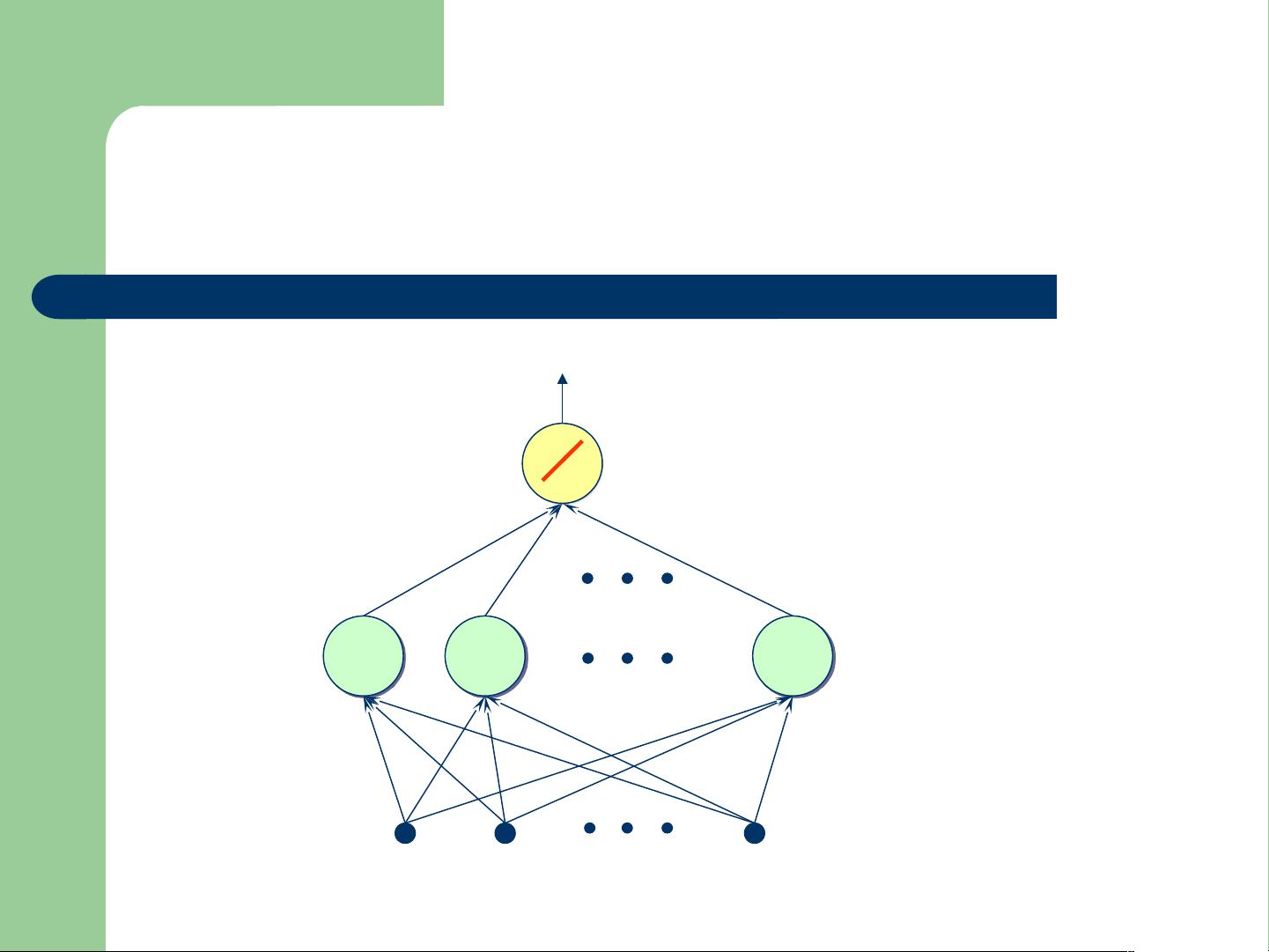
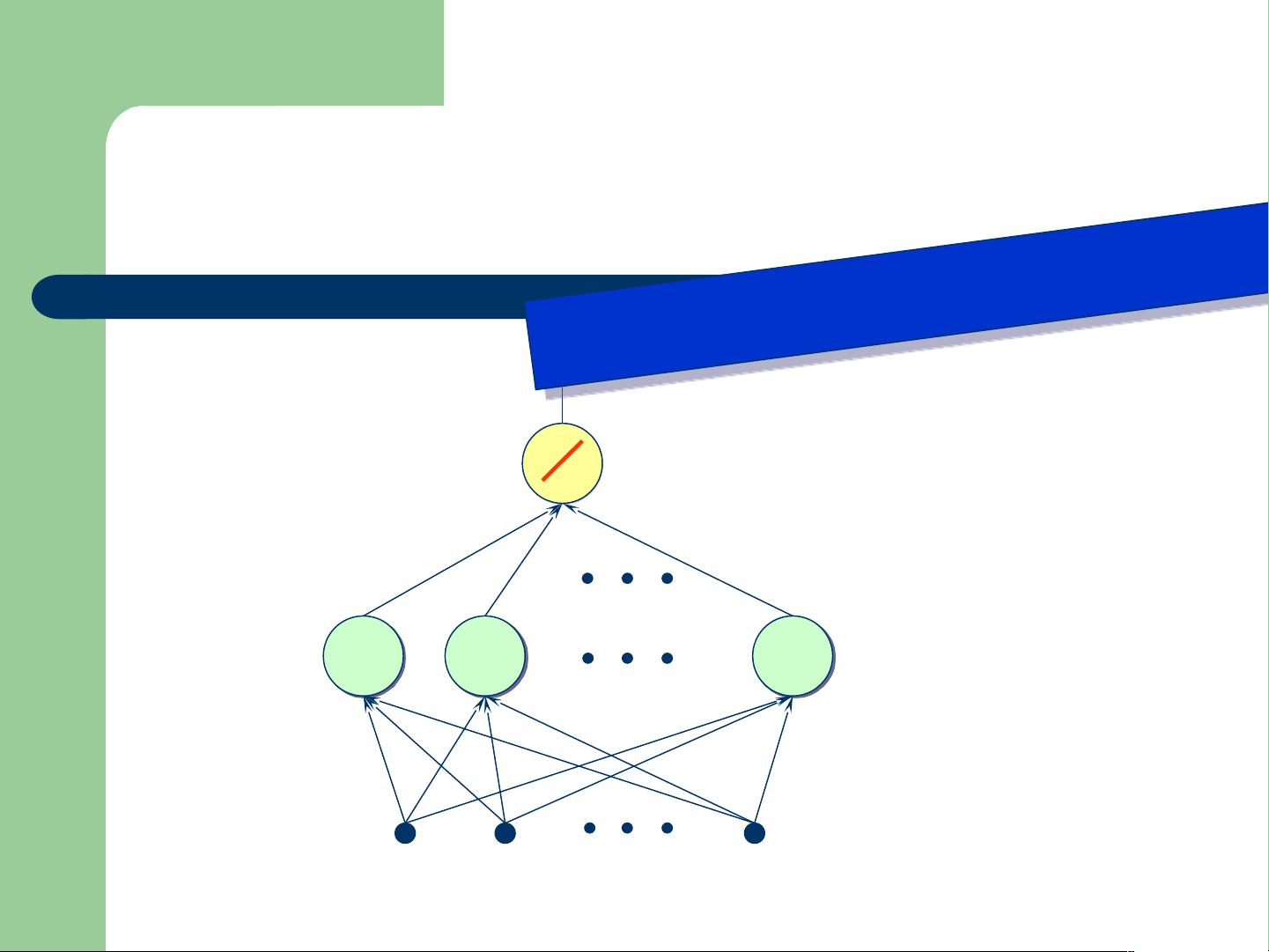
"这篇文档是关于径向基函数网络（Radial Basis Function Networks，简称RBF网络）的介绍，涵盖了其算法、结构以及在函数逼近和预测中的应用。" RBF网络是一种人工神经网络，主要用途包括模式分类、函数近似和时间序列预测。其工作原理基于函数近似，目标是通过学习未知函数f来建立输入X和输出Y之间的映射关系。在函数逼近问题中，给定一组训练样本对{(xi, yi)}，RBF网络的目标是找到一个近似函数^f，使得^f(X)尽可能接近于真实函数f(X)。 RBF网络通常由输入层、隐含层和输出层构成。输入层接收输入数据，隐含层包含一系列的径向基函数单元，这些单元通常使用高斯函数作为基函数，以输入数据的距离为中心进行响应。输出层则通过线性组合隐含层的输出来生成最终的预测值。 对于函数逼近，RBF网络的核心在于隐含层的RBF单元。每个RBF单元负责在一定范围内对输入数据进行响应，形成一个局部的“基”，这些基函数的组合可以覆盖整个输入空间，从而实现全局的函数逼近。投影矩阵则是描述输入数据如何通过RBF单元进行变换的关键概念，它反映了输入数据到隐含层特征空间的映射。 学习RBF网络的过程通常涉及确定中心点（即RBF单元的位置）、选择合适的核函数和确定权重。学习算法可能包括最小二乘法、梯度下降等，目的是最小化预测输出与实际输出的误差。 RBF网络面临着偏差-方差困境，即模型复杂度与泛化能力之间的权衡。增加网络的自由度（如更多的RBF单元）可以提高拟合训练数据的能力，但可能导致过拟合，降低对新数据的预测准确性。因此，有效参数的数量和模型选择是优化RBF网络性能的重要环节。 增量操作在RBF网络中也扮演着角色，允许网络在新数据到来时动态调整，而不需要重新训练整个模型。这在处理流式数据或需要实时更新的场景中尤其有用。 RBF网络作为一种强大的非线性模型，因其在函数逼近和预测任务上的高效性能而被广泛采用。它们的理论基础和实用技巧都在持续发展，以适应不断变化的计算需求和应用领域。