EM算法详解：非完整数据的参数估计利器

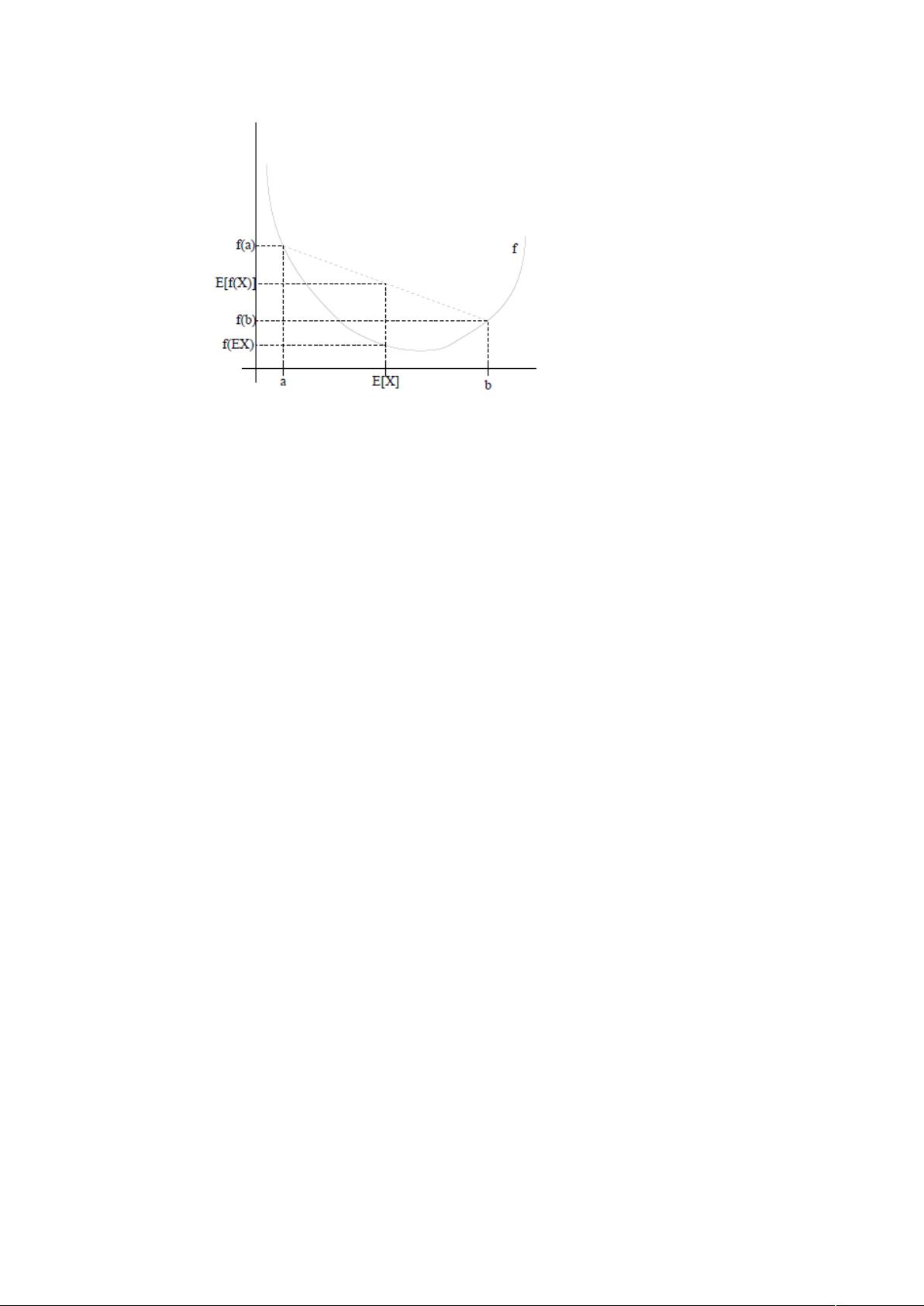
**算法原理** EM(Expectation-Maximization)算法，由Dempster、Laird和Rubin在1977年提出，主要用于处理非完整或缺失数据的参数极大似然估计。该算法的特点是通过迭代的方式在存在隐性变量的模型中估计参数，即使数据不完全，也能找到最接近真实分布的参数值。其核心思想可以比喻为食堂分菜的例子：通过不断调整分配，使得两个碗中的菜尽可能平均。 **算法推导与Jensen不等式** 在算法推导过程中，关键概念之一是Jensen不等式，它是优化理论中的一个基础工具。Jensen不等式表明，如果一个函数f满足凸性条件，即其一阶偏导数存在且二阶偏导数非负（Hessian矩阵半正定），则函数关于其均值的函数值不会小于函数本身。在EM算法中，这个特性帮助我们确保在每次迭代过程中，通过期望(E)步骤得到的参数估计会导向全局最优解。 **应用领域** EM算法在机器学习和数据挖掘中广泛应用，特别是在数据聚类（如Gaussian Mixture Models，GMM）中，通过处理缺失数据，提升模型的准确性和鲁棒性。在GMM中，算法重新审视了混合高斯模型的参数估计问题，特别是当观测数据包含未观测到的隐性成分时。 **Python实现** 学习EM算法时，Python是一个很好的实践平台。Python中有许多库，如scikit-learn，提供了现成的GMM实现，初学者可以通过这些库理解并实现EM算法。从初始化分布参数开始，逐步进行E步（计算隐变量的期望）和M步（更新参数以最大化似然函数），通过反复迭代直至收敛。 **总结** EM算法是解决含有隐变量问题的重要工具，其在实际应用中的价值在于能够处理缺失数据，提高模型的适应性。学习过程中，理解Jensen不等式的直观解释以及算法的迭代过程至关重要。通过Python编程实践，能够加深对该算法的理解和掌握。