图模型与机器学习：概率表示与条件独立性

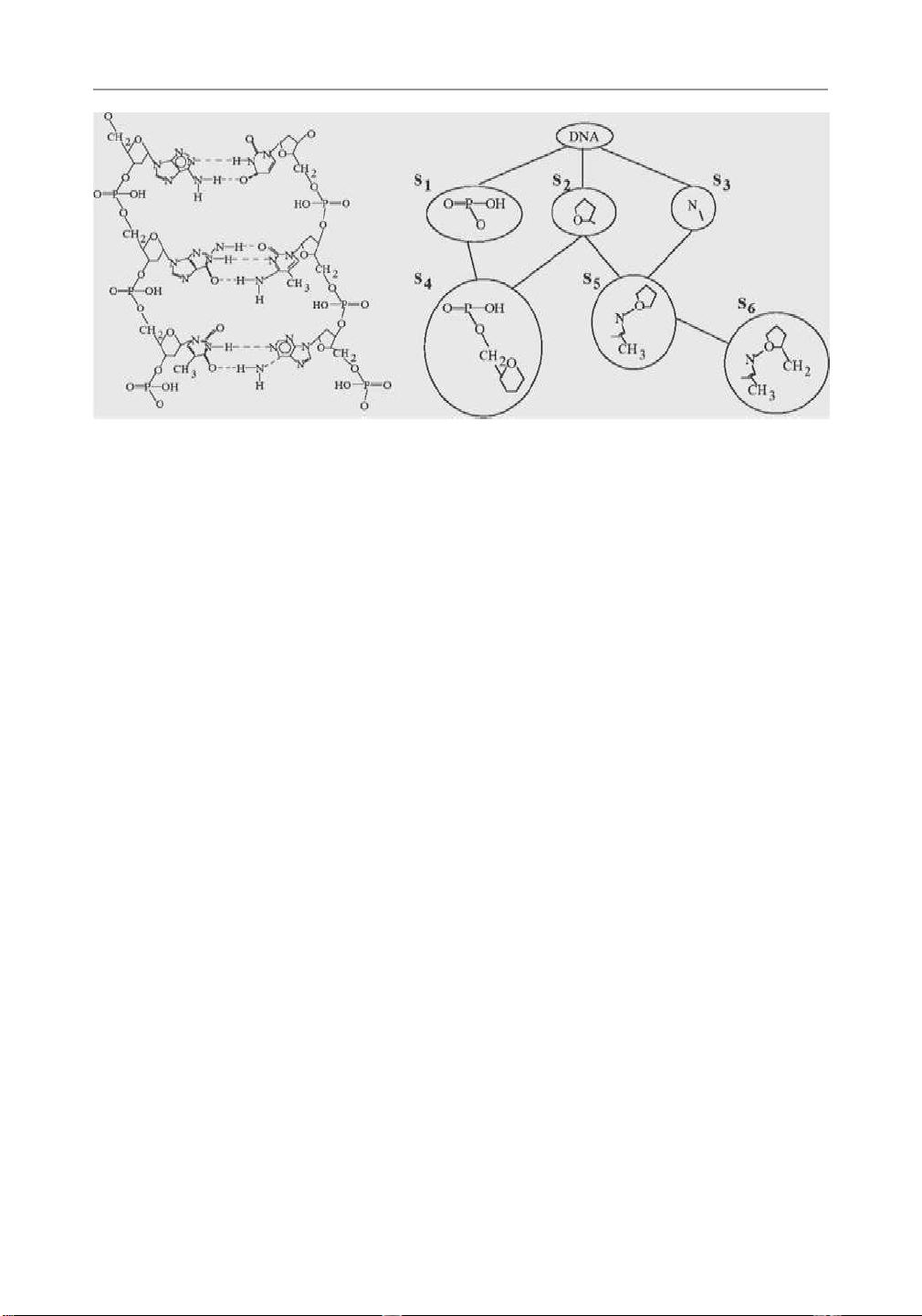
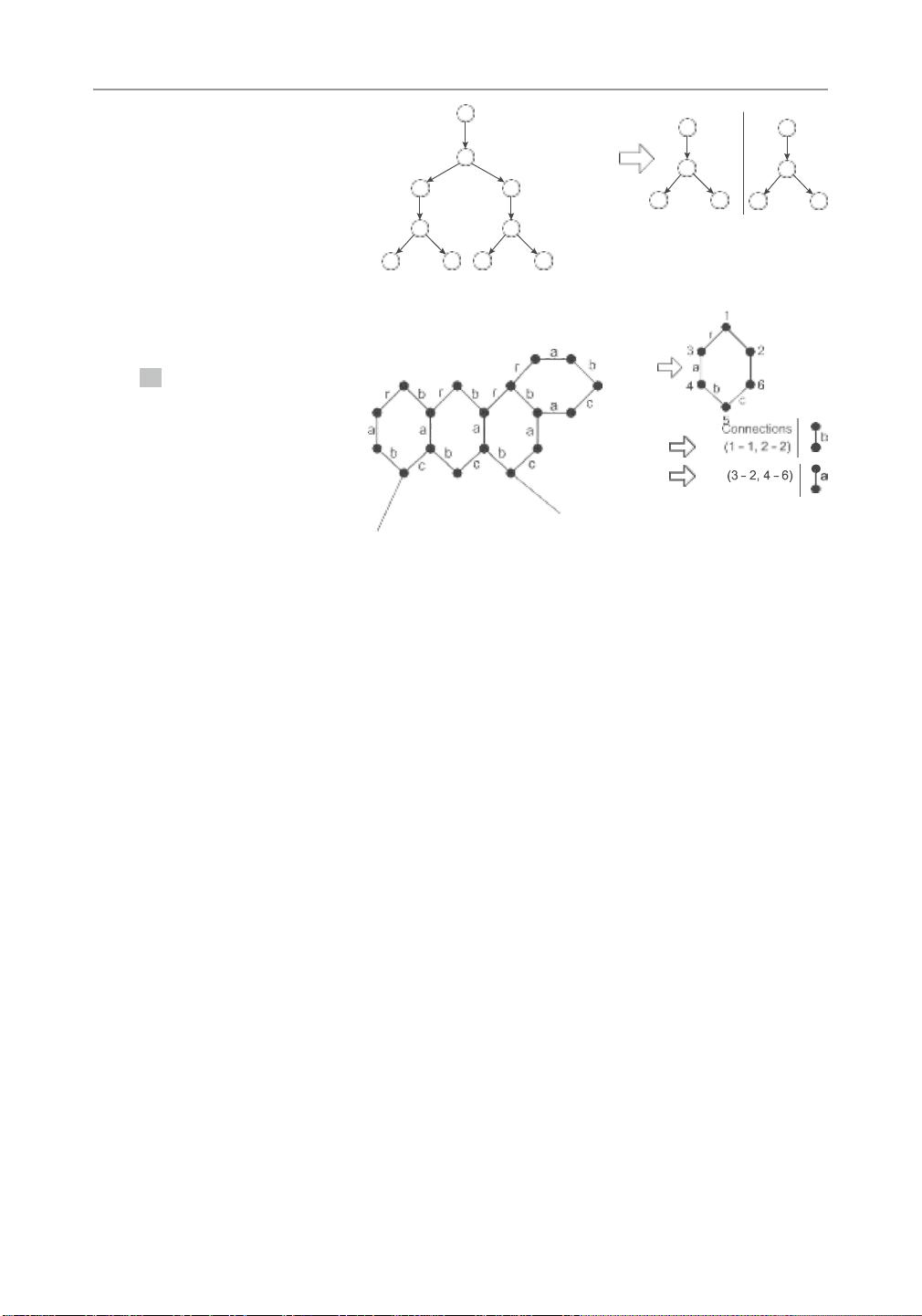
《机器学习与数据挖掘百科全书(第二版)》中文版part4深入探讨了图示模型这一关键概念，这些模型在信息建模、概率推理以及数据分析中起着至关重要的作用。图1展示了图形定义中的三个关键元素：产品规则（定义1），即任何概率分布都可以表示为一个图形模型，其中各变量之间的依赖关系通过边相连；条件独立性（定义3），当两个变量XA和XB在给定XC的条件下相互独立时，表示为XA?XB|XC，意味着它们的联合概率可以分解为各自与XC的条件概率的乘积。 图示模型可以是有向的（如图2左图所示），在这种情况下，箭头指示了因果关系的方向，例如A影响B但反之不成立。无向模型（图2右图）则表示的是更平等的关联，没有方向性。这些模型用于捕捉变量之间的复杂关系，并且在处理高维数据时尤其有用，因为它们允许我们对数据的结构进行抽象，从而高效地计算如特定结果的概率或最可能结果等重要统计特性。 例如，对于一个多变量概率分布，我们可以用向量表示每个随机变量及其取值，如XD = {X1, X2, ..., XN}。通过图的节点和边，我们可以直观地表示出变量间的依赖程度，这对于推断隐含的条件概率以及执行变量的边际化（定义2）至关重要。边际化是指计算单个变量的概率分布，而无需考虑其他变量的值，这对于预测和决策分析非常实用。 在实际应用中，图示模型在诸如计算机视觉中的图像分类、模式识别中的特征选择、经济学中的市场行为分析以及社会科学中的社会网络分析等领域都发挥着核心作用。通过利用分布的结构，我们可以设计高效的算法，如利用分配律将复杂的概率表达式分解为低维度的因子，以便于计算和优化。 《机器学习与数据挖掘百科全书》的这部分内容提供了一个全面的框架，帮助读者理解如何构建和使用图示模型来处理现代大数据背景下的各种问题，并利用这些模型来增强预测性能和解释性。通过掌握这一理论和实践工具，数据分析师和机器学习工程师能够更有效地探索和利用数据中的潜在规律。