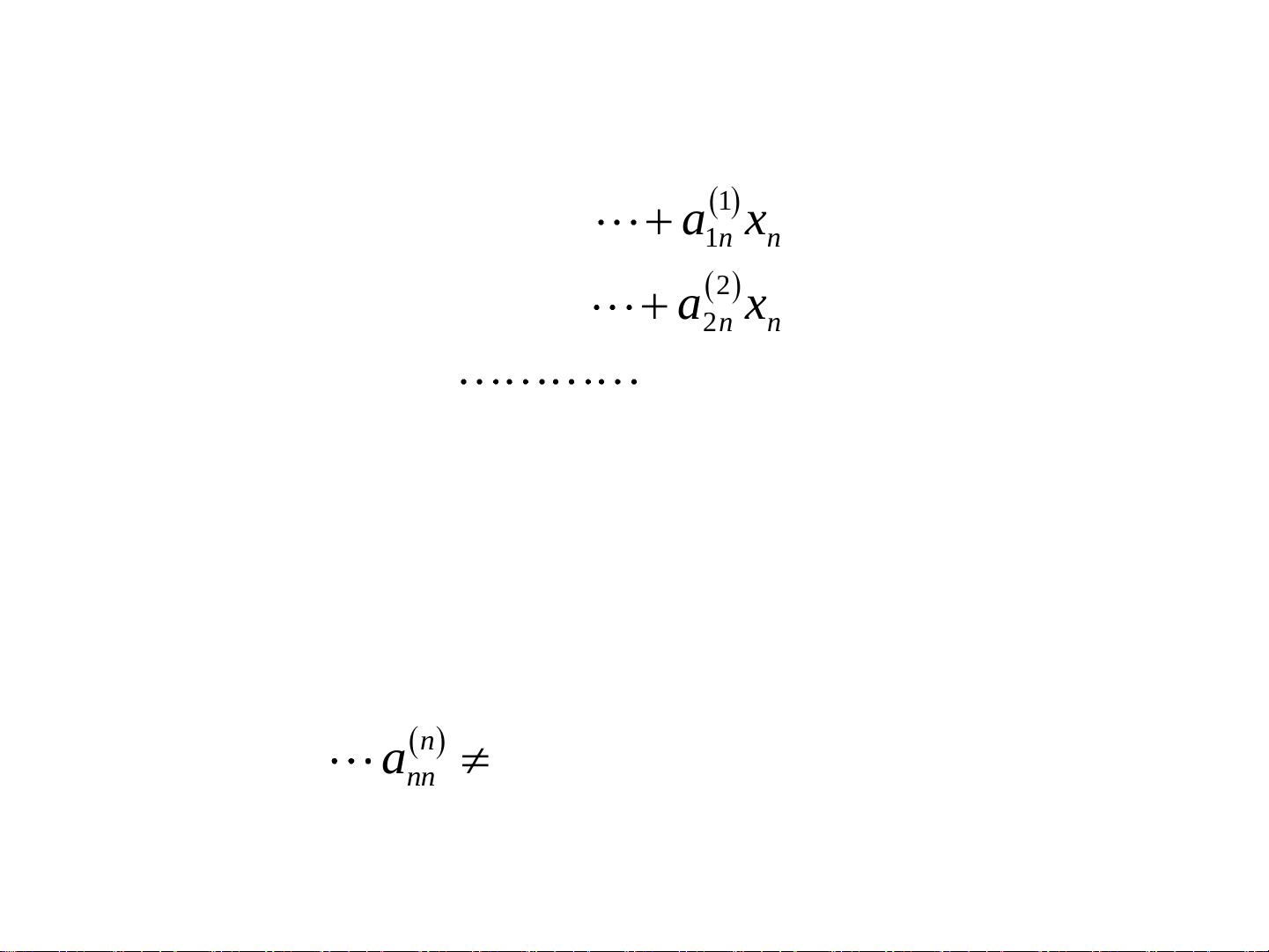
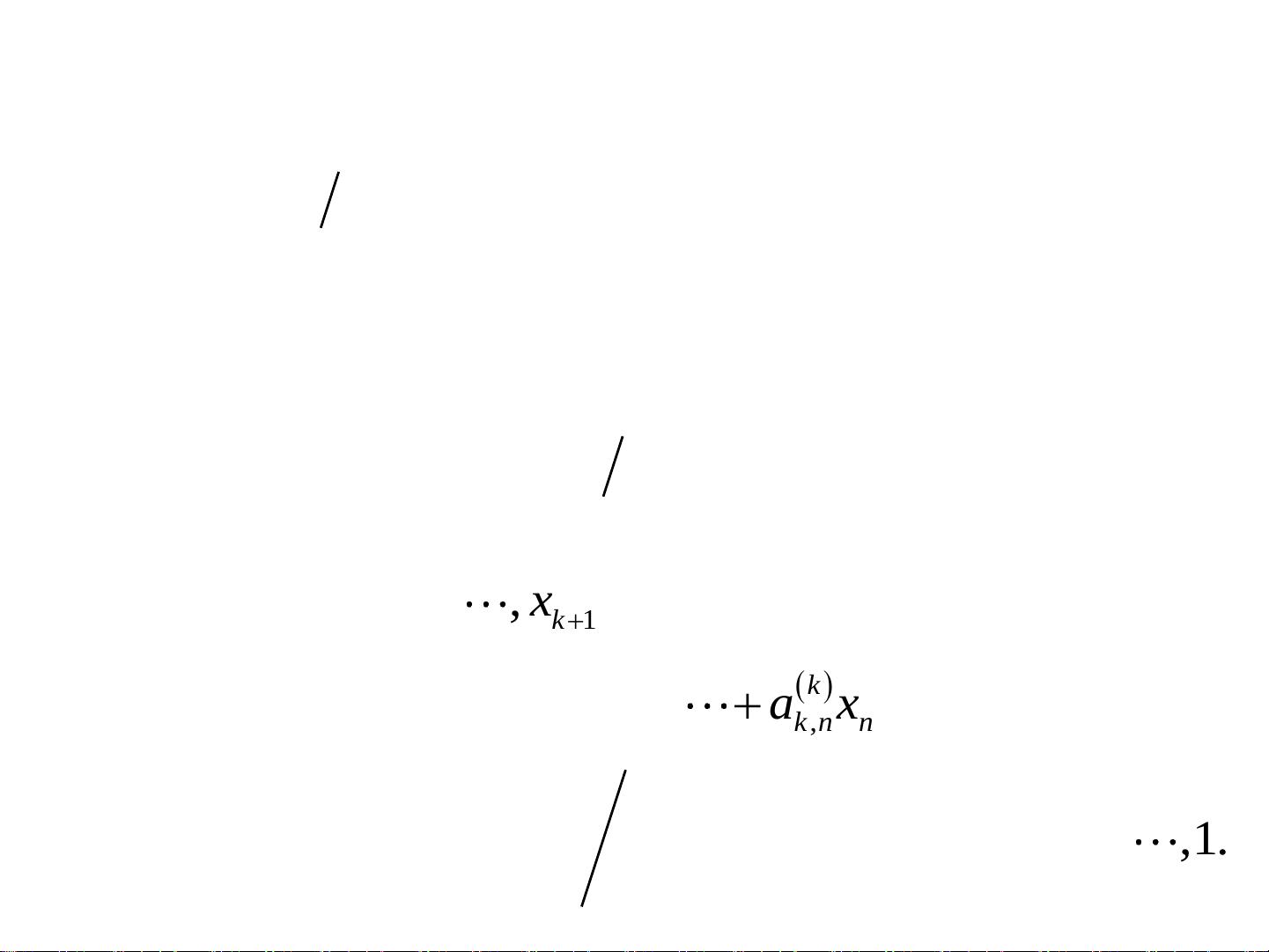
数值分析：线性方程组直接法解析

“数值分析ppt（解线性方程组的直接法）” 在数值分析中，解线性方程组是一项基础且重要的任务，广泛应用于自然科学和工程技术领域。线性方程组通常表示为 \( Ax = b \)，其中 \( A \) 是一个系数矩阵，\( x \) 是未知数向量，而 \( b \) 是已知向量。直接法和迭代法是解决这类问题的两大主要策略。 直接法，如其名，旨在通过一系列无舍入误差的理想运算来求得线性方程组的精确解。然而，在实际计算中，由于舍入误差的存在，我们只能得到近似解。直接法的一个经典例子是高斯消去法，它通过行变换逐步简化系数矩阵，最终将其转化为上三角形或对角形矩阵，从而简化求解过程。此外，还有LU分解法，该方法将矩阵 \( A \) 分解为两个三角形矩阵的乘积 \( L \cdot U \)，然后分别求解 \( Ly = b \) 和 \( Ux = y \)。平方根法和追赶法也是直接法的变体，它们在特定条件下能有效求解线性系统。 迭代法则是一种不同的策略，它通过构造一个递推公式，生成一系列解的近似序列，这些序列逐渐接近线性方程组的精确解。迭代法的优点在于存储需求小和程序设计相对简单，但其收敛性与收敛速度是需要关注的问题。不同的迭代方法，如雅可比法、高斯-塞德尔迭代和共轭梯度法，都有各自的优缺点和适用场景。 在大型线性方程组的求解中，直接法通常适用于方程组规模较小的情况，因为它们通常需要较大的计算量和存储空间。随着未知数数量的增加，迭代法变得更为实用，特别是对于那些稀疏矩阵，即大部分元素为零的矩阵，因为迭代法可以更有效地处理这类问题。 克莱姆法则是一种在低维度问题中求解线性方程组的经典方法，它利用系数行列式的逆来直接求得解。然而，随着未知数增多，克莱姆法则的计算复杂度迅速增加，导致在实践中变得不可行。例如，对于20个未知数的线性方程组，即使在高效的计算机上，使用克莱姆法则也可能需要数百年的时间。 误差分析在数值解法中占有重要地位，尤其是在直接法中。由于舍入误差，即使理论上可解的线性方程组在实际计算中也会引入误差。因此，理解解的稳定性、误差传播以及如何选择合适的算法以减小误差至关重要。误差分析可以帮助我们评估解的质量，并指导优化计算策略。 数值分析中的解线性方程组直接法涉及到一系列数学技巧和算法，包括高斯消去、LU分解、平方根法和追赶法等。这些方法各有优劣，需根据问题的具体特性选择合适的方法。同时，迭代法作为另一种策略，提供了解决大规模问题的有效途径，但需要考虑其收敛性问题。在实际应用中，结合误差分析，我们可以找到最经济、最准确的解决方案。