探索概率编程入门与技术应用

需积分: 10 91 浏览量更新于2024-07-18 收藏 3.42MB PDF 举报

《概率编程入门》是一份面向研究生级别的教程，旨在全面介绍概率编程的基础知识及其在设计和构建此类系统中的应用技术。文章适合那些对概率机器学习和编程语言有本科水平理解的读者。作者涵盖了多个领域的专家，包括Jan-Willem van de Meent（Northeastern University）、Brooks Paige（Alan Turing Institute）, Hongseok Yang（KAIST）以及Frank Wood（University of British Columbia），确保了内容的专业性和深度。首先，章节一"模型基础推理"介绍了概率编程背后的逻辑，即如何利用统计模型来处理不确定性问题，通过建模现实世界的复杂性来做出决策。这部分强调了模型在数据分析和决策过程中的核心作用。接着，第二部分"概率编程语言与非递归语法"深入探讨了编程语言如何支持概率模型。讲解了语言的语法结构，如变量定义、概率分布函数和条件语句，同时还引入了"语法糖"的概念，即编程语言中的便利特性，使得表达概率模型更加直观和高效。通过实例演示，读者能更好地理解如何编写实际的程序来描述概率模型。第三章"基于图形的推理"聚焦于将程序编译成图形模型的过程，如概率图模型（PGM）和因子图，以及如何运用这些模型进行密度评估、Gibbs采样（用于近似高维联合分布）和汉明顿蒙特卡洛方法（一种高效的随机抽样算法）。这一部分解释了如何通过图形结构优化计算效率。第四部分"基于评估的推理第一部分"探讨了另一种推理方法，可能涉及变分推断（如期望传播，EP）等技术，这些方法通过优化某个目标函数来估计模型参数，与图形模型方法相辅相成，提供了多元的解决问题途径。《概率编程入门》提供了丰富的理论背景和实践指导，让读者不仅能够掌握概率编程的基本概念，还能了解其实现细节和各种推理技术的优缺点。无论是对初学者还是已经在该领域有一定经验的专业人士，这份文档都是深入了解和应用概率编程不可或缺的参考资料。

1.1. Mo del-based Reasoning 13

Automated model ﬁtting describes the process of using algorithms

to determine either point or distributional estimates for model param-

eters and structure. Such automation is particularly useful when the

parameters of a model are uninterpretable or many. We will return

to model ﬁtting in Chapter 7 however it is important to realize that

inference can be used for model learning too, simply by lifting the

inference problem to include uncertainty about the model itself (e.g. see

the neural network example in 2.3 and the program induction example

in 5.3).

The key point now is to understand that models come in many forms,

from scientiﬁc and engineering simulators in which the results of every

subcomputation are interpretable to abstract models in statistics and

computer science which are, by design, signiﬁcantly less interpretable

but often are valuable for predictive inference none-the-less.

1.1.1 Model Denotation

An interesting thing to think about, and arguably the foundational idea

that led to the ﬁeld of probabilistic programming, is how such models

are denoted and, respectively, how such models are manipulated to

compute quantities of interest.

To see what we mean about model denotation let us ﬁrst look

at a simple statistical model and see how it is denoted. Statistical

models are typically denoted mathematically, subsequently manipulated

algebraically, then “solved” computationally. By “solved” we mean that

an inference problem involving conditioning on the values of a subset of

the variables in the model is answered. Such a model denotation stands

in contrast to simulators which are often denoted in terms of software

source code that is directly executed. This also stands in contrast,

though less so, to generative models in machine learning which usually

take the form of probability distributions whose factorization properties

can be read from diagrams like graphical models or factor graphs.

Nearly the simplest possible model one could write down is a beta-

Bernoulli model for generating a coin ﬂip from a potentially biased coin.

1.1. Mo del-based Reasoning 16

hard, particularly if you think about writing a simulator that only needs

to stochastically generate reasonably plausible scene graphs. Noting

that

(

X, Y

) =

(

Y |X

)

(

) then all we need is a way to go from

scene graph to observable image and we have a complete description of

a joint distribution. There are many kinds of renderers that do just this

and, although deterministic in general, they are perfectly ﬁne to use

when specifying a joint distribution because they map from some latent

scene description to observable pixel space and, with the addition of

some image-level pixel noise reﬂecting, for instance, sensor imperfections

or Monte-Carlo ray-tracing artifacts, form a perfectly valid likelihood.

An example of this “vision as inverse graphics” idea (Kulkarni

et al., 2015b) appearing ﬁrst in Mansinghka et al. (2013) and then

subsequently in Le et al. (2017b,a) took the image

to be a Captcha

image and the scene description

to include the obscured string. In

all three papers the point was not Captcha-breaking per se but instead

demonstrating both that such a model is denotable in a probabilistic

programming language and that such a model can be solved by general

purpose inference.

Let us momentarily consider alternative ways to solve such a “Captcha

problem.” A non-probabilistic programming approach would require

gathering a very large number of Captchas, hand-labeling them all,

then designing and training a neural network to regress from the image

to a text string (Bursztein et al., 2014). The probabilistic program-

ming approach in contrast merely requires one to write a program that

generates Captchas that are stylistically similar to the Captcha family

one would like to break – a model of Captchas – in a probabilistic

programming language. Conditioning such a model on its observable

output, the Captcha image, will yield a posterior distribution over text

strings. This kind of conditioning is what probabilistic programming

evaluators do.

Figure 1.1 shows a representation of the output of such a conditioning

computation. Each Captcha/bar-plot pair consists of a held-out Captcha

image and a truncated marginal posterior distribution over unique string

interpretations. Drawing your attention to the middle of the bottom row,

notice that the noise on the Captcha makes it more-or-less impossible to

tell if the string is “aG8BPY” or “aG8RPY.” The posterior distribution

1.1. Mo del-based Reasoning 17

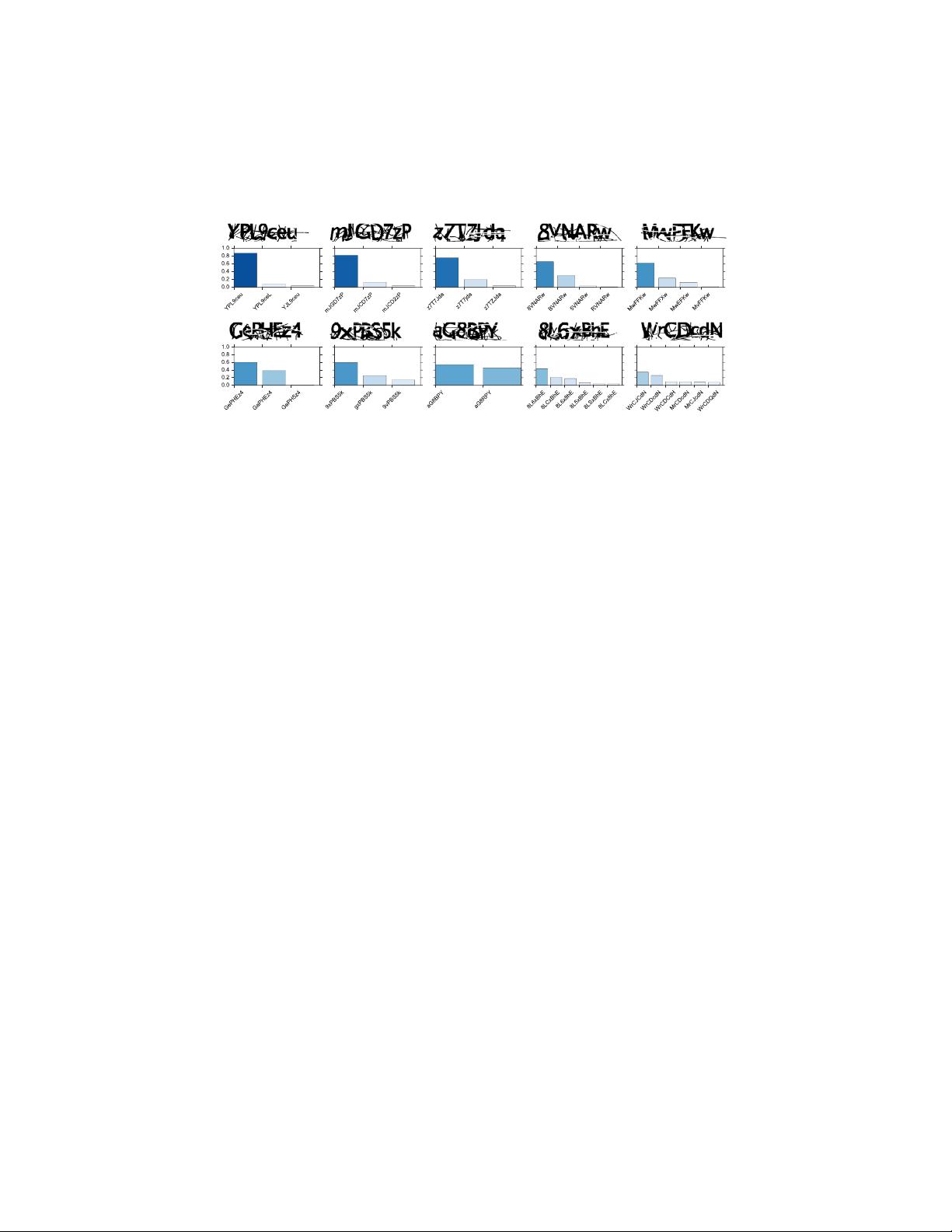
Fig. 4. Posteriors of real Facebook and Wikipedia Captchas. Conditioning on each Captcha, we show an approximate posterior produced by a set of weighted

importance sampling particles {(w

(m)

)}

M=100

m=1

synthetic data generative model sets an empirical cornerstone

for future theory that quantiﬁes and bounds the impact of

model mismatch on neural network and approximate inference

performance.

ACKNOWLEDGMENTS

Tuan Anh Le is supported by EPSRC DTA and Google

(project code DF6700) studentships. Atılım G

unes¸ Baydin and

Frank Wood are supported under DARPA PPAML through

the U.S. AFRL under Cooperative Agreement FA8750-14-2-

0006, Sub Award number 61160290-111668. Robert Zinkov

is supported under DARPA grant FA8750-14-2-0007.

REFERENCES

[1] Y. LeCun, Y. Bengio, and G. Hinton, “Deep learning,”

Nature, vol. 521, no. 7553, pp. 436–444, 2015.

[2] P. Y. Simard, D. Steinkraus, and J. C. Platt, “Best

practices for convolutional neural networks applied to

visual document analysis,” in Proceedings of the Seventh

International Conference on Document Analysis and

Recognition - Volume 2, ser. ICDAR ’03. Washington,

DC: IEEE Computer Society, 2003, pp. 958–962.

[3] A. Krizhevsky, I. Sutskever, and G. E. Hinton, “Imagenet

classiﬁcation with deep convolutional neural networks,”

in Advances in Neural Information Processing Systems,

2012, pp. 1097–1105.

[4] M. Jaderberg, K. Simonyan, A. Vedaldi, and A. Zis-

serman, “Synthetic data and artiﬁcial neural networks

for natural scene text recognition,” arXiv preprint

arXiv:1406.2227, 2014.

[5] ——, “Reading text in the wild with convolutional neural

networks,” International Journal of Computer Vision,

vol. 116, no. 1, pp. 1–20, 2016.

[6] A. Gupta, A. Vedaldi, and A. Zisserman, “Synthetic Data

for Text Localisation in Natural Images,” in Proceedings

Figure 1.1:

Posterior uncertainties after inference in a probabilistic programming

language model of 2017 Facebook Captchas (reproduced from Le et al. (2017a))

P (X|Y ) arrived at by conditioning reﬂects this uncertainty.

By this simple example, whose source code appears in Chapter 5 in

a simpliﬁed form, we aim only to liberate your thinking in regards to

what a model is (a joint distribution, potentially over richly structured

objects, produced by adding stochastic choice to normal computer pro-

grams like Captcha generators) and what the output of a conditioning

computation can be like. What probabilistic programming languages

do is to allow denotation of any such model. What this tutorial cov-

ers in great detail is how to develop inference algorithms that allow

computational characterization of the posterior distribution of interest,

increasingly very rapidly as well (see Chapter 7).

1.1.2 Conditioning

Returning to our simple coin-ﬂip statistics example, let us continue and

write out the joint probability density for the distribution on

and

The reason to do this is to paint a picture, by this simple example, of

what the mathematical operations involved in conditioning are like and

why the problem of conditioning is, in general, hard.

Assume that the symbol

denotes the observed outcome of the

coin ﬂip and that we encode the event “comes up heads” using the

mathematical value of the integer 1 and 0 for the converse. We will

denote the bias of the coin, i.e. the probability it comes up heads, using

剩余217页未读，继续阅读

CSean

粉丝: 0
资源: 6

探索概率编程入门与技术应用

an introduction to probabilistic graphical models by Michael Jordan

An introduction to probabilistic graphical models

An Introduction to Probabilistic Graphical Models

Introduction to Probabilistic Modelling

Introduction to Probabilistic Graphical Models

Introduction to Probabilistic Graphical Models_M.I.Jordan_2003.pdf

Probabilistic Networks — An Introduction to Bayesian Networks and Influence Diagrams

Probabilistic Machine Learning-An Introduction

An Introduction to Information Retrieval 信息检索lucene

An Introduction to Cryptography - 2nd Edition - 2007

最新资源