滤波反投影原理详解：基于傅里叶切片定理与图像重建

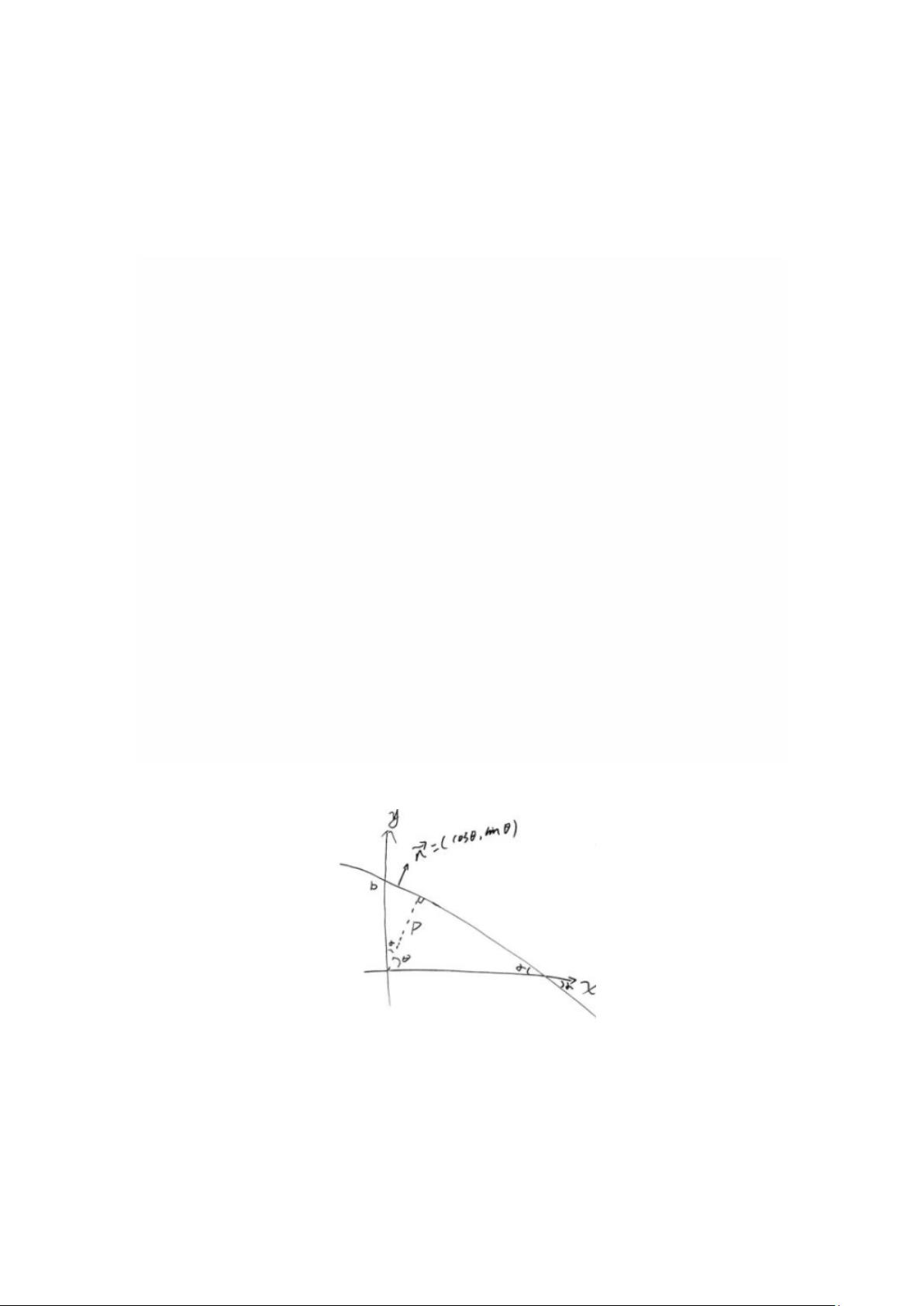
FBP总结1深入探讨了在医学成像中的滤波反投影技术，这是一种在计算机断层扫描（CT）等成像技术中广泛应用的方法。首先，理解朗伯比尔定律对于图像衰减系数的测量至关重要，它揭示了物质对光的不同吸收特性与像素值之间的关系。 投影过程分为正投影和反投影。正投影通过沿特定角度对图像进行线积分，计算出对应的权值，形成二维数据集的 Radon 变换。反投影则利用这些权值，通过逆过程恢复原始图像。在这个过程中，投影角（非与x轴夹角）和径向坐标（xp）起着关键作用。 Radon变换是一种将二维图像映射到一维直线参数的工具，其离散版本用于CT扫描中的重建。通过傅里叶切片定理，我们了解到一维傅里叶变换与二维傅里叶变换之间的联系：投影的一维傅里叶变换可以视为二维区域的二维傅里叶变换在特定角度的切片。 滤波反投影公式推导涉及将图像从频率域转换回空间域的过程。利用傅里叶切片定理，将反傅里叶变换转换为极坐标形式，通过二重积分进行计算。滤波器的选择在此过程中非常重要，因为适当的滤波器可以减少图像模糊问题，提升重建图像的质量，如使用低通滤波器进行平滑处理。 FBP总结1详细解释了从物理原理到数学模型的各个环节，包括衰减系数的测量、投影与反投影操作、Radon变换的应用以及如何利用傅里叶切片定理实现滤波反投影，这些都是确保图像重建质量的关键步骤。理解并掌握这些概念和技术，对于图像处理和医学成像领域的专业人士来说是必不可少的基础知识。