有限元法基础与三角形单元解析

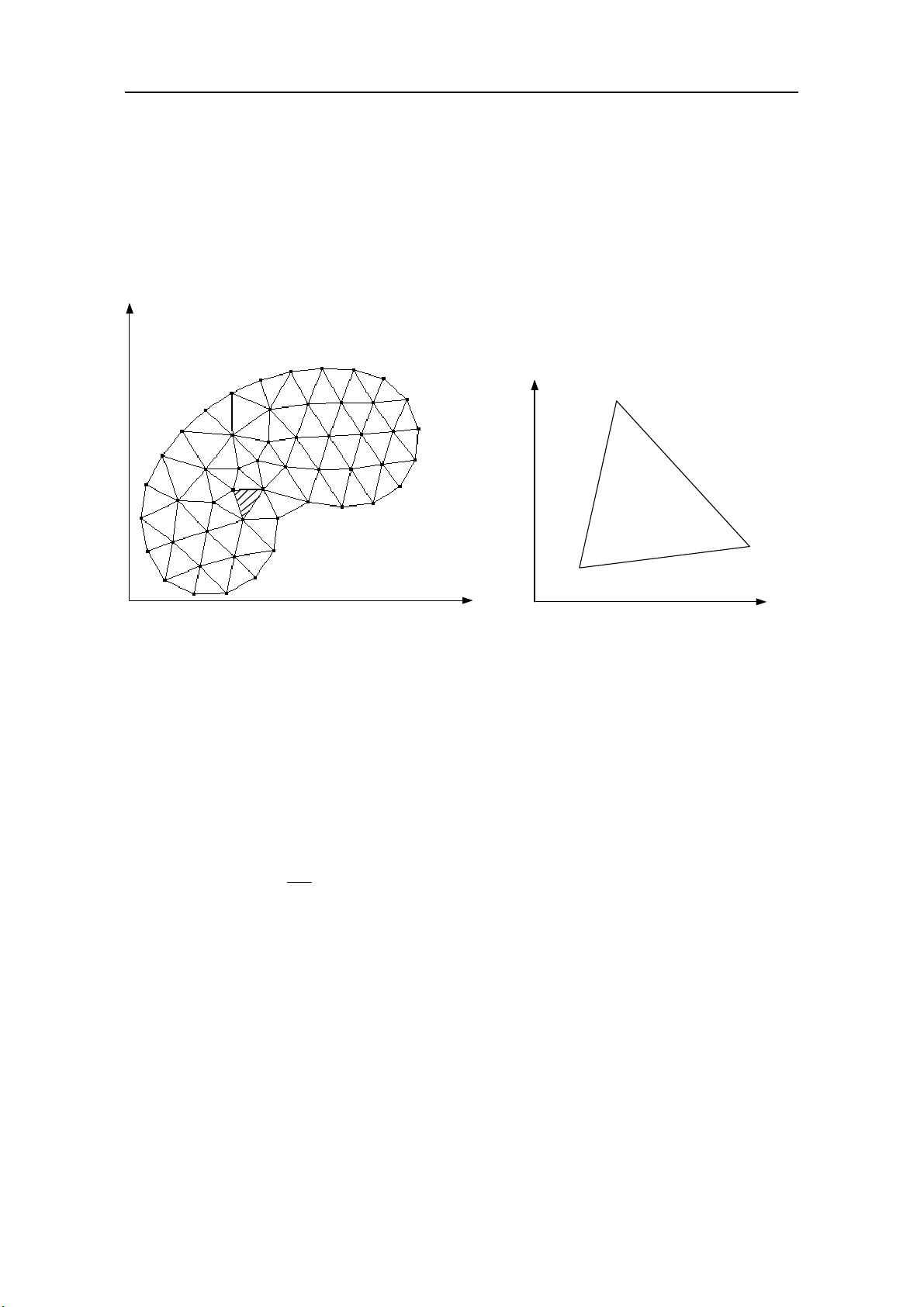
"有限元法基本理论讲义涵盖了有限元法的基础知识，旨在帮助学习者快速理解这一计算方法。内容包括三角形有限元法的求解过程，位移函数的设定，以及单元的应力应变矩阵等核心概念。" 有限元法是一种数值分析方法，广泛应用于工程领域的结构分析、流体力学、热传导等问题。在这个讲义中，主要讨论的是二维三角形有限元的求解步骤和理论基础。 首先，讲义介绍了三角形单元的位移函数假设。在离散化的二维域Ω中，三角形单元通过结点编码m, j, i进行标识，并规定了逆时针编码为正向。位移函数u和v分别在x和y方向的表达式由插值函数或形函数Ni定义，这些形函数是基于节点坐标构建的多项式函数。形函数Ni的定义式（1.3）中，a, b, c是节点坐标，N是基函数，i, j, m是节点编号。接着，形函数的性质通过（1.4）式表达，它展示了形函数下标轮换的规则。 位移函数的线性组合（1.5）式简洁地表示了单元内的位移场，这是有限元法中关键的一环。式（1.6）进一步给出了单元内部位移向量与节点位移之间的关系，即形函数矩阵N的乘积。 在有限元法中，单元的应力应变矩阵B至关重要，因为它连接了几何方程和物理方程。形函数的偏导数构成的B矩阵（1.8）描述了应变与位移的关系，而通过（1.9）式，我们可以得到与材料常数A有关的B矩阵的具体形式。 一旦求得了单元的应力应变矩阵，就可以将其代入到物理方程（如胡克定律）中，以求解单元内部的应力分布。在连续体中，所有单元的贡献组合起来，就构成了整个问题的解。这种方法的优点在于，即使面对复杂几何形状和非线性问题，也能通过离散化处理转化为可求解的数学模型。 总结来说，这个讲义详细阐述了有限元法的核心概念，包括三角形单元的位移函数定义、形函数的性质、单元的应力应变矩阵的建立，这些都是理解有限元法并应用其解决实际问题的基础。学习者通过这些理论可以逐步掌握如何运用有限元法来模拟和分析各种工程问题。