快速傅里叶变换算法详解与优化策略

快速傅里叶变换（Fast Fourier Transform, FFT）是一种高效的信号处理算法，用于计算离散信号的频域表示，其核心在于大幅减少了计算DFT（离散傅里叶变换）所需的时间复杂度。本文主要介绍了快速傅里叶变换的几个关键概念和技术。 首先，引言部分回顾了快速傅里叶变换的历史，包括库利和图基提出的早期算法以及桑德和图基开发的快速算法。文章着重讨论了几种主要的FFT算法，这些算法在实际应用中具有重要意义。 直接计算DFT时，存在明显的效率问题，因为它的计算量与序列长度的平方成正比，即需要执行4次行乘法和N^2次加法操作。这种计算量对于长序列来说是巨大的。为了减少工作量，人们利用了DFT的一些性质，如： 1. **对称性**：序列中的某些项是彼此镜像对称的，这意味着在计算过程中可以避免重复处理，从而减少乘法和加法次数。 2. **周期性**：DFT中的N点DFT实际上是对一个周期函数进行的计算，可以通过周期性来简化计算。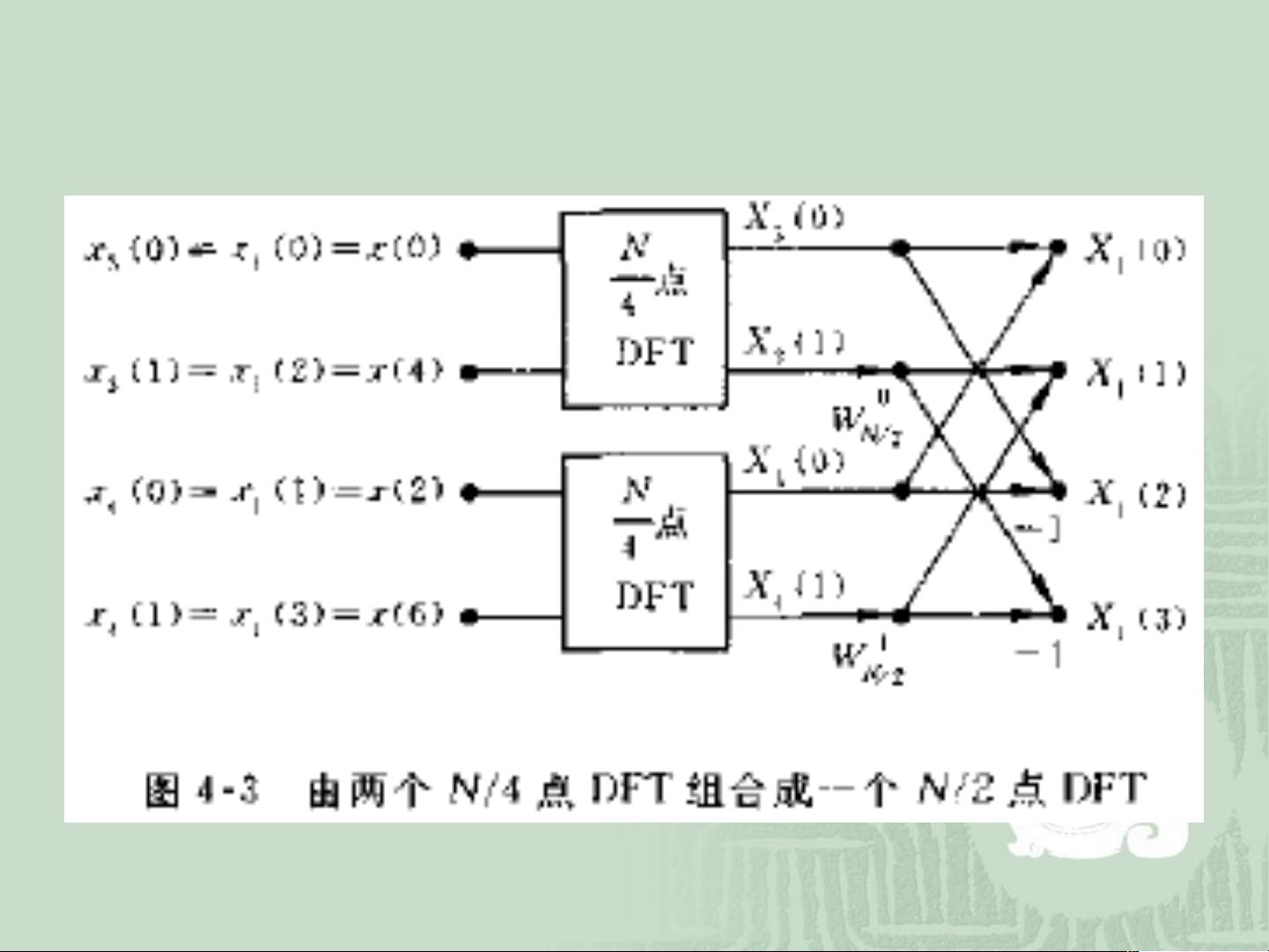 3. **可约性**：当序列可以被2整除时，可以通过分解为两个长度为N/2的子序列，然后分别计算再组合，进一步降低计算复杂度。 按时间抽选的基-2FFT算法，也称为Cooley-Tukey算法，是FFT最著名的实现之一。该算法的基本思想是将原序列分为两部分，利用系数的可约性，将长序列的DFT分解为两个长度为N/2的子序列的DFT。通过递归应用此过程，直到序列长度为1，最终只需要O(N log N)的计算复杂度，大大降低了计算工作量。 该算法的具体步骤如下： - 将序列分为奇数和偶数索引部分。 - 将每个部分分别进行DFT，然后通过复数乘法结合得到完整的DFT结果。 - 这个过程可以写作一个递归公式，例如，对于序列长度N=2L，可以表示为\( X_k = \sum_{n=0}^{L-1} x_{2n}W^{kn} + \sum_{n=0}^{L-1} x_{2n+1}W^{(2k+1)n} \)。 - 式中，\( W = e^{-j\frac{2\pi}{N}} \) 是DFT的基波，\( k \) 和 \( n \) 分别是频率和时间索引。 此外，文中还提到了其他类型的FFT算法，如针对N为复合数的混合基算法，线性调频Z变换（Chirp-z变换）算法，以及如何用FFT加速线性卷积和线性相关计算。这些算法都是在不同应用场景下优化DFT性能的重要工具。 快速傅里叶变换是信号处理领域中的基石，它通过巧妙地利用数学特性，实现了对复杂信号高效分析和处理的能力，对通信、图像处理、音频处理等多个领域都有深远影响。