数值方法课程设计：线性方程组解法比较与分析

"该资源包含了多个数值方法课程设计题目，主要涉及线性方程组的解法，包括但不限于Gauss消去法（不选主元、列主元、完全主元）、平方根法和追赶法。题目要求用计算机语言编写程序解决特定的线性方程组，并对不同方法的适用性和计算结果进行比较分析。" 在数值计算领域，解线性方程组是基础且重要的任务。Gauss消去法是一种常用的方法，它通过一系列行变换将系数矩阵转化为上三角或下三角形式，进而求解。在这个课程设计中，学生需要实现不选主元、列主元和完全主元的Gauss消去法。不选主元方法简单但可能不稳定，列主元和完全主元方法则能有效提高算法的稳定性，特别是对于系数矩阵中的大元素或接近零的元素。 第一部分的题目要求求解特定的线性方程组，学生需利用自己熟悉的编程语言（如Python、C++或Matlab）实现上述三种Gauss消去法，并对比它们的计算结果。此外，学生还应探讨其他可能的解法，例如高斯-约旦消去法、LU分解、QR分解等，并选择其中的一些方法进行编程求解，以确定哪种方法最适合特定的线性方程组。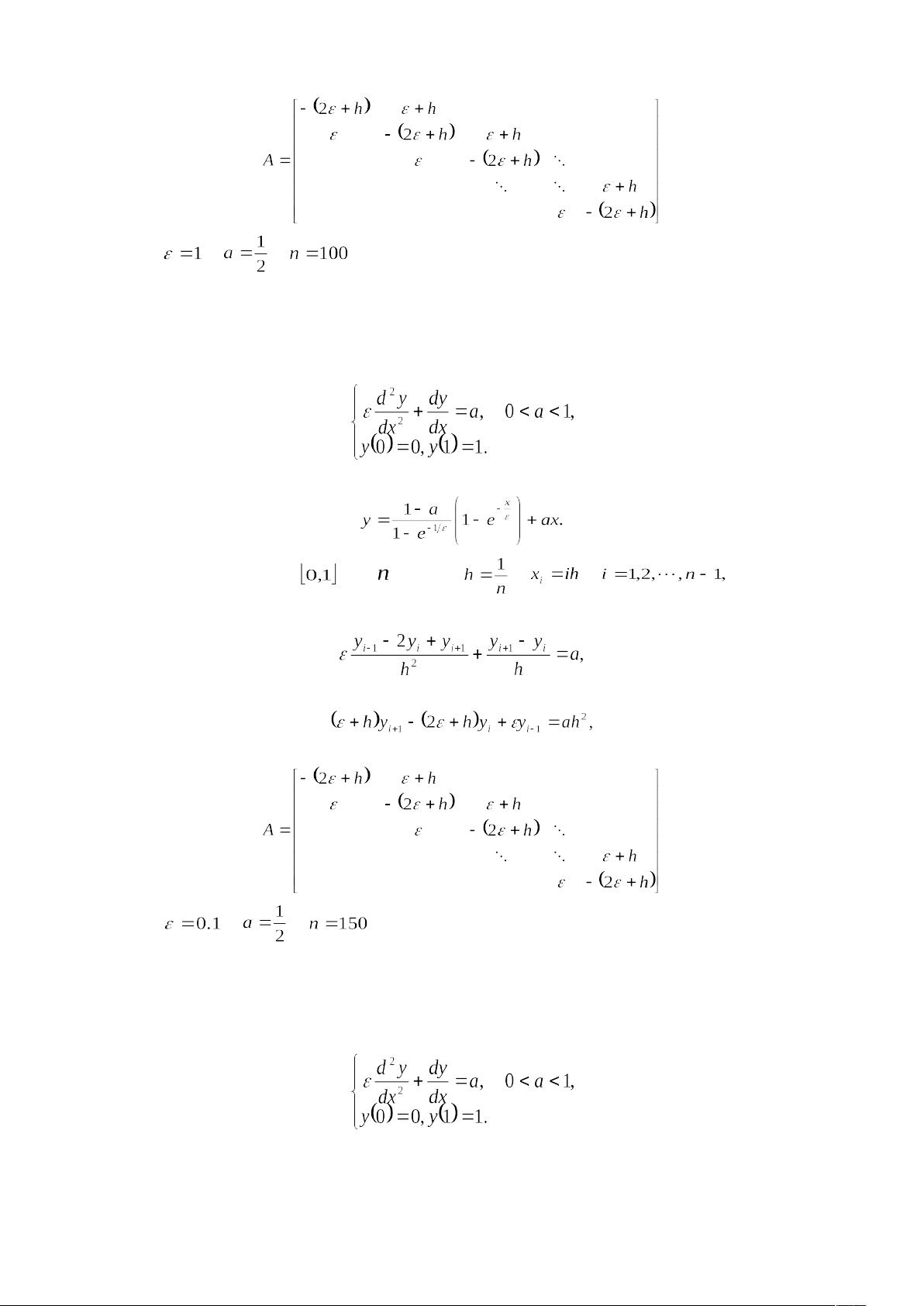 平方根法和追赶法是另一种解线性方程组的方法，特别适用于对称正定的矩阵。在第二部分的题目中，学生需要实现这两种方法，处理随机生成的100阶和150阶对称正定矩阵。同样，他们需要比较不同方法的效率和准确性，并给出自己的见解。 第三和第四部分的题目引入了Hilbert矩阵，这是一种特殊的系数矩阵，其元素具有特定的递归关系，导致系统通常高度病态。求解这类问题通常需要更高级的方法，如迭代法（如CG、GMRES）或预条件技术。学生需要编写程序解决50阶和100阶的Hilbert矩阵线性方程组，至少使用三种不同的方法，并对结果进行精度分析。通过改变矩阵的阶数，可以探讨精度与计算复杂度之间的关系。 这个课程设计涵盖了数值线性代数中的多种基本方法，旨在训练学生的编程能力和对算法性能的理解。完成这些题目将帮助学生深入掌握线性方程组的数值解法，并能够根据具体问题选择最适宜的求解策略。