x
1
x
2
x
4
x
3
x
8
x
5
x
6
x
7
New Seg ment
x
12
x
9
x
10
x
11
Fixed (No Grad)
x
1
x
2
x
4
x
3
x
8
x
5
x
6
x
7
Fixed (No Grad) New Seg ment
(a) Training phase.
x
1
x
2
x
4
x
3
x
8
x
5
x
6
x
7
x
12
x
9
x
10
x
11
Extende d Co ntext
(b) Evaluation phase.
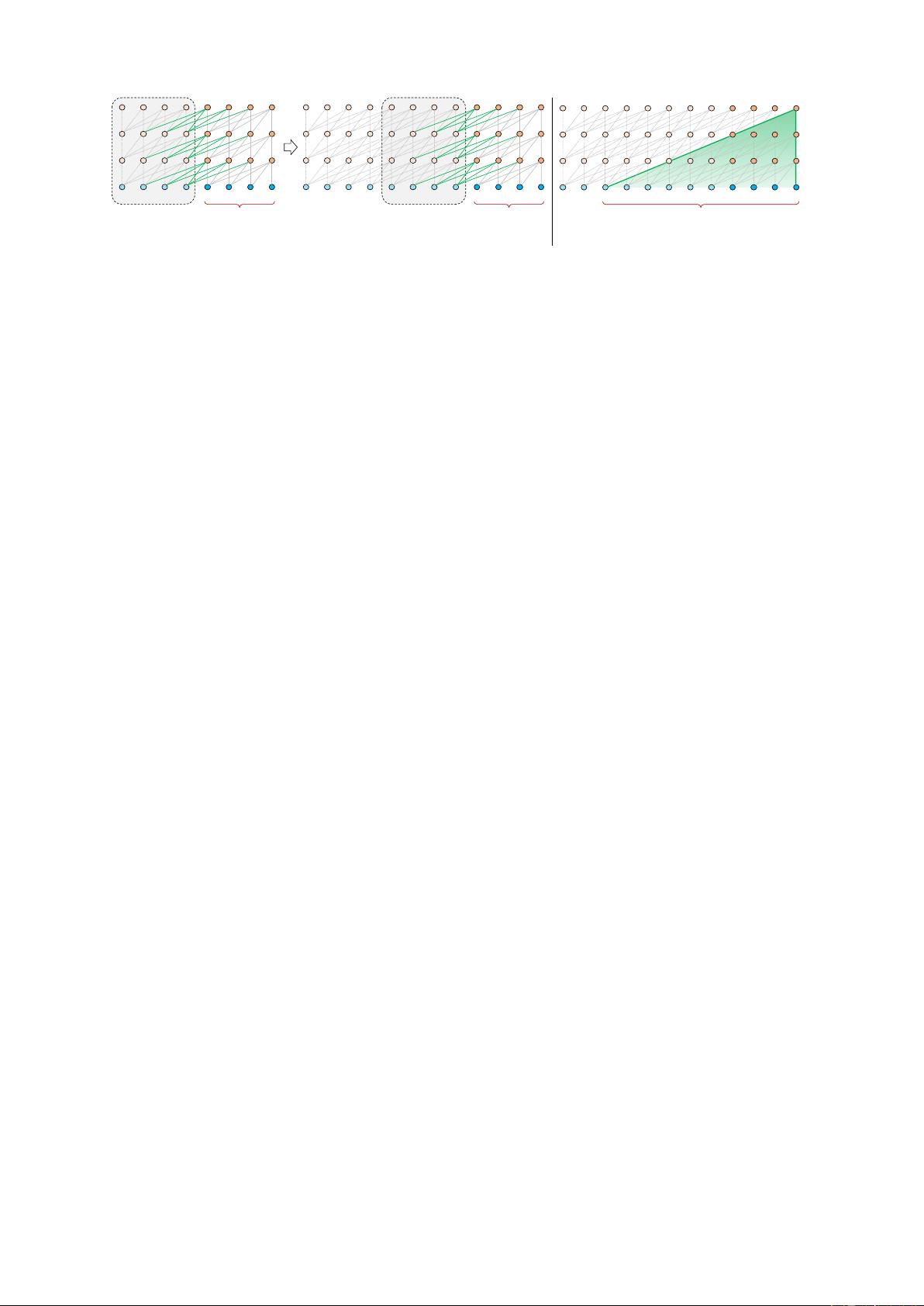
Figure 2: Illustration of the Transformer-XL model with a segment length 4.
per-segment, which differs from the same-layer
recurrence in conventional RNN-LMs. Conse-
quently, the largest possible dependency length
grows linearly w.r.t. the number of layers as well
as the segment length, i.e., O(N × L), as vi-
sualized by the shaded area in Fig. 2b. This
is analogous to truncated BPTT (Mikolov et al.,
2010), a technique developed for training RNN-
LMs. However, different from truncated BPTT,
our method caches a sequence of hidden states in-
stead of the last one, and should be applied to-
gether with the relative positional encoding tech-
nique described in Section 3.3.
Besides achieving extra long context and re-
solving fragmentation, another benefit that comes
with the recurrence scheme is significantly faster
evaluation. Specifically, during evaluation, the
representations from the previous segments can
be reused instead of being computed from scratch
as in the case of the vanilla model. In our ex-
periments on enwiki8, Transformer-XL is up to
1,800+ times faster than the vanilla model during
evaluation (see Section 4).
Finally, notice that the recurrence scheme does
not need to be restricted to only the previous seg-
ment. In theory, we can cache as many previous
segments as the GPU memory allows, and reuse
all of them as the extra context when processing
the current segment. Thus, we can cache a prede-
fined length-M old hidden states spanning (pos-
sibly) multiple segments, and refer to them as the
memory m
n
τ
∈ R
M×d
, due to a clear connection to
the memory augmented neural networks (Graves
et al., 2014; Weston et al., 2014). In our experi-
ments, we set M equal to the segment length dur-
ing training, and increase it by multiple times dur-
ing evaluation.
3.3 Relative Positional Encodings
While we found the idea presented in the pre-
vious subsection very appealing, there is a cru-
cial technical challenge we haven’t solved in or-
der to reuse the hidden states. That is, how can
we keep the positional information coherent when
we reuse the states? Recall that, in the standard
Transformer, the information of sequence order is
provided by a set of positional encodings, denoted
as U ∈ R
L
max
×d
, where the i-th row U
i
corre-
sponds to the i-th absolute position within a seg-
ment and L
max
prescribes the maximum possible
length to be modeled. Then, the actual input to the
Transformer is the element-wise addition of the
word embeddings and the positional encodings. If
we simply adapt this positional encoding to our
recurrence mechanism, the hidden state sequence
would be computed schematically by
h
τ +1
= f (h
τ
, E
s
τ +1
+ U
1:L
)
h
τ
= f (h
τ −1
, E
s
τ
+ U
1:L
),
where E
s
τ
∈ R
L×d
is the word embedding se-
quence of s
τ
, and f represents a transformation
function. Notice that, both E
s
τ
and E
s
τ +1
are as-
sociated with the same positional encoding U
1:L
.
As a result, the model has no information to dis-
tinguish the positional difference between x
τ,j
and
x
τ +1,j
for any j = 1, . . . , L, resulting in a sheer
performance loss.
In order to avoid this failure mode, the funda-
mental idea is to only encode the relative posi-
tional information in the hidden states. Concep-
tually, the positional encoding gives the model a
temporal clue or “bias” about how information
should be gathered, i.e., where to attend. For the
same purpose, instead of incorporating bias stati-
cally into the initial embedding, one can inject the
same information into the attention score of each
layer. More importantly, it is more intuitive and
generalizable to define the temporal bias in a rela-
tive manner. For instance, when a query vector q
τ,i
attends on the key vectors k
τ,≤i
, it does not need
to know the absolute position of each key vector
to identify the temporal order of the segment. In-
stead, it suffices to know the relative distance be-
tween each key vector k
τ,j
and itself q
τ,i
, i.e. i−j.
Practically, one can create a set of relative posi-









