离散结构算法解析：线段树与树状数组在动态统计问题中的应用

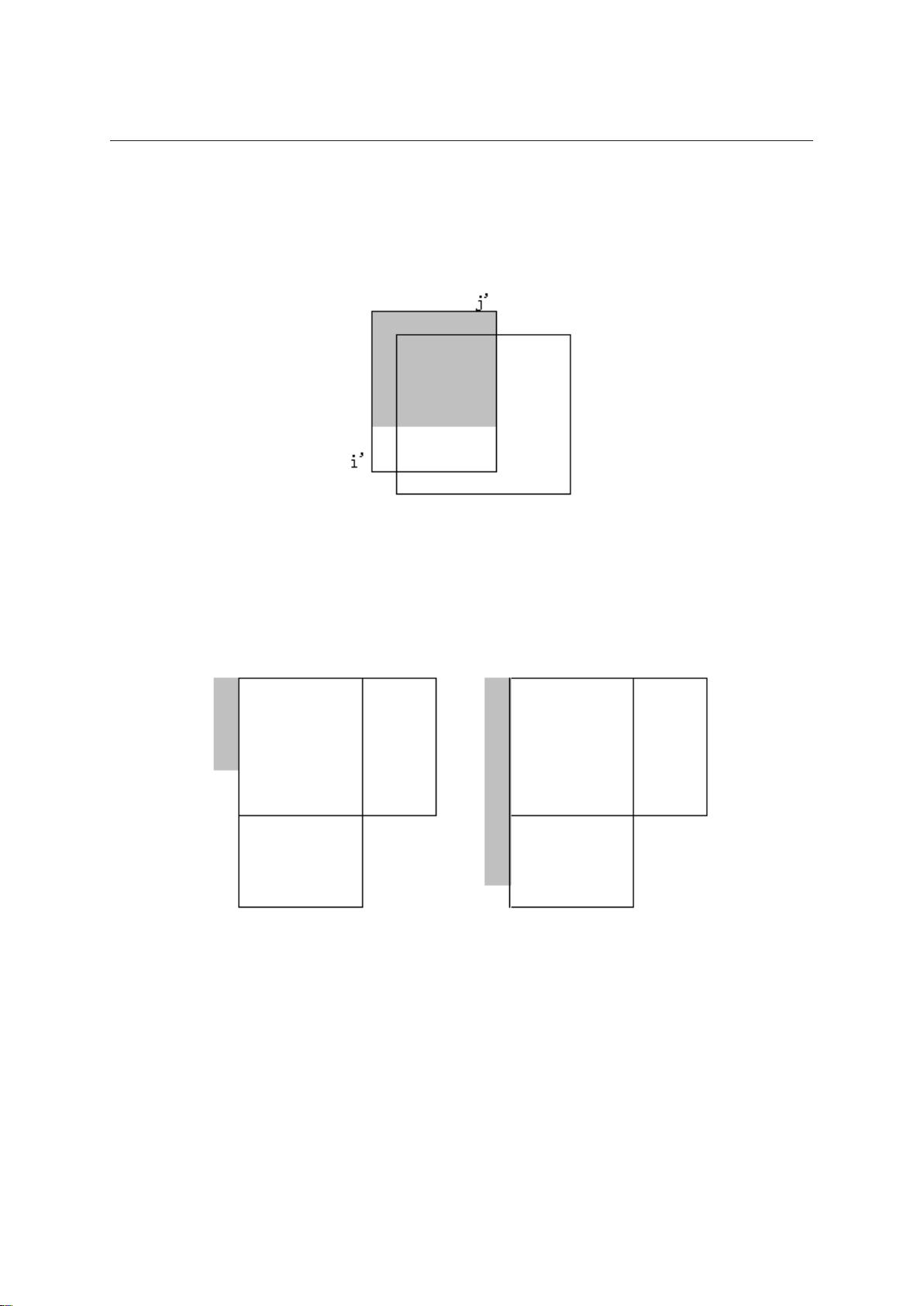
"《算法艺术与信息学竞赛》学习指导(下).pdf" 在《算法艺术与信息学竞赛》学习指导(下)中，第六章详细探讨了离散结构上的算法，特别是针对序列、树、图和字符串等离散结构的算法设计。这一章的焦点在于如何利用这些结构的特性来解决实际问题。 6.1节专注于序列上的问题，讲解了一系列在序列数据上的算法。序列是最基本的离散结构之一，尽管看似简单，但可以衍生出许多高效的算法。在这个部分，作者特别提到了线段树和树状数组这两种重要的数据结构。 线段树是一种特殊的数据结构，常用于处理区间或线性范围上的动态问题。线段树通过将区间不断二分形成树形结构，反映了许多分治算法的思路。如图8.1所示，线段树能够将区间[1,10]划分为单个点，并具备以下特性： 1. 每一层都是区间[a, b]的一个划分，长度为L = b - a。 2. 总共有log2L层。 3. 对于任何点p，从根节点到叶节点p的路径上的区间都包含点p，而其他区间不包含。 4. 给定区间[l, r]，可以将其分解为不超过2log2L个不相交的子区间。 线段树的优势在于，对于点的修改和区间统计，都可以在O(logL)的时间复杂度内完成。修改一个点只需要更新log2L个树中区间的信息，而统计区间和只需累加2log2L个树中区间的信息。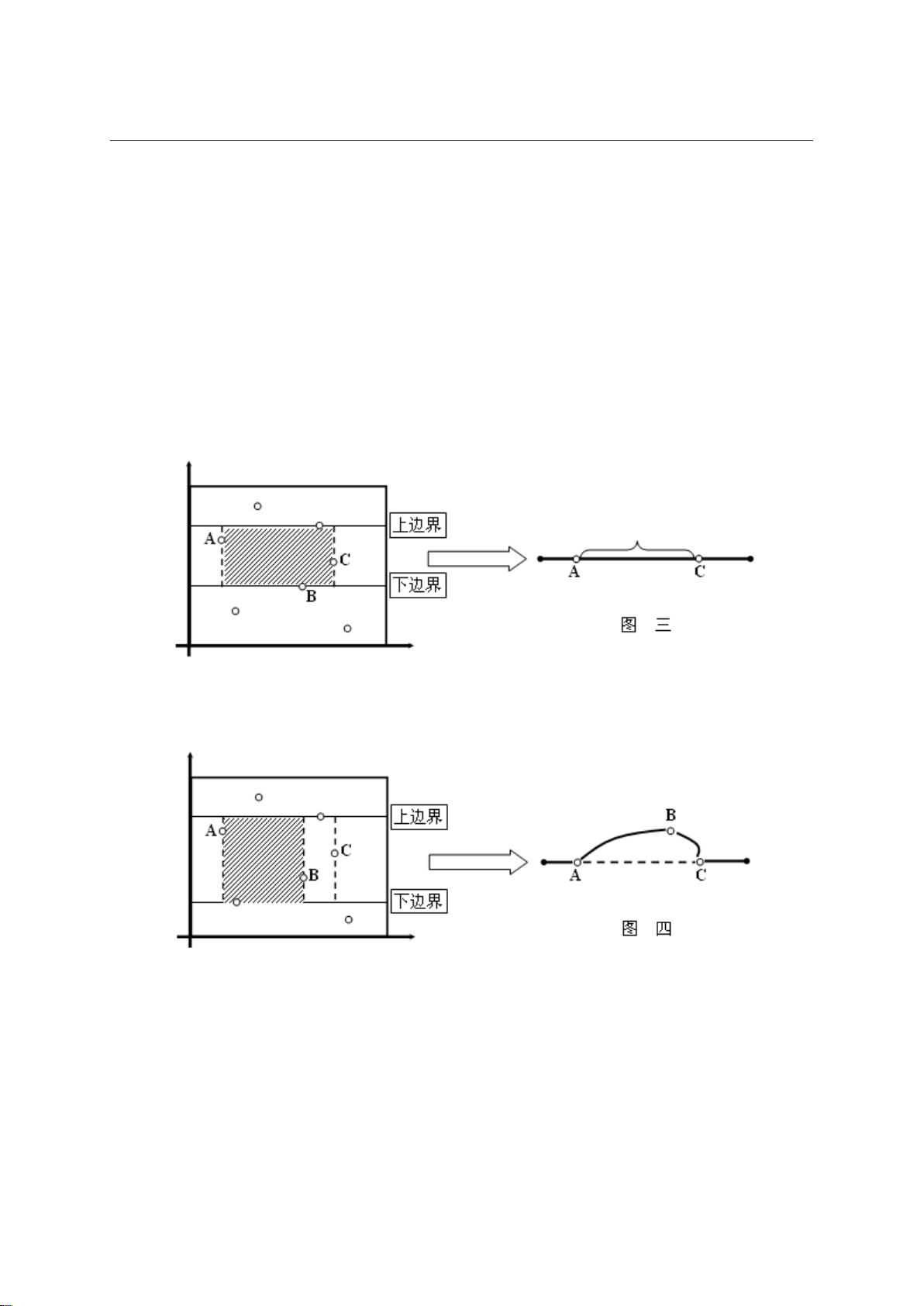 接着，书中通过两个动态统计问题展示了线段树的实际应用。第一个问题是数组A的动态统计，其中允许修改单个元素和查询区间和。直接操作的方法时间复杂度可能达到O(n)，而采用线段树则能将修改和查询操作的时间复杂度降低到O(logn)。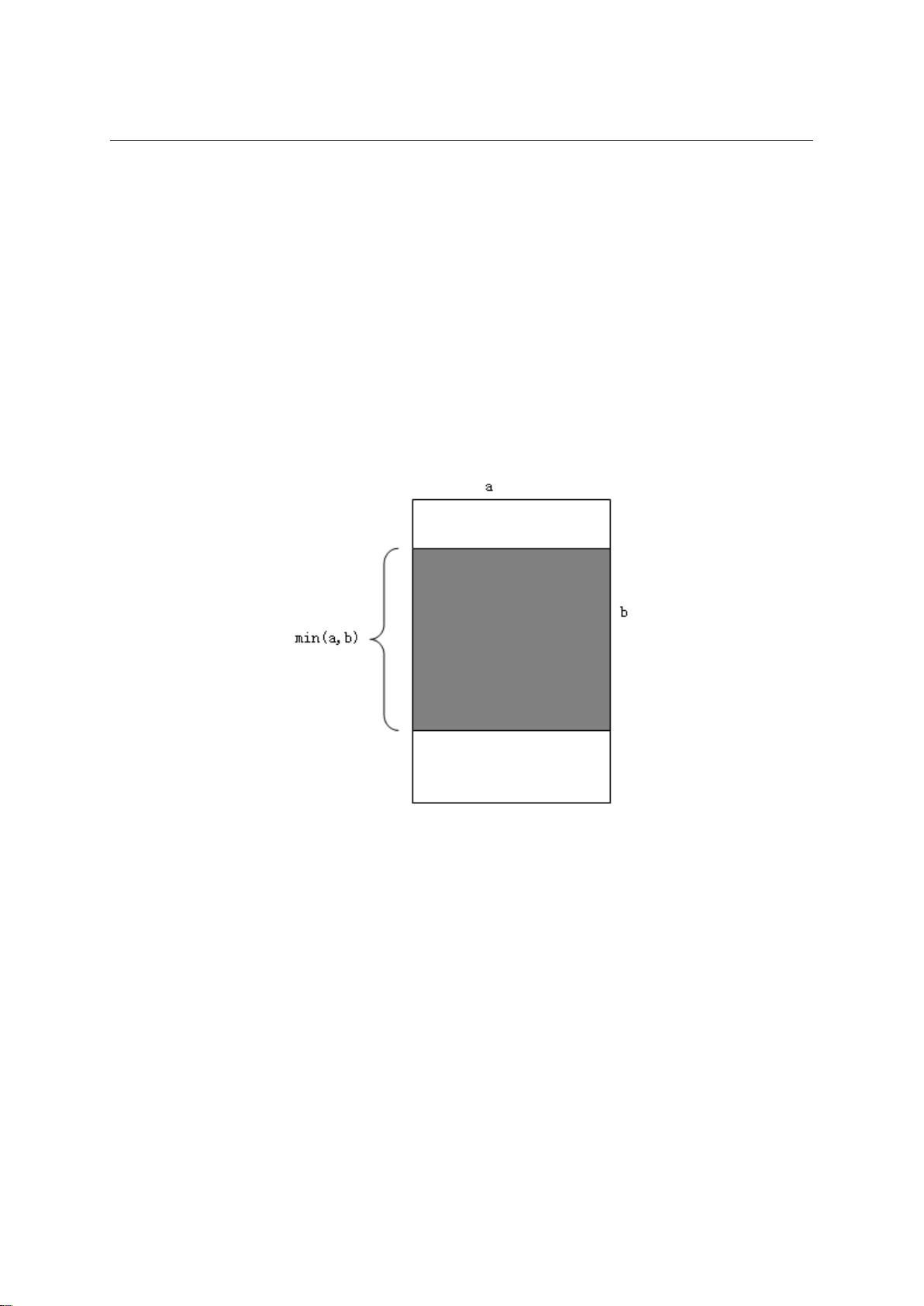 第二个动态统计问题扩展了第一个问题，允许对一个区间内的所有元素同时增加一个数d。同样，线段树在这里发挥了关键作用，优化了操作的时间复杂度。 通过这两个问题，我们可以看出，理解和掌握线段树这种数据结构对于解决动态统计类问题至关重要，它能够有效地减少操作的时间复杂度，提高算法效率。在信息学竞赛和实际编程中，这样的高效算法是解决问题的关键工具。